Лекция№10

Лекция №10

Графический метод решения ЗЛП

Рассмотрим ЗЛП в канонической форме: .

Пусть - ненулевой вектор, тогда линейная форма задачи задает в пространстве семейство параллельных гиперплоскостей линейной формы , нормальным вектором которых является вектор C. Если - фиксированное значение, то гиперплоскость делит все пространство на два полупространства: нижнее и верхнее .

Если существует : , то - оптимальный опорный план. Гиперплоскость - опорная гиперплоскость множества М в точке . Причем по отношению к опорной гиперплоскости все множество М находится в нижнем полупространстве, т.к. . Поэтому для графического решения задачи необходимо найти опорную гиперплоскость, по отношению к которой все множество М находится в нижнем полупространстве.

Таким образом, графический метод решения ЗЛП заключается в перемещении гиперплоскости линейной формы из некоторого начального положения по направлению вектора С до такого положения, когда при дальнейшем смещении гиперплоскость уже не будет иметь общих с множеством М точек. Пересечение опорной гиперплоскости с множеством М и будет является решением ЗЛП.

Для того чтобы решить графически ЗЛП необходимо выполнить следующие действия.

1. Построить множество допустимых планов задачи. В общем случае оно представляет собой выпуклый многогранник. Если ограничения в задаче несовместны, множество допустимых планов является пустым множеством, а задача поиска экстремума не имеет смысла.

2. Построить вектор С с началом в некоторой точке .

3. Построить гиперплоскость линейной формы (линию уровня) проходящую через точку .

4. Передвигать гиперплоскость линейной формы параллельно самой себе в направлении вектора C (так как вектор задает направление возрастания F(X)) до получения опорной гиперплоскости.

Замечание. В случае непустого множества допустимых планов возможны три типовых ситуации:

а) опорная гиперплоскость касается множества допустимых планов в одной точке (задача имеет единственное решение);

б) опорная гиперплоскость касается множества допустимых планов вдоль стороны многоугольника (задача имеет бесконечное множество решений);

в) опорная гиперплоскость не определяется (задача не имеет решения).

Пример 10.1. Решить графически двумерную задачу линейного программирования:

1. Легко проверить, что четырехугольник на рис 10.1 является областью содержащей точки, для которых выполнены все ограничения задачи. Точки, лежащие внутри и на границе этой области являются допустимыми планами.

2. Построим вектор , с началом в некоторой точке D с координатами (100; 100). Очевидно, что вектор С, в силу линейности функции будет перпендикулярен линиям уровня.

3. Построим линию уровня, проходящую через выбранную точку D. Подставим координаты точки D в целевую функцию : . Уравнение линии уровня, соответствующей данному значению будет иметь следующий вид . Построим полученную прямую (на рис.10.1 она обозначена (3')).

Рис.10.1.

4. Перемещая гиперплоскость линейной формы (линию уровня) из начального положения по направлению вектора С находим крайнее положение, определяющее опорную гиперплоскость. Поскольку полученная нами опорная гиперплоскость пересекается с множеством М в точке В, то наша задача имеет единственное решение.

Точка расположена на пересечении двух прямых (1') и (2'), поэтому, чтобы найти ее координаты необходимо решить следующую систему уравнений:

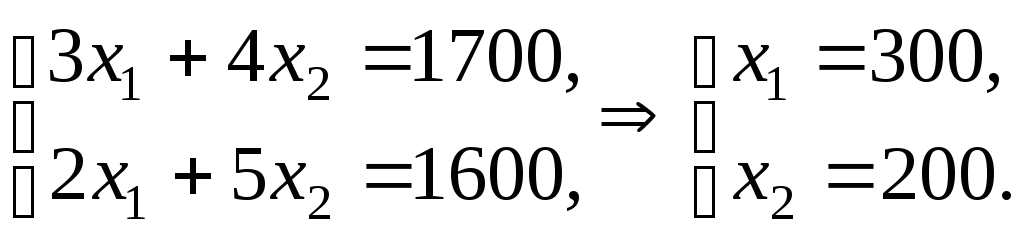
Таким образом - точка, соответствующая оптимальному решению задачи со значением функции .

Пример 10.2. Решим графически двумерную задачу линейного программирования:

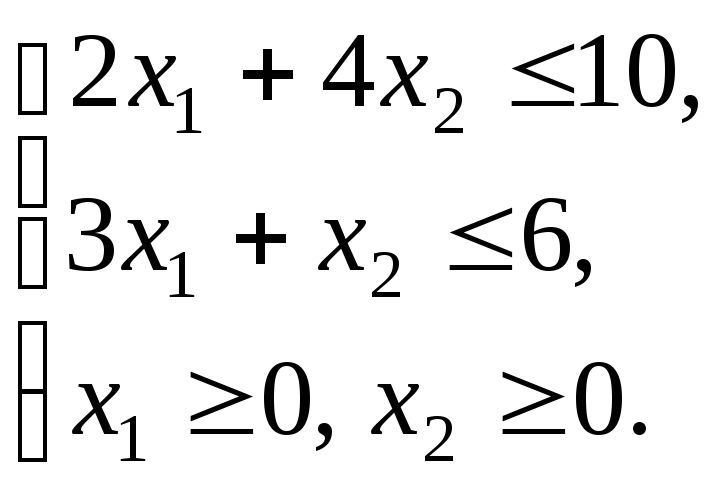
1. Окрашенная область ОАВС на рис.10.2 – множество допустимых планов ЗЛП.

2. Построим вектор С с началом в точке принадлежащей множеству допустимых планов, например, в точке D с координатами (1; 1).

3. Уравнение линии уровня проходящей через точку D будет иметь вид: . Построим полученную прямую (на рис.10.2 она обозначена (3')).

Рис 10.2.

4. Перемещая гиперплоскость линейной формы (линию уровня) из начального положения (3') по направлению вектора С находим крайнее положение, определяющее опорную гиперплоскость. Поскольку полученная нами гиперплоскость пересекается с множеством М по ребру АВ, то наша задача имеет бесконечное множество решений. А именно, все точки отрезка АВ являются оптимальными планами задачи, на которых достигается максимальное значение линейной формы .

Метод последовательного улучшения плана

Метод основан на упорядоченном переборе угловых точек множества планов задачи в сторону увеличения (или уменьшения) линейной формы и содержит три существенных момента.

Во-первых, указывается способ вычисления опорного плана. Во-вторых, устанавливается, признак, который позволяет проверить, является ли выбранный опорный план оптимальным. В третьих приводится способ, позволяющий по выбранному неоптимальному опорному плану построить другой опорный план, более близкий к оптимальному.

Переход от одного опорного плана к другому опорному плану

Рассмотрим ЗЛП в канонической форме

, (10.1)

где - матрица условий размером

Пусть ранг матрицы условий равен . Пусть все опорные планы задачи являются невырожденными и - произвольный опорный план с базисом . Т.е. считаем первые компонент точки положительными. Так как точка принадлежит , то ее координаты удовлетворяют системе ограничений

. (10.2)

Так как вектора составляющие базис - линейно независимы, то существуют не все равные нулю, такие что

Разложим вектор по базису .

(10.3)

Умножим обе части последнего соотношения на некоторую величину , и результат вычтем из (10.2)

. (10.4)

Отсюда следует, что точка

удовлетворяет ограничениям типа равенств задачи (10.1). Чтобы эта точка являлась планом задачи необходимо выполнение условий неотрицательности её координат

(10.5)

При этом,

• если все , то (10.5) выполняется при любом

• если же существует , то (10.5) будет выполняться не при любом значении .

Решая неравенства относительно , получим

.

Ясно что, таких чисел может быть больше одного. Выберем наименьшее из них и обозначим его , т.е.

.

Так как план невырожденный и следовательно, , то . Итак, чтобы точка принадлежала множеству планов ЗЛП , нужно брать из полуинтервала . Однако при точка содержит положительных координат и, следовательно, не является угловой. План может быть опорным лишь при таком , при котором одна из его компонент обратиться в ноль. Очевидно, это произойдет при .

Пусть для определенности

Тогда первая координата обратиться в ноль

,

т.е. имеет ровно положительных координат.

Покажем, что - опорный план ЗЛП. Для этого нужно показать, что столбцы образуют линейно – независимую систему векторов.

Допустим противное, т.е., что вектора - линейно зависимы. Тогда существует

. (10.6)

С другой стороны, мы уже знаем, что

(10.7)

Подставим выражение (10.7) в предыдущее равенство (10.6)

(10.8)

Так как система - линейно независима равенство (10.8) возможно только в случае, когда все коэффициенты линейной комбинации равны нулю

Учитывая, что , то из последних соотношений получаем , , что противоречит предположению о линейной зависимости, а значит, - опорный план ЗЛП (10.1).

Базис этого опорного плана получился, очевидно, из базиса исходного опорного плана путем введения в него вектора и удаления вектора . Таким образом, мы перешли от одного опорного плана к другому опорному плану . Этот переход был выполнен с помощью процедуры однократного замещения, т.е. из старого базиса был выведен вектор-столбец и введен .

Рис 10.3.

Ребро, соединяющее соседние угловые точки и . определяется угловой точкой и вводимым в базис вектором . Если бы вместо ввели бы другой вектор, то получили бы другое ребро, а, следовательно, и другую угловую точку (рис 10.3).

Замечание 1. Если не выполняются условия, наложенные на коэффициент разложения вектора по начальному базису, т.е. если , , то не удастся подобрать такое , чтобы одна из базисных координат обратилась в ноль. Значит, ребро не будет иметь другой вершины, т.е. оно является неограниченным лучом. Т.е. множество неограниченно.

Замечание 2. Если является вырожденным опорным планом, то может достигаться при нескольких , в этом случае, вектор, выводимый из базиса, определяется неоднозначно. Новый опорный план получится вырожденным и в зависимости от того, какой вектор выводится, будут получаться различные базисы одного и того вырожденного опорного плана , что приводит к образованию так называемого зацикливания алгоритма последовательного улучшения плана.

Процесс получения нового опорного плана заключается в выборе вектора, который подлежит введению в базис и определении вектора подлежащего исключению из базиса.

Критерий, используемый для определения вектора, подлежащего включению в базис, является основным элементом симплекс-метода.

Признак оптимальности опорного плана

Пусть дана задача:

(10.9)

(10.10)

(10.11)

Пусть известен некоторый опорный план, т.е. существует с базисом . Вычислим значения линейной формы и ограничений в точке

, (10.12)

Умножим равенство слева на и получим

(10.13)

Условие (10.10) можно записать

,

т.е.

Умножая последнее равенство слева на получим

(10.14)

Разложим вектор по базису и полученное выражение умножим слева на

Перепишем (10.14) с учетом (10.13)

.

(10.15)

Подсчитаем значение линейной формы в точке :

или

,

где

(10.16)

- оценки векторов относительно базиса .

Теорема 10.1. (необходимое условие оптимальности опорного плана). Для того, чтобы опорный план ЗЛП был оптимальным необходимо, чтобы оценки всех векторов условий относительно базиса этого опорного плана были неотрицательны ().

Д о к а з а т е л ь с т в о. Пусть - оптимальный опорный план с базисом . Выберем вектор , тогда

,

т.е. 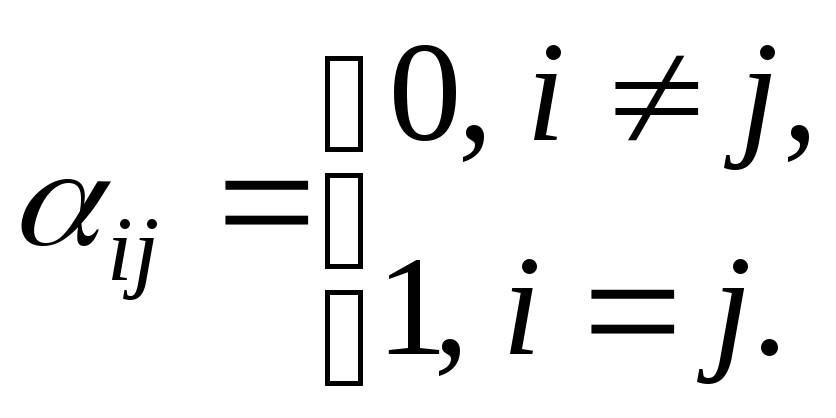. Оценка вектора относительно базиса

Таким образом, оценка базисного вектора относительно того же базиса равна нулю.

Теперь рассмотрим вектор () не принадлежащий базису . Допустим, что оценка вектора отрицательна. Перейдем к новому опорному плану так как было проделано выше при рассмотрении процедуры однократного замещения.

Вычислим значение линейной формы в точке :

С учетом того, что и

,

чего быть не может.

Следствие. Если не является оптимальным, то существует оценка , и тогда переход от этого неоптимального плана к новому опорному плану следует выполнять, вводя в базис вектор , так как в этом случае переход выполняется с увеличением значения линейной формы: .

Применение признака оптимальности опорного плана заключается, таким образом, в вычислении оценок всех небазисных векторов . Двум различным способам вычисления соответствует два вычислительных алгоритма симплекс - метода.

Первый способ состоит в вычислении коэффициентов разложения векторов по базису рассматриваемого опорного плана по формулам

и, затем, в вычислении оценок

Второй способ состоит в вычислении вектора-строки

и последующем вычислении оценок , .

В обоих способах приходится обращать матрицу , что весьма трудоемко. Вместе с тем, особенности перехода от одного опорного плана к соседнему позволяют получить простые рекуррентные формулы для пересчета параметров последовательных итераций .

Связь между параметрами последовательных итераций

Выведем формулы пересчёта коэффициентов разложения вектора по базисам двух соседних опорных планов.

Пусть известен опорный план с базисом .

Произведём операцию однократного замещения, а именно введем в базис вектор , и выведем из вектор , , т.е. мы предполагаем, что достигается на -ой позиции: