Относительность движения

Пусть имеется две системы отсчета. Одну из них мы будем считать неподвижной, а вторая пусть движется относительно неподвижной. Пусть имеется движущееся тело. Пусть нам известно, что за некоторое время Δt тело переместилось относительно движущейся системы отсчета на величину Δr₁, а подвижная система отсчета за то же время переместилась относительно неподвижной системы на величину Δr₂. Тогда суммарное перемещение тела относительно неподвижной системы отсчета, очевидно, будет равно: Δr = Δr₁ + Δr₂. Разделим это равенство на Δt и получим:

Где v₁ – скорость тела относительно подвижной системы отсчета, которую обычно называют относительной скоростью; v₂ – скорость подвижной системы отсчета относительно неподвижной, которую обычно называют переносной скоростью; v – скорость тела относительно неподвижной системы отсчета, которую обычно называют абсолютной скоростью. Таким образом, получаем классическую формулу сложения скоростей:

Эту формулу можно записать в другом виде, часто очень полезном при решении задач. Пусть имеется два движущихся тела. Известно, что скорость первого тела относительно неподвижной системы отсчета равна v₁, а скорость второго тела относительно неподвижной системы отсчета равна v₂. Чему равна скорость второго тела относительно первого? В этом случае следует связать с первым телом подвижную систему отсчета. Тогда скорость v₁ будет представлять собой скорость подвижной системы отсчета относительно неподвижной, то есть переносную скорость. Скорость v₂ будет представлять собой скорость тела относительно неподвижной системы отсчета, то есть абсолютную скорость. А скорость второго тела относительно первого (обозначим ее v₂₁) будет представлять собой скорость тела относительно подвижной системы отсчета, то есть относительную скорость. Запишем формулу сложения скоростей: 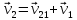. Откуда получаем:

Заметим, что скорость первого тела относительно второго равна: .

Динамика Первый закон Ньютона

В античной механике считалось, что для возникновения и поддержания движения тела на него надо действовать. Если на тело перестать действовать, то оно неизбежно остановится. Эта точка зрения как будто соответствовала повседневному жизненному опыту и поэтому продержалась очень долго. Только в конце XVI века Галилео Галилей изменил этот взгляд на природу движения. Он обратил внимание на то, что в реальных условиях на движущееся тело всегда действуют какие-либо силы сопротивления. Поэтому, если на движущееся тело перестать действовать, поддерживая его движение, то силы сопротивления продолжают действовать и под их действием тело в конечном итоге останавливается. Галилей мысленно попытался представить, как будет двигаться тело, если уменьшить или полностью исключить силы сопротивления. В результате мысленных экспериментов Галилей пришел к выводу, что если на движущееся тело вообще ничего не будет действовать, то оно будет двигаться вечно с постоянной скоростью. Предоставленное самому себе тело движется без изменения состояния своего движения. Наоборот, для того, чтобы изменить состояние движения тела требуется воздействовать на него со стороны. Этот факт получил название принципа инерционности Галилея.

Движение тела после прекращения действия на него других тел получило название движения по инерции. Из принципа инерционности следует, что для изменения состояния движения тела необходимо воздействовать не него со стороны. Значит, любое тело всегда сопротивляется попыткам изменить состояние своего движения, стараясь сохранить его неизменным. Это свойство тел называется инертностью.

Однако следует заметить, что любое движение описывается относительно какой-то системы отсчета. Системы отсчета бывают разные. Причем разные системы отсчета могут двигаться относительно друг друга произвольным образом. При этом может получиться следующая ситуация. Пусть имеется тело, на которое ничего не действует и оно движется по инерции без изменения состояния своего движения, то есть равномерно и прямолинейно относительно какой-либо системы отсчета. Однако, если имеется другая система отсчета, движущаяся относительно первой с ускорением, то относительно нее тело будет уже двигаться с ускорением, хотя на него ничего не действует. Получается, что относительно первой системы отсчета принцип инерционности Галилея выполняется, а относительно второй не выполняется.

Таким образом, принцип инерционности Галилея делит все системы отсчета на две категории. Хорошие системы отсчета, относительно которых принцип инерционности выполняется, и плохие, относительно которых он не выполняется. Исаак Ньютон обобщил результаты Галилея и сформулировал их в виде первого закона классической механики, который называется первым законом Ньютона: Существуют такие системы отсчета, относительно которых тело движется равномерно и прямолинейно или находится в состоянии покоя, если на него никакие другие тела не действуют или действие всех других тел полностью скомпенсировано.

Своим первым законом Ньютон утверждает, что хорошие системы отсчета существуют. Такие системы отсчета называются инерциальными. Дело в том, что принцип инерционности Галилея и остальные законы Ньютона, а значит и все законы классической механики справедливы только относительно инерциальных систем отсчета. Если существует хотя бы одна инерциальная система отсчета, то, значит, их существует множество. Ибо любая другая система отсчета, движущаяся относительно этой одной равномерно и прямолинейно тоже будет инерциальной. Это хорошо понимал Ньютон и указал абсолютно инерциальную систему отсчета, поместив начало системы координат в центр Солнца, а три координатные оси направив на три бесконечные звезды. Эта система сейчас конечно не является абсолютной, но она до сих пор является практически инерциальной почти для всех задач современного человечества. Очень хорошей инерциальной системой отсчета является система, связанная с поверхностью Земли. Хоть Земля и «крутится», но ускорение точек поверхности Земли настолько мало, что связанная с этим неинерциальность практически незаметна для большинства практических задач.