Движение по окружности

Рассмотрим движение тела по окружности. Если траекторией движения тела является конкретная окружность известного радиуса, то использовать для задания положения тела прямоугольную декартову систему координат совершенно необязательно. В этом случае легче поступить по-другому. Проведем через центр окружности прямую линию, задающую фиксированное направление. Пусть тело в данный момент времени находится в точке А на окружности. Если соединить точку А с центром окружности О радиусом, то угол φ между этим радиусом и фиксированным направлением полностью задает положение тела на окружности. В этом случае вместо двух координат x и y положение тела задается только одной величиной – углом φ.

Однако при таком способе задания положения тела должны измениться и некоторые другие кинематические характеристики движения. Так, например, скорость определяет быстроту изменения положения тела. При координатном способе задания положения скорость определяет быстроту изменения координаты тела. В нашем случае скорость должна определять быстроту изменения угла φ. Пусть за некоторый промежуток времени Δt положение тела на окружности изменилось так, что радиус, соединяющий его с центром окружности, повернулся на угол Δφ. Величина

называется угловой скоростью. Аналогично изменяется понятие ускорения. Пусть за промежуток времени Δt угловая скорость тела изменилась на Δω. Величина

называется угловым ускорением.

В системе СИ углы измеряются в радианах [рад]. Поэтому единицей измерения угловой скорости в системе СИ является [рад/с = 1/с = с^-1], а углового ускорения - [рад/с² = 1/с² = с^-2]. Один радиан – это угол, вырезающий на окружности длину дуги, равную радиусу окружности. Численно 1 рад = 180°/π ≈ 57,3°. Длина дуги, которую вырезает на окружности угол φ рад равна . Поэтому между угловыми и линейными характеристиками движения имеется простая связь: . Для центростремительного ускорения можно написать: .

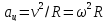Движение по окружности можно характеризовать еще такими величинами:

Период обращения Т – время одного полного оборота

Частота ν – количество оборотов, совершаемых за единицу времени

Для движения по окружности можно использовать уравнения равномерного и равноускоренного движения. Так если движение по окружности происходит с постоянной по величине скоростью, то можно говорить о равномерном движении по окружности и написать:

Если при движении по окружности угловая скорость линейно изменяется, то можно говорить о равноускоренном движении по окружности и написать:

Кинематика движения твердого тела

В этом разделе рассмотрим некоторые особенности кинематики движения твердого тела. Твердым телом называется система материальных точек (чаще всего бесконечная), расстояние между любыми двумя из которых в процессе движения остается постоянным. Пусть имеется движущееся твердое тело. Пусть в некоторый момент времени скорость некоторой точки А тела равна v_A, а скорость некоторой точки В равна v_B. Проведем прямую, соединяющую точки А и В. Пусть угол между вектором v_A и прямой АВ равен α, а между вектором v_B и этой прямой – β. Расстояние между точками А и В должно быть постоянным. Значит скорость с которой точка А удаляется от точки В должна быть равна скорости, с которой точка В приближается к точке А. То есть для любых двух точек А и В твердого тела должно выполняться условие: . Словами можно записать так: при движении твердого тела проекции скоростей любых двух точек тела на направление, соединяющее эти точки, должны быть одинаковыми.

Рассмотрим еще раз произвольно движущееся твердое тело. Пусть в некоторый момент времени скорость некоторой точки А тела равна v_A, а скорость некоторой точки В равна v_B. Проведем через точки А и В две прямые АО и ВО перпендикулярные векторам v_A и v_B до точки их пересечения О. Рассмотри две точки А и О. Проекции скоростей этих двух точек на направление АО должны быть одинаковыми. Но проекция вектора v_A на это направление равна нулю. Значит и проекция скорости точки О на направление АО тоже равна нулю. Рассмотри теперь пару точек В и О. Аналогичные рассуждения приводят к выводу о том, что проекция скорости точки О и на направление ВО тоже равна нулю. Это может быть только в одном случае: если скорость точки О равна нулю. Рассмотрим теперь произвольную третью точку С. Соединим ее с точкой О прямой СО. Так как скорость точки О равна нулю, то проекция ее скорости на направление СО равно нулю. А это значит, что проекция скорости точки С на направление СО тоже равна нулю, то есть скорость точки С направлена перпендикулярно СО. Причем это справедливо для любой точки тела. Получается, что в данный момент времени тело вращается вокруг неподвижной точки О. Таким образом, произвольное движение твердого тела в любой момент времени может быть представлено как чистое вращение вокруг некоторой неподвижной точки. Причем в следующий момент времени эта точка будет другой. Эта точка называется мгновенным центром вращения. Пусть точка О в данный момент времени является мгновенным центром вращения и тело вращается вокруг нее в угловой скоростью ω. Тогда для любой точки тела можно написать: