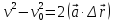Ускорение

Равномерное движение – самое простое, но практически не встречающееся в природе движение. Обычно при реальном движении скорости тел изменяются. Причем изменяются и по величине и по направлению. Аналогично понятию скорости, характеризующего быстроту изменения положения тела, можно ввести величину, характеризующую быстроту изменения скорости тела. Пусть за некоторый промежуток времени Δt скорость тела изменилась на Δv. Величина

называется средним ускорением. Ускорение – величина векторная.

Аналогично определению мгновенной скорости вводится понятие мгновенного ускорения:

Единицей измерения ускорения в системе СИ является [м/с²].

Проекции вектора среднего и мгновенного ускорения на оси координат:

;

Аналогично определяются проекции вектора ускорения на оси Y и Z.

Равноускоренное движение

Рассмотрим еще один простой вид поступательного движения – равноускоренного.

Равноускоренным называется движение с постоянным ускорением. Часто дается другое определение: равноускоренным называется движение, при котором за любые одинаковые промежутки времени скорость тела изменяется на одинаковую величину. Если под постоянством ускорения подразумевать его постоянство как по модулю так и по направлению, то эти два определения эквивалентны. В отличие от равномерного движения, равноускоренное движение не обязательно является прямолинейным.

Для равноускоренного движения понятия среднего и мгновенного ускорений совпадают. Значит ускорение, определяемое выражением 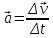, одновременно является и средним и мгновенным ускорением.

Пусть в начальный момент времени t₀ скорость тела была равна v₀, а в некоторый последующий момент t скорость тела стала равна v. Тогда можно написать: , а . Значит

или

Это выражение определяет зависимость скорости от времени для равноускоренного движения и является одним из основных уравнений. Если принять t₀ = 0, то . В проекции на ось Х эта зависимость записывается в виде:

(*)

Здесь v_0x – проекция вектора начальной скорости на ось Х; v_x(t) – проекция вектора скорости в момент времени t; а_х – проекция вектора ускорения на ось Х. Аналогично записываются зависимости скорости от времени в проекциях на оси Y и Z. Здесь принято t₀ = 0. Для того, чтобы записать еще одно основное соотношение для равноускоренного движения, воспользуемся так называемым графическим методом. Так как зависимость скорости от времени для равноускоренного движения является линейной, то график зависимости проекции скорости от времени представляет собой прямую линию. Нарисуем примерный график зависимости v_x от t. Как известно, на графике зависимости скорости от времени пройденное расстояние численно равно площади под графиком. Значит площадь заштрихованной трапеции на нашем графике равна изменению координаты:

Но . Значит, получается:

Обычно считают, что t₀ = 0 и записывают эту формулу в следующем виде:

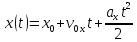
Эта формула представляет собой зависимость координаты х от времени для равноускоренного движения и является еще одной основной формулой. х₀ – начальная координата. Аналогично записываются зависимости координат y и z от времени. В векторном виде эта зависимость имеет такой вид:

Запишем еще одну формулу. Она не является основным соотношением для равноускоренного движения, но оказывается очень полезной при решении задач. Выразим время из (*): и подставим его в зависимость x(t). После преобразований получается формула:

Аналогичные зависимости можно записать в проекциях на другие оси координат. В общем виде эта зависимость записывается так: