Скорость

Скорость – это величина характеризующая быстроту изменения положения тела. Пусть за некоторый промежуток времени Δt тело переместилось из некоторого начального положения 1 в некоторое конечное положение 2. Если перемещение тела из положение 1 в положение 2 равно Δr, то величина

называется средней скоростью перемещения. В системе СИ единицей измерения перемещения является метр [м], а единицей измерения времени является секунда [с]. Поэтому единицей измерения скорости в системе СИ является [м/с]. Средняя скорость перемещения - векторная величина.

Если путь, пройденный телом при перемещении из начальной точки 1 в конечную точку 2 равен S, то величина

называется средней скоростью движения или средней путевой скоростью. Средняя скорость движения – величина скалярная.

Средняя скорость дает представление о том, как быстро изменилось положение тела за весь промежуток времени Δt, однако ничего не говорит о скорости движения тела в каждый момент времени внутри этого промежутка. Для более детального определения скорости имеется понятие о так называемой мгновенной скорости. Мгновенной скоростью называется средняя скорость перемещения, определяемая на очень маленьком, в пределе на бесконечно маленьком, промежутке времени. Математически это записывается следующим образом:

Мгновенная скорость – векторная величина.

Как и любой вектор, вектор скорости можно спроектировать на оси системы координат. Так проекции вектора средней скорости перемещения и мгновенной скорости на ось Х определяются так:

;

Аналогично определяются проекции скорости на оси Y и Z.

Равномерное движение

Перейдем теперь к рассмотрению конкретных простейших типов движения. Для начала рассмотрим простейшие типы поступательного движения. Самым простым типом поступательного движения является равномерное движение. Равномерным называется движение с постоянной скоростью. Часто дают другое определение: равномерным называется движение, при котором тело за любые равные промежутки времени совершает равные перемещения. Если учесть, что скорость – величина векторная и постоянство скорости подразумевает ее постоянство как по величине, так и по направлению, то понятно, что эти два определения полностью эквивалентны. Следует заметить, что равномерное движение всегда является прямолинейным.

Так как при равномерном движении скорость постоянна, то понятия мгновенной скорости и средней скорости перемещения полностью совпадают. То есть скорость, определяемая выражением , является также и мгновенной скоростью. Пусть в начальный момент времени t₀ положение тела определялось радиус-вектором r₀, а в некоторый последующий момент t радиус-вектор тела равен r. Тогда можно написать: , а . Значит

или

Эта формула определяет зависимость радиус вектора от времени для равномерного движения и является основной формулой. Часто начальный момент времени считают равным нулю (t₀ = 0) и записывают эту зависимость в виде: .

Эту зависимость можно записать в проекциях на оси координат:

,

,

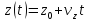
Здесь x₀, y₀, z₀ – начальные координаты тела в момент времени t₀ = 0; x, y, z – координаты тела в момент времени t; v_x, v_y, v_z – проекции вектора скорости на оси координат X, Y, Z.