Уравнение Бернулли

Рассмотрим узкую трубку тока и два ее сечения 1 и 2. Пусть площади сечений равны S₁ и S₂, а скорости потока в сечениях 1 и 2 равны v₁ и v₂. Рассмотрим очень маленький промежуток времени Δt. За это время жидкость в сечении 1 переместится на расстояние , а в сечении 2 на . Рассмотрим объем жидкости, заключенный между сечениями 1 и 2. Если давление жидкости в сечении 1 равно Р₁, а в сечении 2 – Р₂, то за время Δt силы давления совершают над выделенным объемом работу A (силы давления окружающей жидкости на боковую поверхность трубки тока направлены перпендикулярно поверхности трубка, а значит их работа равна нулю). Эта работа равна изменению энергии выделенного объема жидкости. Но за время Δt слой жидкости толщиной v₁Δt между штриховыми линиями в сечении 1 переместился в слой толщиной v₂Δt в сечении 2. Значит, совершенная силами давления работа равна разности энергий этих двух слоев жидкости:

Где массы слоев раны и , а h₁ и h₂ – высота сечений 1 и 2 относительно какого-либо нулевого уровня. Таким образом, получаем:

Сокращая на Δt и учитывая, что , получаем:

Это и есть уравнение Бернулли.

Величину 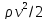можно назвать плотностью кинетической энергии, а величину - плотностью потенциальной энергии. Тогда можно написать: для стационарного течения идеальной жидкости сумма давления и плотностей кинетической и потенциальной энергий является постоянной для любого сечения потока жидкости.

Следствия из уравнения Бернулли

1) Пусть труба переменного сечения расположена горизонтально. Пусть по трубе течет жидкость. Рассмотрим два сечения трубы площадью S₁ и S₂ и запишем для них уравнение Бернулли:

Если S₁ < S₂, то v₁ > v₂ (уравнение неразрывности), а это означает, что P₁ < P₂. То есть, давление текущей жидкости в узких участках меньше, чем в широких.

2) Рассмотрим истечение жидкости из сосуда через узкое отверстие. Пусть имеется достаточно широкий цилиндрический сосуд, вблизи дна которого имеется узкое отверстие. Если сосуд заполнить жидкостью, то она будет вытекать из отверстия. При этом жидкость в сосуде и жидкость, вытекающую из отверстия можно рассматривать как единую трубку тока. Запишем уравнение Бернулли для двух сечений этой трубки. В качестве сечения 1 выберем верхний уровень жидкости в сосуде, а в качестве сечения 2 – выходное сечение отверстия. Так как площадь отверстия значительно меньше площади сосуда, то скорость жидкости в сечении 1 практически равна нулю. Кроме того, давления в сечениях 1 и 2 одинаковы и равны атмосферному давлению. Пусть высота верхнего уровня жидкости над отверстием равна h, а скорость вытекания жидкости из отверстия v. Тогда уравнение Бернулли имеет вид:

Отсюда получаем, что скорость вытекания жидкости из отверстия равна:

Эта формула называется формулой Торричелли.

3) Возникновение подъемной силы крыла самолета тоже является следствием уравнения Бернулли. При обтекании крыла самолета набегающим потоком воздуха на задней кромке крыла образуется завихрение, в котором воздух вращается против часовой стрелки (если крыло движется справа налево). По закону сохранения момента импульса должен возникнуть круговой поток по часовой стрелке. Такое движение воздуха возникает вокруг крыла. В результате скорость воздушного потока над крылом оказывается больше, чем под крылом. Но согласно уравнению Бернулли, там где скорость больше, давление меньше. Значит давление воздуха на нижнюю часть крыла самолета больше, чем на верхнюю. Эта разность давлений и создает подъемную силу.

Заметим еще, что на уравнении Бернулли основано действие многих технических устройств и, в частности, работа пульверизатора и карбюратора.