Гидростатика Давление. Закон Паскаля

Гидростатика – раздел механики, в котором рассматриваются жидкости и погруженные в них тела, находящиеся в состоянии равновесия. Мы в дальнейшем будем рассматривать так называемую идеальную жидкость. Идеальной жидкостью называется несжимаемая и невязкая жидкость.

Силы, с которыми отдельные части жидкости действуют друг на друга и на стенки сосуда, аналогичны силам упругости, возникающим в твердых телах. Если в сжатой жидкости мысленно выделить какой-либо объем, то на него со стороны окружающей жидкости будут действовать силы упругости, зависящие от степени сжатия жидкости. Соответственно жидкость в выделенном объеме действует на окружающую жидкость. Причем силы упругости, возникающие в жидкости и в газе, всегда обусловлены только деформацией сжатия. Поэтому сила, действующая со стороны жидкости на любую выделенную поверхность внутри жидкости (или газа), а также на поверхность твердого тела всегда направлена перпендикулярно (нормально) к поверхности. Сил упругости, направленных по касательной к поверхности внутри идеальной жидкости нет.

Упругие напряжения внутри жидкости называются давлением. Если на поверхность площадью S со стороны жидкости действует сила давления F, то давлением называется отношение силы к площади поверхности:

Давление – величина скалярная. Единицей измерения давления в системе СИ является паскаль - [Па] = [Н/м²].

Основным законом гидростатики является закон Паскаля: давление внутри неподвижной жидкости передается одинаково во всех направлениях. То есть сила давления, действующая на небольшую площадку, находящуюся внутри жидкости, не зависит от пространственной ориентации площадки. Причем давление может быть обусловлено как силой тяжести самой жидкости, так и внешними силами, действующими на жидкость (например, атмосферное давление).

Далее рассмотрим следствия из закона Паскаля.

Гидростатическое давление

Пусть однородная жидкость плотностью ρ находится в однородном поле тяжести. Выделим в жидкости тонкий вертикальный цилиндрический объем высотой h. На этот выделенный объем жидкости действуют: сила тяжести и силы давления со стороны окружающей жидкости. Силы давления окружающей жидкости на боковую поверхность цилиндра действуют со всех сторон одинаково и полностью друг друга компенсируют. Поэтому мы их далее рассматривать не будем. Остаются три силы: сила тяжести mg, сила давления на верхнее основание цилиндра F₁ и сила давления на нижнее основание цилиндра F₂. Так как выделенный объем жидкости находится в равновесии, то можно написать:

Если площадь сечения цилиндра равна S, то , , 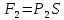. Где ρ – плотность жидкости, Р₁ и Р₂ – давление жидкости на верхнее и нижнее основания цилиндра. В результате получаем:

Полученная формула называется формулой для гидростатического давления. Гидростатическое давление создается самой жидкостью в результате действия на нее силы тяжести. Если имеется свободная поверхность жидкости, давление на которой равно Р₀ (чаще всего, атмосферное давление), то давление жидкости на глубине h равно:

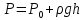
Рассмотрим теперь свободную поверхность неподвижной жидкости. Выделим тонкий плоский приповерхностный элемент жидкости. На этот элемент действуют: сила тяжести mg и сила давления со стороны нижележащей жидкости F. Так как выделенный элемент находится в покое, то эти две силы должны компенсировать друг друга. Но сила давления направлена перпендикулярно нижней поверхности элемента. Значит и сила тяжести должна быть направлена перпендикулярно поверхности жидкости. Получается, что свободная поверхность неподвижной жидкости располагается всегда перпендикулярно направлению действия силы тяжести.

Рассмотрим неподвижную жидкость и две точки внутри жидкости А и В, находящиеся на одном горизонтальном уровне. Выделим в жидкости узкий цилиндрический объем, ось которого совпадает с прямой АВ, а торцевые поверхности перпендикулярны АВ. В горизонтальном направлении на выделенный цилиндр действуют только силы давления на торцевые поверхности: P_AS и P_BS, где Р_А и Р_В – давление жидкости в точках А и В. Так как выделенный объем находится в равновесии, то эти силы должны друг друга уравновешивать. Значит давление в точках А и В должно быть одинаковым. Можно сделать вывод: давление в однородной жидкости во всех точках, находящихся на одном горизонтальном уровне, одинаково.

Одним из известных следствий данного положения является то, что верхние уровни однородной жидкости в сообщающихся сосудах находятся на одинаковой высоте.