Потенциальная энергия упругой деформации

Силы упругости, возникающие при упругой деформации, являются потенциальными.

Рассмотрим пружину жесткостью k. Один ее конец закрепим, а за другой конец будем ее растягивать. По закону Гука зависимость силы упругости от величины деформации пружины имеет вид: . Эта зависимость линейная. Графиком такой зависимости является прямая, проходящая через начало координат. На графике зависимости силы от перемещения совершенная работа численно равна площади под графиком. Значит при растяжении пружины на Δl Работа силы упругости численно равна площади заштрихованного треугольника: . Но работа силы упругости отрицательна, так как сила упругости всегда направлена в сторону противоположную направлению деформации: . Значит потенциальная энергия упругой деформации равна:

Заметим, что здесь мы приняли, что при недеформированном состоянии энергия пружины равна нулю. Чаще всего именно так и принимается. Хотя это необязательно и в некоторых случаях за ноль энергии упругой деформации бывает лучше принять энергию деформированной пружины.

Пусть пружина растянута на величину Δl₁. При дополнительном ее растяжении до величины Δl₂ сила упругости совершает работу:

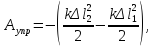
а работа внешней силы равна:

Закон сохранения энергии

Рассмотрим систему тел. На каждое тело системы действуют как внутренние так и внешние силы. Запишем изменение кинетической энергии для каждого тела системы:

Сложим все эти уравнения и получим:

Обозначим:

суммарные начальная и конечная кинетические энергии системы тел, а

суммарная работа всех внутренних и внешних сил, действующих на систему тел. Тогда можно написать:

Разложим внутренние силы системы на потенциальные и непотенциальные. Тогда работа всех внутренних сил равна сумме работ внутренних потенциальных и непотенциальных сил: . Но работа потенциальных сил равна изменению потенциальной энергии системы, взятой с обратным знаком:

Значит можно написать:

Сумма кинетической и потенциальной энергии называется полной механической энергией системы:

Окончательно можно написать:

Это и есть закон сохранения механической энергии. Читается так: изменение полной механической энергии системы тел равно сумме работ внешних сил и внутренних непотенциальных сил.

Если система тел замкнута и в ней не действуют внутренние непотенциальные силы, то полная мехеническая энергия системы должна оставаться постоянной. Тела системы могут взаимодействовать друг с другом, потенциальная и кинетическая энергия системы по отдельности могут изменяться, но их сумма в любой момент времени должна оставаться постоянной. То есть кинетическая энергия может переходить в потенциальную и наоборот при сохранении полной механической энергии.

Смысл закона сохранения энергии состоит в том, что энергия ниоткуда не берется и в никуда не исчезает. Она может только переходить из одних форм энергии в другие. Например, из кинетической в потенциальную, из механической во внутреннюю и так далее.

В механических системах тел самыми распространенными непотенциальными силами являются силы трения. Так как сила трения скольжения всегда направлена противоположно скорости, то ее работа всегда отрицательна. То есть, если в системе тел действуют силы трения, то работа внутренних непотенциальных сил всегда отрицательна. То есть внутренние непотенциальные силы чаще всего уменьшают механическую энергию системы. А куда же девается уменьшающаяся энергия? Все мы из опыта знаем, при трении тел всегда происходит их нагревание, то есть выделяется количество теплоты. Так вот результатом работы сил трения скольжения всегда является выделение теплоты. А сообщение системе теплоты приводит к увеличению ее внутренней энергии. Таким образом, наличие в системе тел сил трения приводит к тому, что часть механической энергии системы переходит во внутреннюю энергию, но при этом полная энергия системы остается постоянной. То есть можно написать: и закон сохранения энергии при наличии в системе тел сил трения можно записать так: