Центр масс

Рассмотрим движение системы двух тел. Запишем второй закон Ньютона для системы:

Заменим сумму внешних сил их равнодействующей: . Получаем:

Перепишем последнее уравнение в виде:

Обозначим:

Получается:

Полученное уравнение очень напоминает второй закон Ньютона для системы тел, так как М – это суммарная масса системы, F_p – равнодействующая всех внешних сил, действующих на систему, а а₀ – величина, имеющая размерность ускорения. Эту величину можно рассматривать как некое усредненное ускорение системы тел. Аналогично можно ввести величину, определяющую некую усредненную скорость системы:

и величину, определяющую положение системы тел в пространстве:

Все эти выражения можно написать для системы с произвольным количеством тел. Материальная точка, масса которой равна суммарной массе системы, а радиус-вектор определяется выражением:

называется центром масс системы тел и характеризует распределение масс в системе. Аналогично, скорость, определяемая выражением:

называется скоростью центра масс системы, а ускорение:

называется ускорением центра масс системы тел.

Таким образом, движение любой системы тел в целом можно описывать как движение материальной точки, называемой центром масс системы. Кроме того, можно сформулировать положение, которое называется теоремой о движении центра масс: центр масс системы тел движется так, как двигалась бы материальная точка, масса которой равна суммарной массе системы, под действием всех внешних сил, приложенных к системе. Если система тел замкнутая, то ее центр масс должен двигаться без ускорения, то есть равномерно и прямолинейно.

Реактивное движение

Всем известно так называемое явление отдачи. Если выстрелить из незакрепленной пушки, то пушка в результате отдачи после выстрела начнет двигаться в сторону противоположную скорости вылета снаряда. Если человек, стоя на гладком льду, оттолкнет от себя какой-либо тяжелый предмет, то сам начнет двигаться в противоположную сторону. Если надуть детский резиновый шарик и отпустить, то, выталкивая из себя воздух, сам шарик начнет быстро двигаться. На этом явлении отдачи основано реактивное движение.

В камере сгорания реактивного двигателя происходит сгорание топлива. Образовавшиеся при этом продукты сгорания (в основном газы) имеют очень большую температуру и с большой скоростью вылетают из сопла двигателя. При этом сам двигатель приобретает скорость отдачи. Если реактивный двигатель находится в космической ракете, то масса ракеты по мере сгорания топлива уменьшается. То есть сама ракета во время полета является телом переменной массы.

Рассмотрим ракету, летящую в космосе вдали от звезд и планет. Пусть продукты сгорания вылетают из сопла ракеты с постоянной скоростью u относительно ракеты. Пусть в некоторый момент времени масса ракеты равна М, а ее скорость относительно инерциальной системы отсчета, связанной со звездами, равна v. Спустя очень маленький промежуток времени Δt масса ракеты станет равна (Δm – масса топлива, сгоревшего за время Δt), скорость ракеты немного возрастет и станет равна , а сгоревшая масса топлива вылетит из сопла ракеты и будет иметь скорость . Так как система ракета – продукты сгорания изолированная, то должен выполняться закон сохранения импульса:

Раскрыв скобки и приведя подобные, получаем:

Так как Δt очень малая величина, то и Δm тоже очень малая величина. Значит последнее слагаемое в последнем уравнении является произведением двух очень малых величин (бесконечно малая второго порядка). Поэтому этим слагаемым можно пренебречь. Пусть 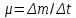- секундный расход топлива – масса топлива, сгорающая в единицу времени. Окончательно имеем:

Это уравнение называется уравнением Мещерского. Величина называется реактивной силой. Она обусловлена отдачей при истечении продуктов сгорания из сопла реактивного двигателя. Она приложена к ракете и не зависит от устройства двигателя, а определяется только секундным расходом топлива и скоростью истечения газов из сопла. Направлена реактивная сила противоположно направлению скорости истечения газов.

Принцип реактивного движения заключается в том, что при истечении из сопла газы приобретают импульс. Согласно закону сохранения импульса ракета приобретает в противоположном направлении равный по модулю импульс.