6 Перетин прямої та площини

6.1 Визначити точку перетину прямої з площиною. Визначити видимість елементів.

Рекомендації до розв’язання задачі 6.1:

а) необхідно визначити яке положення займає площина Δ. Фронтальна проекція точки перетину вже відома за збиральною властивістю проекціюючої площини. Горизонтальну проекцію добудувати за властивістю приналежності точки прямій.

б) та в) Для побудови точки перетину використовується загальний алгоритм:

- пряма заключається у проекціюючу площину (слід, що має збиральну властивість збігається з відповідною проекцією прямої);

- будується лінія перетину заданої площини з проекціюючою (одна з проекцій лінії перетину збігається із слідом площини, а інша будується за властивістю приналежності прямої площині);

- точка перетину знаходиться на перетині заданої прямої та лінії перетину площин;

- видимість визначається за методом конкуруючих точок.

6.2 Побудуйте лінію перетину двох 6.3 Через точку А провести пряму,

площин. яка перетинає пряму n під прямим

к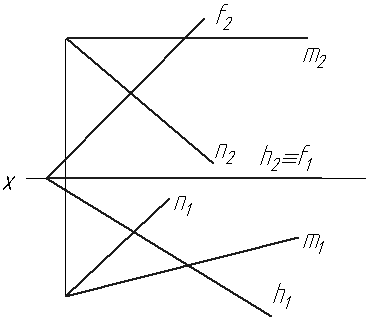утом.

Рекомендації до розв’язання задачі 6.2:

Для побудови лінії перетину доцільно побудувати точки перетину прямих m та n з площиною (f ∩ h), а потім, через дві отримані точки провести лінію перетину заданих площин.

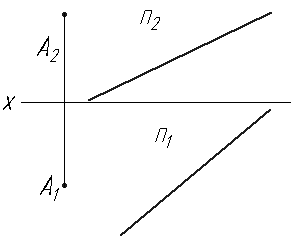
Рекомендації до розв’язання задачі 6.3:

1) через точку А потрібно провести площину перпендикулярну до прямої n. Задати цю площину фронталлю та горизонталлю (пряма n буде перпендикуляром до цієї площини);

2) знайти точку перетину прямої n з побудованою площиною;

3) через точку А та отриману точку провести пряму, яка і буде шуканою прямою.

7 Переріз поверхні площиною

7.1 Побудувати лінію перерізу 7.2 Побудувати лінію перерізу

нахиленої піраміди заданою нахиленого конуса заданою

площиною площиною

7.3 Добудувати горизонтальну та профільну проекції кулі з вирізом, виконаним проекціюючими площинами.

7.4 Побудуйте лінію перетину циліндра площиною загального положення.

7.5 Побудуйте лінію перетину призми площиною  (f х h).

8 Перетин поверхонь з прямою

8.1 Знайти точки перетину прямої з поверхнею заданого тіла. Визначити видимість. в

9 Способи перетворення проекцій

9.1 Перетворити пряму загального 9.2 Побудувати точки перетину

положення у пряму горизонтального сфери з прямою.

рівня за допомогою методу заміни

площин проекцій.

9.3 Визначити положення центру 9.4 Методом плоско-паралельного

кола, описаного навколо трикутника. переміщення перетворити пряму

Використати метод обертання навколо загального положення на

проекціюючої осі. горизонтально-проекціюючу.

9.5 Визначити положення центру кола, описаного навколо трикутника. Використати метод обертання навколо прямої рівня.