- •1. Установившееся неравномерное плавноизменяющееся движение жидкостей в открытых руслах.(осн-ые понятия и опред-ия).
- •2. Основное диф. Ур-ие установившегося неравномерного режима (1-ый и 2-ой вид).
- •4. Четыре вспомагательных понятия: удельная энергия сечения, критическая глубина, нормальная глубина, критический уклон и критическое состояние потока.
- •5. Исследование форм свободной пов-ти потока. Интегрирование основного диф ур-ия.
- •6. Построение кривой свободной поверхности.
- •7. Гидравлический прижок. Основные сведения.
- •8. Основное уравнение гидравлического прыжка (вывод)
- •9. Формула сопряженных глнбин для прямоугольных русел. Потеря энергии в прыжке. Длина прыжка и послепрыжкового участка.
- •10. Отогнанный, надвинутый прыжки и прыжок в критическом состоянии.
- •11. Классификация водосливов.
- •12. Основная ф-ла расходов водосливов. Коэф расхода
- •13.Водослив с тонкой стенкой, типы струй, условия подтопления, учет бокового сжатия
- •14. Использование водосливов с тонкой стенкой для измерения расхода
- •16. Определение глубины на пороге водослива. Учет бокового сжатия.
- •17. Водослив практического профиля. Безвакуумные и вакуумные водосливы. Пропускная способность водосливов.
- •19.Определение глубины в сжатом сечении.
- •20. Общие понятия и терминология сопряжения бьефов при устройстве плотины.
- •21.Глубина в сжатом сечение и глубина ей сопряженная. Формы сопряжения бьефов.
- •22.Сопряжение свободной струи с потоком в нижнем бьефе. Дальность полёта струи.
- •24.Гидравлический расчёт водобойных колодцев, водобойных стенок.
- •25.Основные понятия, классификация сопрягающих сооружений.
- •26 Расчет одноступенчатого перепада
- •27. Многоступенчатые перепады, расчет многоступенчатых перепадов
- •28. Расчет быстротока по допустимой скорости.
- •29. Основные сведения о волнах. Классификация волн.
- •30. Классификация водоемов и прибрежных зон.
- •Определение высоты hв и длины волны λ .
- •33. Коэффициент фильтрации и методы его определения. Равномерное и неравномерное движение грунтовых вод.
- •34. Диф. Уравнение неравномерного движения грунтовых вод. Формы кривых депрессий.
- •35. Интегрирование ду для случая плоской задачи.
- •37. Галерея расположенная выше водупора.Висячая галерея.
- •41.Резкоизменяющееся движение грунтовой воды.Общие указания.
- •42.Основные дифуравнения установившегося движения грунтовой воды.
- •43.Напорная функция.Потенциал скорости.Линии равного потенциала.
- •44.Уравнение Лапласа.Линии тока.Функция тока.Гидродинамическая сетка.
- •45.Гидродинамическая сетка в случае гидротехнического сооружения.
- •46. Основы гидравлического моделирования. Общие указания.
- •47. Понятия о подобии гидравлических явлений.
- •48. Критерии динамического подобия (случай, когда на жидкость действует только сила тяжести).
- •49. Критерий динамического подобия (случай, когда на жидкость действуют только силы трения).
- •50. Основные указания о моделировании гидравлических явлений.
4. Четыре вспомагательных понятия: удельная энергия сечения, критическая глубина, нормальная глубина, критический уклон и критическое состояние потока.
Удельная энергия сечения Э- частное значение полной удельной энергии, подсчитанное в предположении, что плоскость сравнения проведена через самую нижнюю точку сечения русла.
 (1) или
(1) или
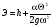
Для
прямоугольного русла:
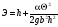 ,
где b- ширина русла. Заменив
расход Q через удельный
получим
,
где b- ширина русла. Заменив
расход Q через удельный
получим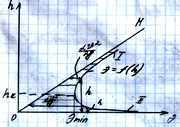
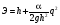
Проведем
анализ ф-лы (1): Считаем, что при заданном
Q, вода в данном сечении
может протекать при различных h
(в зависимости от i и m)
т.е. значение Э будет разное Э=f
(h). Из ур-ия (1) видно, что:
а) при
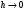 ,
получаем
,
получаем
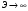 (т.к.
при
(т.к.
при
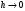 второе слагаемое правой части ур-ия
стремится к бесконечности); б) при
второе слагаемое правой части ур-ия
стремится к бесконечности); б) при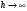 получаем Э так же стремящееся к
бесконечности. Известно, что если
непрерывная ф-ция при граничных знач-х
независимых переменных оказ-ся = +
получаем Э так же стремящееся к
бесконечности. Известно, что если
непрерывная ф-ция при граничных знач-х
независимых переменных оказ-ся = + ,
то в промежутке данная ф-ция имеет по
крайней мере 1-н минимум.
,
то в промежутке данная ф-ция имеет по
крайней мере 1-н минимум.
Подробный анализ показывает, что Э=f(h) может быть представлена кривой.
Кривая Э явл-ся ф-ей от h имеет 2 асимптоты: ОМ направлена под углом 45; ОЭ-ось координат. Штриховкой показано изменение скоростного напора.
Критическая
глубина-глубина, отвечающая минимуму
удельной энергии сечения. Если задано
поперечное сечение русла, а также расход
Q, то hк
определится из ур-ия
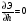
Для прямоугольного сечения имеем
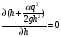 Откуда имеем
Откуда имеем
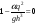 .
Из этого ур-ия определим hк,
где h=hк
.
Из этого ур-ия определим hк,
где h=hк
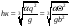 Для треугольного русла:
Для треугольного русла:
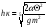 Для трапецеидального русла. Здесь
выражение для hк в явном
виде получить не удается ( можно найти
только путем подбора). Практически
определяют по особому графику.
Для трапецеидального русла. Здесь
выражение для hк в явном
виде получить не удается ( можно найти
только путем подбора). Практически
определяют по особому графику.
Круглоцилиндрические русла. Для этих русел величину hк можно найти, пользуясь спец-ым графиком.
Нормальная глубина-глубина, которая при заданном расходе установилась бы в русле, если бы в этом русле движение было равномерным. Нормальная глубина обозначается через h0.
Критический уклон- такой вооброжаемый уклон, который надо придать рассматриваемому цилиндрическому руслу, чтобы при заданном расходе Q и равномерном движении воды в русле, нормальная глубина h0 оказалась равной критической hк ( h0=hк)
Очевидно,
а) если iк> i,
то hк<h0;
б) если iк< i,
то hк> h0;
в) если iк = i,
то hк=h0.
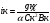
Различают 3 состояния безнапорного потока:
- спокойное, если h>hк;
-бурное, если h<hк;
-критическое состояние потока, если h=hк. В случае критического состояния потока всегда должно быть равномерное движение, характеризуемое условием i=iк.
5. Исследование форм свободной пов-ти потока. Интегрирование основного диф ур-ия.
Русло с прямым
уклоном (i>0). Рассматривая
неравномерное движ-ие в русле с прямым
уклоном различаем 3 случая: 1-ый,
характеризуемый условиями h0>hк
и i<iк ,
здесь получим три возможные формы
свободной пов-ти: три кривые подпора; 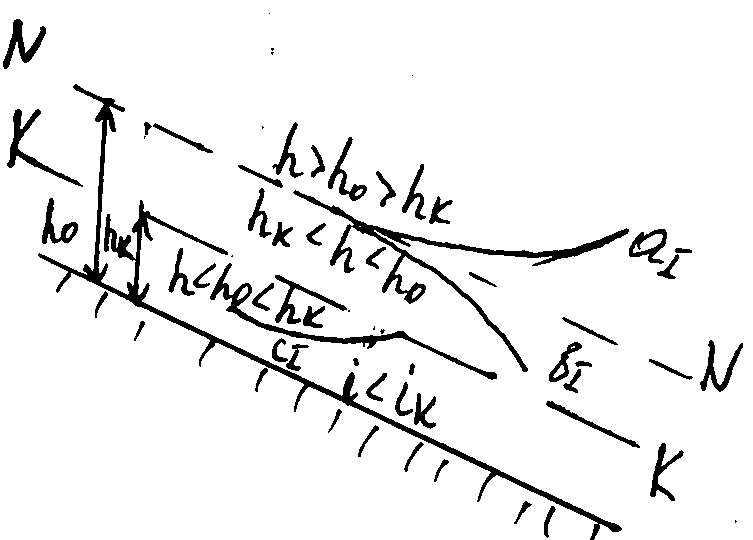
2-й,
характеризуемый условиями h0<hк
и i>iк.
Здесь также получим три возможные формы
свободной пов-ти: три кривые подпора;
3-й,
характеризуемый условиями h0=hк
и i=iк, здесь
получим только 2 возможные формы свободной
пов-ти: кривые спада. Заметим, что кривая
подпора- такая кривая свободной пов-ти,
вдоль которой( по течению) глубины потока
возрастают; кривая спада-кривая свободной
пов-ти, вдоль которой глубины потока
уменьшаются.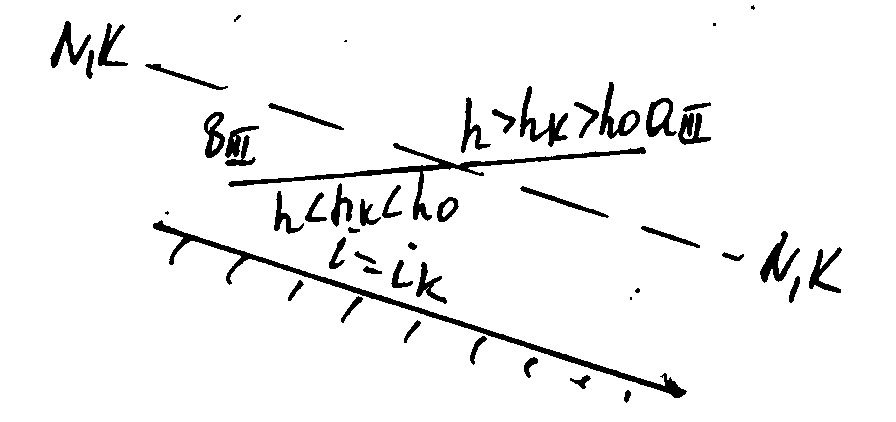
Русло с горизонтальным дном (i=0). В этом случае может быть одна из двух свободных пов-тей: кривая спада или кривая подпора.
Русло с обратным уклоном дна (i<0). Здесь, как и в случае i=0 , получаем только 2 свободные пов-ти: кривая спада и кривая подпора.
ДУ неравномерного движ-ия воды необходимо привести к виду удобному для интегрирования.
 -
для цилиндрического русла.
-
для цилиндрического русла.
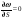 ,
,
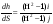 ,
где
,
где
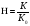 -
относительный модуль расхода.
-
относительный модуль расхода.
Дальнейшее
решение этого ур-ия было предложено
учеными-исследователями Брессо, Чугаев,
Бахметьев, Агроскин, Павловский, Рахманов
и др. Рассматривая интегрирование ДУ
Бахметьев предложил заменить
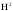 величиной
величиной
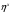 ,
,
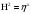 ,
где
,
где
 -относительная
глубина .
-относительная
глубина .
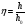 ,
h-глубина в данном сечении,
,
h-глубина в данном сечении,
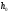 -глубина
при равномерном движ-ии , x-
гидравлический показатель русла,
зависящий от параметров канала, т. е.
глубины, ширины канала. Опр-ся по спец-ым
ф-ам
-глубина
при равномерном движ-ии , x-
гидравлический показатель русла,
зависящий от параметров канала, т. е.
глубины, ширины канала. Опр-ся по спец-ым
ф-ам
 .
Проинтегрировав это выр-ие на отрезке
длины, получим ур-ие
.
Проинтегрировав это выр-ие на отрезке
длины, получим ур-ие
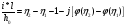
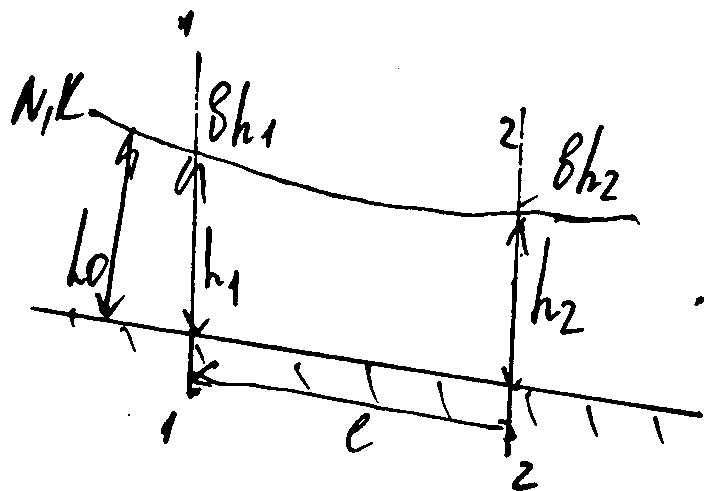
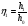 ,
,
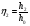
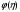 -ф-ция,
зависящая от относит-ой глубины и
определ-ся по спец-ым табл-ам и зависит
от гидравлического показателя x;
j- параметр кинематичности.
-ф-ция,
зависящая от относит-ой глубины и
определ-ся по спец-ым табл-ам и зависит
от гидравлического показателя x;
j- параметр кинематичности.
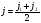 ,
,