33. Коэффициент фильтрации и методы его определения. Равномерное и неравномерное движение грунтовых вод.
Коэффициент фильтрации имеет размерность
скорости, и при I=1 предст-ет
собой скорость фильтрации. Зная фиктивную
скорость, мы можем опр-ть расход фильтрац.
потока:
;
Для опред-я коэф-та фильтрации существует 3 метода:
-
Лабораторный метод: Кф опред-ся в спец. приборах, в которые закладываются образцы грунта.
-
Расчётный метод: Кф опред-т расчётом по эмпирич. формулам.
-
Полевой метод: Кф опр-т в поле путём откачки воды из спец-но устроенного колодца (шурфа).
=0,1-0,01см/с
100-10
м/сут(песка)
=0,00001-0,000001
см/с
0,01-0,001
м/сут(глины)
При равномерном дв-ии Е-Е совпадает с Р-Р и картина дв-я грунтовых вод имеет след. вид:
-гидравлический
уклон, I-пьезометрический
уклон, i – геодезический
уклон.
Для плоской задачи
-при равном. режиме движения.
- это основное ур-е безнапорного устан-гося
дв-я грунтовых вод в случае плоской
задачи.
При неравномерном плавноизмен. дв-ии грунт. вод картина имеет вид:
Изучение плавноизмен. безнапорного
дв-я грунт. вод основано на 2-х допущениях: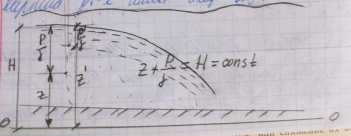
а) Живые сечения считаются плоскими, т.к. кривизна невелика.
б) живые сечения считаются верт-ми, т.к. i мало.
Учитывая сказанное, расчётная модель
имеет вид:
Пьезом. уклон для данной пов-ти можно записать в виде:
Подставив это значение в ф-лу Дарси, получим:
Приняв, что средняя скорость по сечению=υ , т.е. U=υ можно записать:
- формула Дюпии.
- уклон кривой депрессии в точке,
принадлежащей данному живому сечению.
34. Диф. Уравнение неравномерного движения грунтовых вод. Формы кривых депрессий.
При движении грунтовой воды в цилиндрич. русле пьезом. линия совпадает со свободной пов-тью. Уклон своб. пов-ти потока I может быть представлен 2-мя различными зависимостями.
Рассм. след. схему:
В этих формулах i – уклон
дна водоупора. Учитывая эти соотношения
ф-лу Дюпии можно переписать в виде:
где h – глубина в рассм-м сечении, υ – ср. скорость в этом сечении.
Если кривая своб. пов-ти имеет подъём, то ф-ла примет вид:
Зная ср. скорость υ можно опр-ть расход грунтового потока:
- это ДУ, относящееся к общему случаю цилиндрич. русла с прямым уклоном дна. Для случая плоской задачи ур-е примет вид:
Если i=0, то
Формы своб. пов-ти (Кривые депрессии).
В случае дв-я грунт. вод всегда имеем i<iкр, т.е. в этом случае hкр=0 , т.е. зона с
отсутствует.
Случаи:
а. i>0
б. i=0 (неравномерный режим)
в. i<0
35. Интегрирование ду для случая плоской задачи.
Рассм-м след. схему:
Анализируя данную схему и интегрируя
уравнение
окончательно получим:
или
Если необходимо определить глубину воды в любой точке своб. пов-ти, то примен-ся ф-ла:
где х - это расстояние от начала кривой своб. пов-ти до места, где опред-ся h.
36.Приток воды к галерее расположенной на водоупоре.
Где h1-глубина грунтовой воды в естественном состоянии,
h2-глубина воды в галерее,
k- коэффициент фильтр-и,
L-длина влияния галереи устоновленного наосновании результата
Изыскания.
Т.о на 1м длины галереи с двух её сторон будет поступать расход равный 2q.