Д

Принцип соответствия

ля решения подобных вопросов в 1918 году Бор использовал принцип соответствия, который первоначально иногда называли принципом аналогии. Несмотря на неприменимость классической физики к внутриатомным процессам, она вполне корректно объясняет физические явления в макроскопической области, а также, в ряде случаев, и в микроскопической: движение заряженных частиц в электрическом и магнитном полях, тепловое движение атомов и молекул в газе и др. Поэтому можно считать установленным, что классическая теория «макроскопически корректна», т.е. она правильно описывает физические явления в том предельном случае, когда квантовые скачки пренебрежимо малы. В этих случаях предсказания квантовой и классической теорий должны совпадать.

Сначала Бор сформулировал принцип соответствия для простейшего случая атома водорода. Пусть электрон находится на стационарной орбите с главным квантовым числом n. Движение электрона по орбите в теории Бора-Зоммерфельда описывается классической физикой. С ее точки зрения электрон совершает периодическое движение по орбите радиусом , обладая при этом моментом импульса . Комбинируя эти две формулы, можно вычислить частоту обращения электрона:

. (17.18)

Согласно классической электродинамике, частота испускаемого электромагнитного излучения должна равняться  и ее обертонам: 2, 3, и т.д. При этом интенсивность излучения на различных частотах определяется коэффициентами разложения движения электрона в ряд Фурье:

.

С точки зрения теории Бора-Зоммерфельда электрон излучает при переходе с n-ой орбиты на другую, характеризующуюся меньшим значением квантового числа . Частота излучения при этом составляет

.

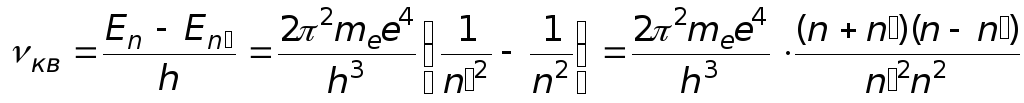В случае больших значений n и , если разность мала, то

. (17.19)

Таким образом, при 1, 2, 3 и т.д. частоты излучения совпадают с обертонами классической частоты (17.18).

Бор предположил, что вероятности переходов электрона с n-ой орбиты на нижележащие, как и в классической теории, определяются коэффициентами при классических гармониках, что позволяет сделать вывод об интенсивности излучения на различных частотах. Более того, Бор считал, что и в случае малых значений главного квантового числа n, когда частоту даже приближенно нельзя считать равной какой-либо из классических частот, все-таки можно установить соответствие между конкретными значениями классических и квантовых частот таким образом, чтобы коэффициенты определяли вероятности соответствующих квантовых переходов, а значит, и интенсивности соответствующих спектральных линий. Бор не пытался объяснить существование такого соответствия между классическим и квантовым описанием. Принцип соответствия следовало принять как факт, так же, как и основные постулаты Бора. Использование принципа соответствия позволило, в частности, установить правило отбора для квантовых чисел и m. Оказалось, что k при квантовых переходах может изменяться лишь на 1, а для магнитного квантового числа m существует правило m  0, 1, поэтому не все спектральные линии, ожидаемые согласно вычислениям Зоммерфельда, имеют место в действительности в случае нормального эффекта Зеемана.

Опираясь на периодическую систему Менделеева и идею Дж. Дж. Томсона о том, что электроны в атоме делятся на группы, располагающиеся отдельными слоями, Бор и другие ученые развили полуэмпирическую теорию строения многоэлектронных атомов. К этому времени уже было известно, что заряд ядра равен Ze, где Z – порядковый номер элемента в таблице Менделеева. Электронейтральность атома в целом означала, что число электронов в атоме равно Z. По Бору, атом водорода содержит один электрон с квантовыми числами n = 1 и k = 1. Исходя из соображений о свойствах гелия, Бор предположил, что оба электрона в атоме гелия характеризуются теми же значениями квантовых чисел, что и в атоме водорода. Следующие восемь элементов с лития по неон, согласно Бору, образуются при последовательном заполнении электронами L-оболочки, характеризующейся значением главного квантового числа n = 2; при этом для лития и бериллия k = 1, а для остальных элементов с бора по неон k = 2.

В 1920 году Зоммерфельд, изучая мультиплетный характер спектров щелочных металлов, ввел для характеристики состояний атома в целом новое квантовое число j. Оно определяло момент импульса всего атома. Кроме того, вместо азимутального числа было введено орбитальное квантовое число l = k – 1 и установлено, что l и j для атома с одним валентным электроном связаны соотношением . При этом в случае l = 0 полный момент импульса атома оказывался отличным от нуля, так как квантовое число j получалось равным ½.