К

Опыты Франка и Герца

вантовые постулаты Бора нашли непосредственное экспериментальное подтверждение в опытах Джеймса Франка и Густава Герца, результаты которых были опубликованы в 1914 году. Целью этих опытов было определение ионизационных потенциалов различных атомов. Для этого Франк и Герц использовали следующую установку. Нить накала выполняла роль катода, на который подавался отрицательный потенциал относительно пластины – анода. Анодный ток измерялся гальванометром. Непосредственно перед анодом помещалась сетка, на которую подавался небольшой (порядка 0,5 В) положительный потенциал относительно анода. Опыт производился в парах ртути и состоял в измерении анодного тока в зависимости от ускоряющего потенциала. Действие установки было описано Франком и Герцем следующим образом: «Пока ускоряющая разность потенциалов меньше, чем замедляющая, ток [на анод] равен нулю. Как только ускоряющая разность потенциалов превысит замедляющую, через коллектор (анод) начнет течь ток, который будет увеличиваться до тех пор, пока ускоряющая разность потенциалов не станет равной ионизационному потенциалу». То есть Франк и Герц предполагали, что пока кинетическая энергия электронов меньше энергии ионизации атомов ртути, столкновения между электронами и атомами будут упругими. При упругих столкновениях электроны теряют незначительную часть своей энергии и способны преодолеть задерживающую разность потенциалов между сеткой и анодом. Если же ускоряющая разность потенциалов V станет больше ионизационного потенциала, то столкновения электронов с атомами станут неупругими. Электроны будут ионизировать атомы, теряя почти всю свою энергию, и поэтому не будут способны дойти до анода. «Таким образом, – писали Франк и Герц, – как только ускоряющая разность потенциалов станет больше потенциала ионизации, ток гальванометра упадет до нуля». При этом они предположили, что дальнейшее увеличение ускоряющей разности потенциалов снова будет обусловливать рост анодного тока до тех пор, пока величина eV не станет равной удвоенному значению энергии ионизации, когда ток должен снова резко уменьшиться, и т.д.

Рис. 41. Кривая зависимости анодного тока от ускоряющей разности потенциалов в опытах Франка и Герца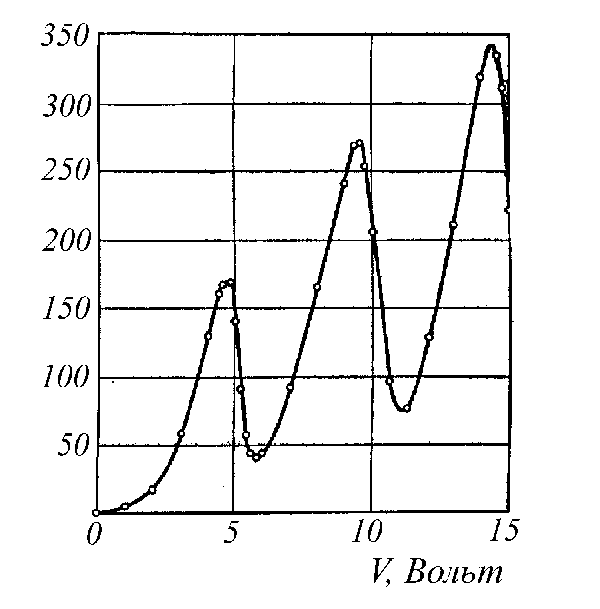

Именно такие вольтамперные характеристики и были получены: они представляли собой ряд острых максимумов, отстоящих друг от друга на 4,9 В (рис. 41). Однако была ли эта величина ионизационным потенциалом ртути? Франк и Герц проверили, не наблюдается ли в их опыте излучение атомами ртути, и установили, что атомы ртути не излучают, пока разность потенциалов между катодом и сеткой остается ниже 4,9 В. Когда же разность потенциалов превышала эту величину, атомы ртути испускали единственную линию при 253,6 нм, хотя спектр ртути содержит много линий, длины волн которых соответствуют значениям разности потенциалов, меньшим 4,9 В.

Истинный смысл результатов, полученных Франком и Герцем, был осознан позже, когда теория Бора приобрела известность. Стало очевидным, что при неупругих соударениях с электронами атомы ртути переходят из основного () в первое возбужденное состояние (). Но во время проведения этих экспериментов даже Нильс Бор, выдвинувший идею дискретности энергетических состояний электрона в атоме в качестве одного из постулатов своей теории, не сознавал, что результаты этих опытов подтверждают его радикальное предположение.

В 1925 году Франку и Герцу за эту работу была присуждена Нобелевская премия.

Д

Развитие квантовой теории атома

альнейшее развитие теории Бора происходило в направлении поисков более общих условий, определяющих стационарные состояния атомов. Сначала Бор принял орбиты электрона круговыми. Однако, согласно классической теории, электрон, движущийся в кулоновском поле ядра, описывает эллиптическую орбиту. При этом условия квантования Бора (17.2) оказывалось недостаточно, чтобы из числа всех механически возможных эллипсов выбрать отвечающие стационарным состояниям атома.

В 1915 году независимо друг от друга Арнольд Зоммерфельд и Уильям Вильсон ввели более общие условия квантования, обобщенные впоследствии Карлом Шварцшильдом и Паулем Эпштейном. Условия эти были сформулированы для систем со многими степенями свободы, совершающих многократно периодическое движение, когда обобщенные координаты периодически изменяются между крайними значениями и .

Постулат квантования электронных орбит, введенный Зоммерфельдом, являлся обобщением постулата Планка о квантовании энергии линейного осциллятора E = nh. Последнее соотношение можно переписать в виде

. (17.7)

Полная энергия осциллятора E определяется выражением

. (17.8)

Разделим обе части (17.8) на E

, (17.9)

и введем обозначения:

, . (17.10)

Тогда соотношение (17.9) записывается в виде

. (17.11)

Это есть не что иное как уравнение эллипса. Таким образом, фазовая траектория линейного осциллятора представляет собой эллипс. Вычисления площади эллипса S = ab с использованием выражений (17.10) приводят к величине . С другой стороны площадь эллипса, служащего фазовой траекторией линейного осциллятора, равна . Принимая во внимание (17.7), можно переписать планковское условие квантования энергии линейного осциллятора в виде:

. (17.12)

Итак, условие квантования (17.12), рассматриваемое как общее требование, заключается в том, что в атомных системах величина , имеющая размерность действия, должна быть кратной постоянной Планка h. Согласно Зоммерфельду, если механическая система с несколькими степенями свободы описывается с помощью обобщенных координат и соответствующих им обобщенных импульсов (T – кинетическая энергия системы), то стационарными являются лишь те состояния системы, которые удовлетворяют условиям квантования

, (17.13)

где h – постоянная Планка, – квантовое число, имеющее целочисленное значение.

Плоская эллиптическая орбита электрона в атоме представляет собой движение с двумя степенями свободы, которым отвечают полярные координаты r и . Поэтому, согласно условиям квантования (17.13), стационарными будут те эллипсы, для которых справедливы равенства

; . (17.14)

Целые числа и получили названия радиального и азимутального квантовых чисел. Расчеты показали, что энергия E и момент импульса электрона для стационарных орбит определяются выражениями

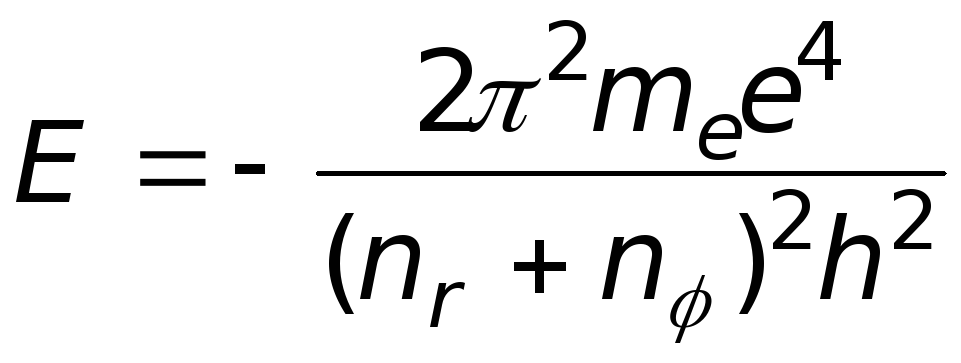; . (17.15)

Сумма радиального и азимутального квантовых чисел получила название главного квантового числа. Именно главное квантовое число определяло значение энергии электрона на стационарной орбите.

Предложенные Зоммерфельдом условия квантования приобрели новый смысл в свете созданной в 1916 году Эренфестом теории адиабатических инвариантов. Адиабатическими инвариантами называются величины, которые практически остаются постоянными в незамкнутой системе в случае чрезвычайно медленного (адиабатического) изменения ее внутренних или внешних параметров. Общее выражение для адиабатического инварианта имеет вид , где q – некоторая обобщенная координата, p – соответствующий ей обобщенный импульс.

Таким образом, условия квантования Зоммерфельда обнаружили свой глубинный смысл. При адиабатическом изменении внутренних или внешних параметров микроскопической системы квантующиеся величины должны оставаться постоянными, т.е. должны являться адиабатическими инвариантами. Поэтому после получения чисто классических решений для некоторой микроскопической системы следовало наложить условия квантования на те физические величины, которые являются адиабатическими инвариантами. Теория адиабатических инвариантов давала критерий квантующихся величин и вплоть до создания квантовой механики была единственной руководящей идеологией применения правил квантования.