3.2. Характеристики варіації ознаки у варіаційних рядах

Характеристиками варіації ознаки у варіаційних рядах є розмах варіації, дисперсія, середнє квадратичне відхилення, середнє лінійне відхилення, квадратичний коефіцієнт варіації, лінійний коефіцієнт варіації, коефіцієнт осциляції. Останні три характеристики є відносними величинами і можуть виражатись відношенням або у відсотках. Означення і спосіб знаходження характеристик залежить від типу варіаційного ряду: з. в. р., д. в. р. чи і. в. р.

Кожна із числових характеристик варіації може розглядатись як статистичний аналог і точкова оцінки відповідної числової характеристики генеральної сукупності, з якої вибрана статистична сукупність, що згрупована у даний варіаційний ряд.

Розмахом варіації з. в. р. і д. в. р. називається різниця між найбільшим і найменшим значеннями варіант відповідно у_і (і=) та х_k (k=):

R_у = y_n – y₁; R_х = x_m – x₁.

Розмахом варіації і. в. р. називається різниця між правою межею останнього (т-го) і лівою межею першого інтервалів:

.

Дисперсією з. в. р. і д. в. р. називається середня квадратів відхилень варіант відповідно у_і (і=) та х_k (k=) від середньої відповідно та :

.

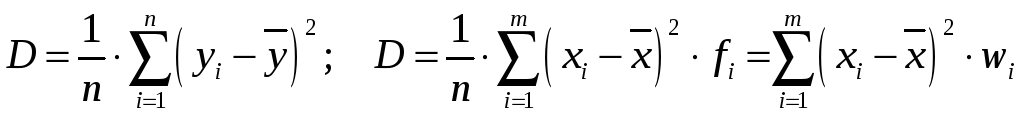Дисперсією і. в. р. називається середня квадратів відхилень середин інтервалів (і=) від середньої :

.

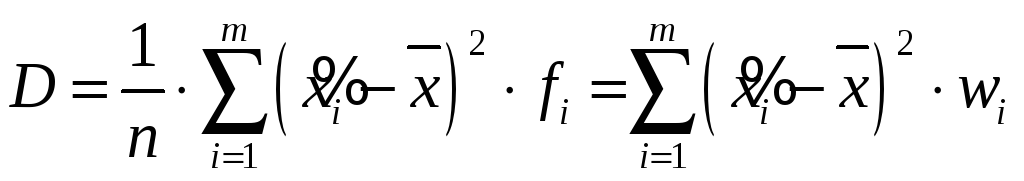Середнім квадратичним відхиленням варіаційного ряду називається квадратний корінь із дисперсії:

(1.7)

Середнім лінійним відхиленням з. в. р. і д. в. р. називається середня модулів відхилень варіант відповідно у_і (і=) та х_k (k=) від середньої відповідно та :

.

Середнім лінійним відхиленням і. в. р. називається середня модулів відхилень середин інтервалів (і=) від середньої :

.

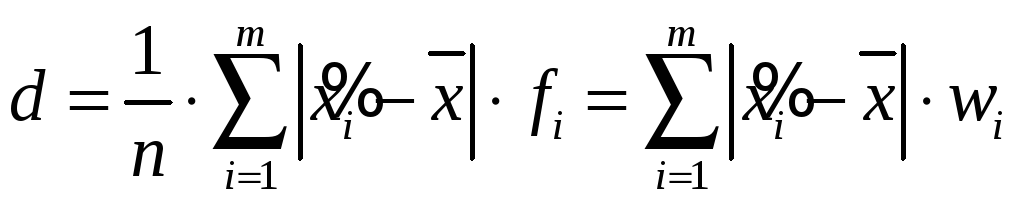Квадратичним (лінійним) коефіцієнтом варіації варіаційного ряду називається відношення середнього квардатичного (лінійного) відхилення до модуля середньої. Може виражатись відношенням або в процентах:

або .

Доведено, що для одного і того ж варіаційного ряду V_d <V_σ; якщо , то розподіл статистичної сукупності має бути близьким до симетричного (див. п. 3.3).

Коефіцієнтом осциляції варіаційного ряду називається відношення розмаху варіації до модуля середньої. Може виражатись відношенням або у процентах:

або .

Величина варіації ознаки в різних рядах розподілу вважається приблизно однаковою, якщо їх відповідні коефіцієнти варіації або осциляції є наближено рівними і навпаки.

3.3. Характеристики форми розподілу

Поняття форми розподілу визначене тільки для д. в. р. та і. в. р. 

Під формою розподілу варіаційного ряду у статистиці розуміють форму його графічних зображень: полігону або гістограми. За своєю формою всі варіаційні ряди розподілу поділяються на: одновершинні і багатовершинні, симетричні та асиметричні, гостроверхі й плосковерхі.

Вершиною розподілу називається така вершина полігону частот або часток, ордината якої більша за ординату однієї з двох сусідніх вершин полігону і не менша за ординату іншої. Багатовершинність розподілу у статистиці зазвичай вважається ознакою кількісної неоднорідності сукупності, що вивчається.

Розподіл називається симетричним (асиметричним), якщо його полігон або гістограма мають (не мають) вісь симетрії, паралельну осі ординат. При цьому полігон частот або часток слід розглядати як сукупність точок без відрізків, що їх сполучають.

У симетричному розподілі рівновіддалені від варіанти (для д. в. р.) або інтервали (для і. в. р.) мають рівні частоти (і частки), а Ме=, для симетричного унімодального розподілу Мо=Ме=. Останні хоча б наближені рівності можуть слугувати попередніми ознаками того, що розподіл скоріш за все має бути майже симетричним.

Для точного встановлення факту симетрії або асиметрії розподілу і вимірювання величини асиметрії необхідно обчислити коефіцієнт асиметрії, який визначається як відношення центрального моменту третього порядку до третього степеня середнього квадратичного відхилення:

As=μ₃/σ³

і обчислюється відповідно для д. в. р. та і. в. р. за формулами:

;

.

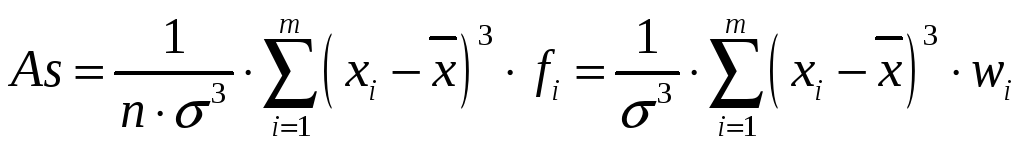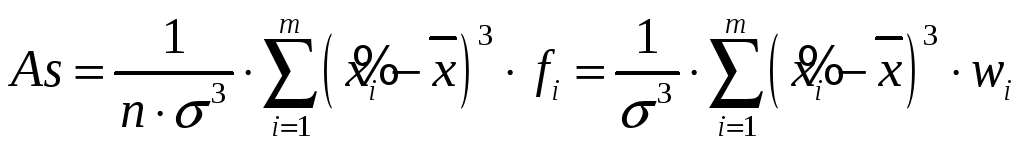Якщо As=0 (As≠0), то розподіл є симетричним (асиметричним). Якщо As>0 (As<0), то асиметрія називається правосторонньою (лівосторонньою) і зазвичай Ме< (<Ме), для унімодального розподілу Мо<Ме< (<Ме<Мо). Останні нерівності можуть служити попередніми орієнтовними ознаками виду асиметрії.

Для вимірювання величини асиметрії прийнято вважати:

• якщо |As|<0,1, то розподіл майже симетричний;

• якщо 0,1≤|As|<0,3, то асиметрія є незначною (або низькою, або слабкою);

• якщо 0,3≤|As|<0,5, то асиметрія є помірною (або середньою);

• якщо 0,5≤|As|, то асиметрія є значною (або високою, або сильною).

Гостроверхість чи плосковерхість розподілу встановлюється відносно теоретичного нормального розподілу неперервних випадкових величин з тим же значенням дисперсії σ² і визначається за допомогою коефіцієнта ексцесу, який у статистиці визначається як відношення центрального моменту четвертого порядку до четвертого степеня середнього квадратичного відхилення: Ех=μ₄ /σ⁴ і обчислюється для д. в. р. та і. в. р. за формулами відповідно:

;

.

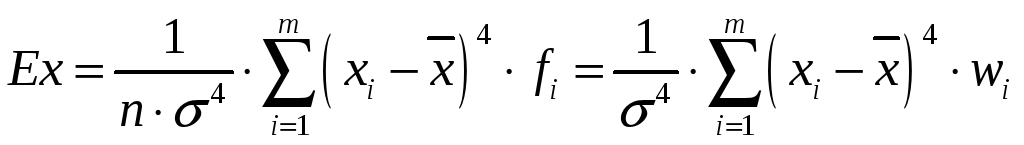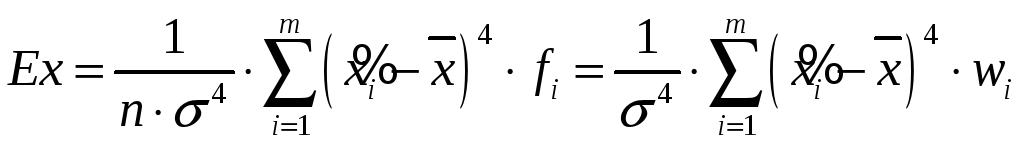Для теоретичного нормального розподілу Ех=3, тому якщо Ех>3 (Ех<3), то розподіл вважається гостроверхим (плосковерхим). Величина гостро- чи плосковерхості в статистиці не вимірюється.