2. Метод аналітичного групування (п. 2.2).

Розділимо задану сукупність пар (х_і; у_і) на групи за факторною ознакою Х, використавши поділ, вже зроблений у таблиці 3.4. В результаті одержимо групи (тобто, інтервали) пар (х_і; у_і), наведені в таблиці 3.5.

Для кожної з 3-х груп обчислимо групові середні та (k=) і приймаємо за значення х_k факторної ознаки Х:

х₁ =(50,3+40,8+55,0+44,0+67,7+65,9)≈53,95;

(203,1+200,3+242,7+228,0+308,5+257,0)≈239,93.

Аналогічно обчислюємо х₂=102,27; =342,84; х₃=169,40; =434,10.

Таблиця 3.5.

Робоча таблиця

№ гру-пи (k)	Інтервал значень Х	Пари (хі; уі)
		і	1	2	3	4	5	6	7	8	9	10
1	до 70	хі	50,3	40,8	55,0	44,0	67,7	65,9	–	–	–	–
		уі	203,1	200,3	242,7	228,0	308,5	257,0	–	–	–	–
2	70 ; 140	хі	79,6	89,4	72,3	110,5	120,0	131,7	92,8	136,0	97,0	93,4
		уі	308,6	316,2	280,1	358,9	360,6	365,4	340,8	422,0	362,0	310,8
3	140 і більше	хі	178,3	143,7	165,4	190,2	–	–	–	–	–	–
		уі	420,0	380,7	425,4	510,3	–	–	–	–	–	–

Знайдені значення х_k факторної ознаки Х та відповідні середні значення результативної ознаки Y заносимо в таблицю 3.6, яка й буде являти собою лінію регресії, задану таблично:

Таблиця 3.6

Таблично задана лінія регресії

k	xk
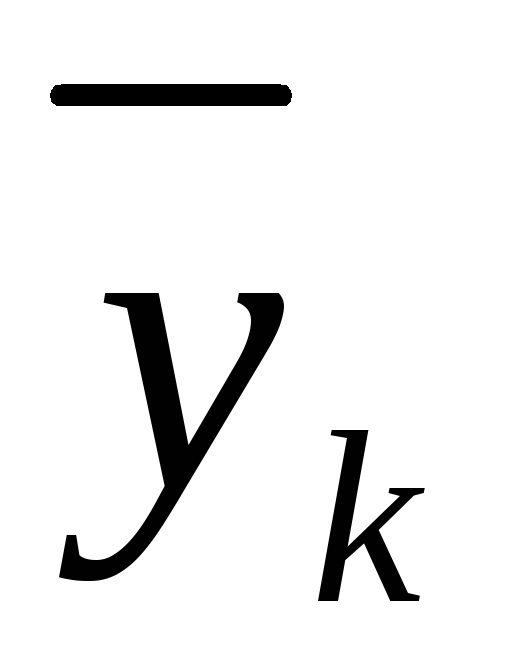
1 2 3	53,95 102,27 169,40	239,93 342,84 434,10

Для наочності побудуємо графік лінії регресії. Для цього в прямокутній системі координат зобразимо точки з координатами (x_k; ) (тобто кореляційне поле) і послідовно сполучимо їх відрізками прямих (див. рис.3.7).

Із аналізу таблиці 3.6 і графіка (рис. 3.7) можна зробити такий висновок: більшим витратам на утримання відповідають більші перерахування до бюджету, що підтверджує попередній висновок про можливість існування прямого зв’язку між Х та Y, зроблений за результатами комбінаційного групування. При цьому із вигляду графіка можна припустити, що зростання Y має, можливо, сповільнений характер.

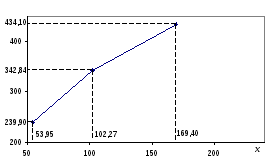
Рис. 3.7. Графік таблично заданої лінії регресії

3. Метод дисперсійного аналізу (п. 2.3)

Усю сукупність 20-ти пар (х_і; у_і), що вивчається, розділимо за факторною ознакою на 3 групи, використавши поділ, зроблений у таблиці 3.5. За формулою (3.1) обчислимо загальну середню для всієї сукупності значень у_і (і=):

.

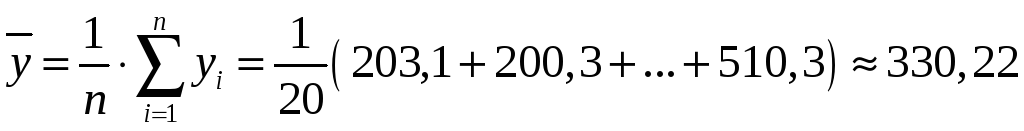За формулою (3.3) обчислимо загальну дисперсію ознаки Y:

.

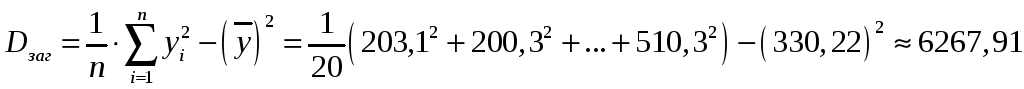За формулою (3.6) обчислимо міжгрупову дисперсію, використавши раніше знайдені значення групових середніх (табл. 3.6) і частот f_k (табл. 3.4):

.

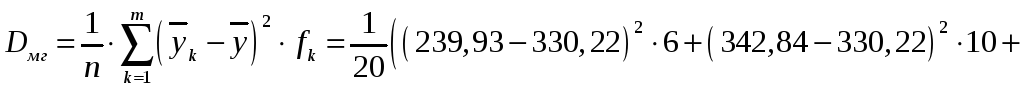
За формулою (3.8) обчислюємо спостережене значення кореляційного відношення:

звідки витікає, що 74,7 % загальної варіації ознаки Y пов’язано з варіацією ознаки Х, а це свідчить про можливість існування залежності Y від Х.

Для формального підтвердження або спростування даного припущення знайдемо критичне значення величини η² для рівня значущості . За таблицею критичних значень (додаток 2) для степенів вільності k₁=m–1=3–1=2, k₂=n–m=20–3=17 знаходимо = =0,297. Оскільки , то з імовірністю =0,95 можна вважати, що Y істотно залежить від Х. Для оцінки щільності зв’язку застосовуємо правило трисекції: 0,7+ 0,3=0,508; 0,3+ 0,7=0,789. Оскільки  [0,7+ 0,3; 0,3+ 0,7], то щільність зв’язку будемо вважати помірною.