2. Метод аналітичного групування

а) може застосовуватись у випадках, коли факторна ознака є атрибутивною або варіаційною, а результативна – тільки варіаційною;

б) дає можливість тільки припускати наявність або відсутність зв’язку, а також визначати його напрям (якщо факторна ознака є ранговою атрибутивною або варіаційною) та можливий вид і характер залежності (останнє – за умови варіаційної факторної ознаки).

в) не дає можливості формально перевіряти істотність та оцінювати щільність зв’язку.

Для проведення аналітичного групування сукупність, що вивчається, поділяється на групи (для варіаційної ознаки − на інтервали) за факторною ознакою. При цьому число т груп може вибиратись дослідником на його власний розсуд. Для варіаційної факторної ознаки ширина інтервалів вибирається дослідником на його розсуд, але бажано, щоб інтервали були кількісно однорідними і для виявлення характеру залежності необхідно, щоб m3. Для кожного і-го інтервалу знаходяться групові середні та , після чого приймаються за значення х_і фактора Х. Якщо при проведенні групування використати поділ, вже зроблений у таблиці 3.1, то одержимо таку, наприклад, лінію регресії, задану таблично (табл. 3.2):

Таблиця 3.2

Лінія регресії, задана таблично

хі	х1	х2	…	хт
			…

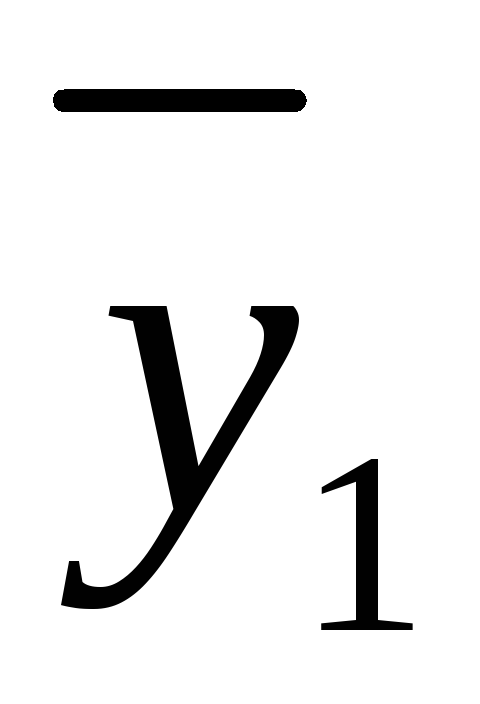
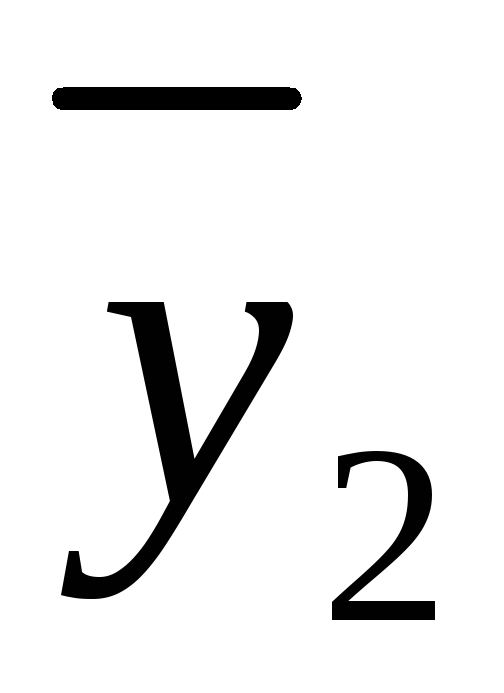
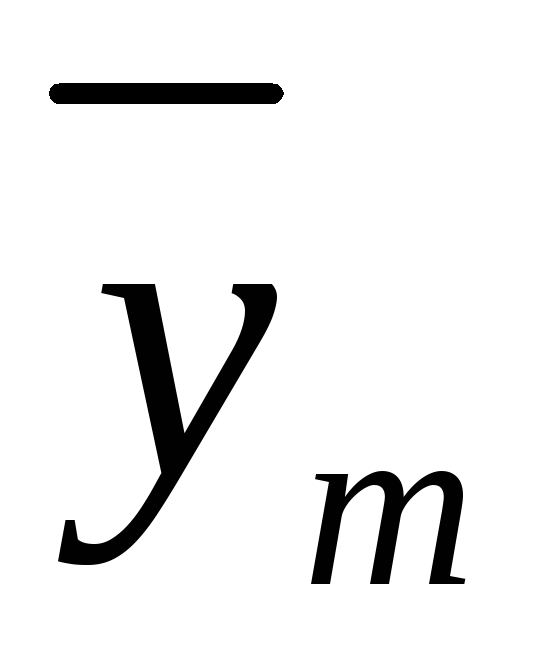
Для більшої наглядності можна побудувати графік лінії регресії, який являє собою сукупність точок з координатами (х_і; ), побудованих у прямокутній системі координат хо (кореляційне поле) і послідовно сполучених відрізками прямих. Якщо, наприклад, цей графік буде мати вигляд, зображений на рис. 3.1, то є підстави для висновку: значення Y прискорено спадають зі зростанням Х (залежність Y від Х є зворотною нелінійною).

Р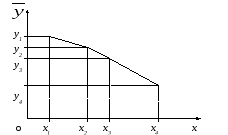 ис. 3.1. Лінія регресії, задана графічно.

Всі основні види і характери залежності зображено на рисунках 3.2 – 3.5:

Р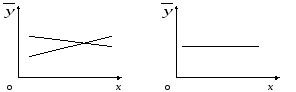 ис. 3.2. Рівномірна пряма (––) Рис. 3.3. Y не залежить від Х

та зворотна (….) залежності

Р ис. 3.4. Прискорені зростання Рис. 3.5. Уповільнені зростання

(––) та спадання (….) (––) та спадання (….)

3. Метод дисперсійного аналізу.

а) може застосовуватись у випадках, коли факторна ознака є атрибутивною або варіаційною, а результативна – тільки варіаційною;

б) дає можливість формально перевіряти істотність звязку та оцінювати його щільність;

в) не дає можливості визначати напрям, характер та можливий вид залежності.

Для реалізації методу необхідно:

1. Усю сукупність п пар (х_і; у_і), що вивчається, розділити за факторною ознакою на т груп (для варіаційної ознаки − на m інтервалів) з обсягом (або частотою) f_k 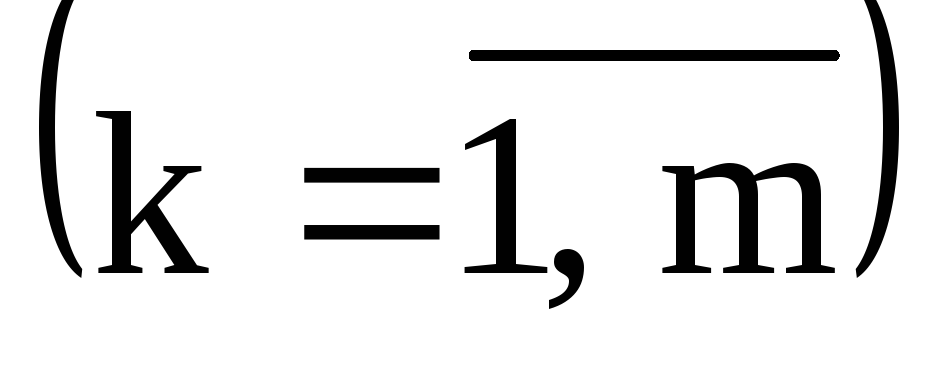кожної групи. При цьому число груп дослідник вибирає суб’єктивно на свій власний розсуд. Для варіаційної факторної ознаки ширина інтервалів обирається дослідником теж суб’єктивно, але бажано, щоб інтервали були кількісно однорідними і т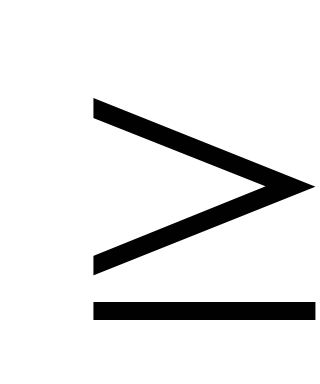3.

2. Обчислити загальну середню результативної ознаки Y для всієї сукупності:

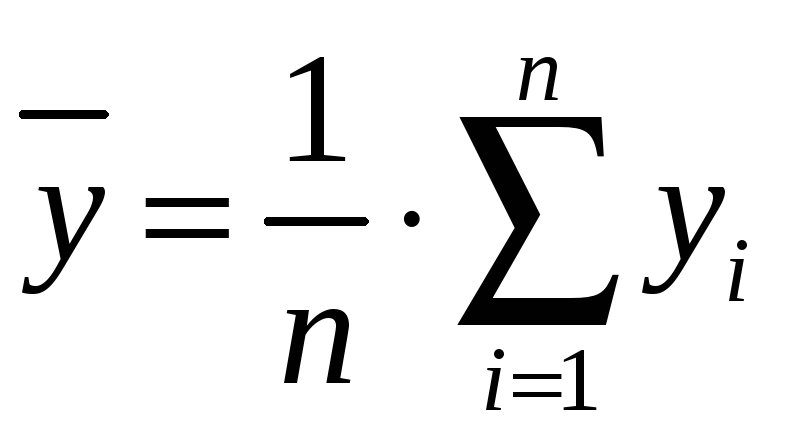(3.1)

та групові середні для кожної k-ї групи :

. (3.2)

3. Обчислити загальну дисперсію ознаки Y для всієї сукупності:

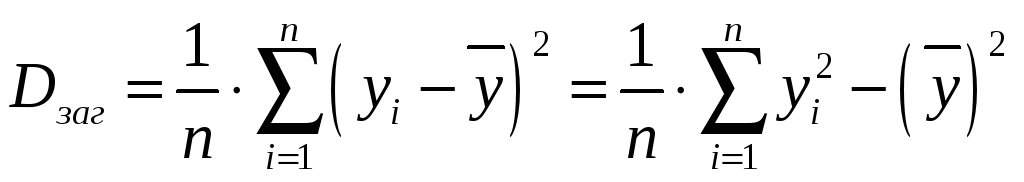, (3.3)

групові дисперсії для кожної k-ї групи:

, (3.4)

середню зважену з групових дисперсій:

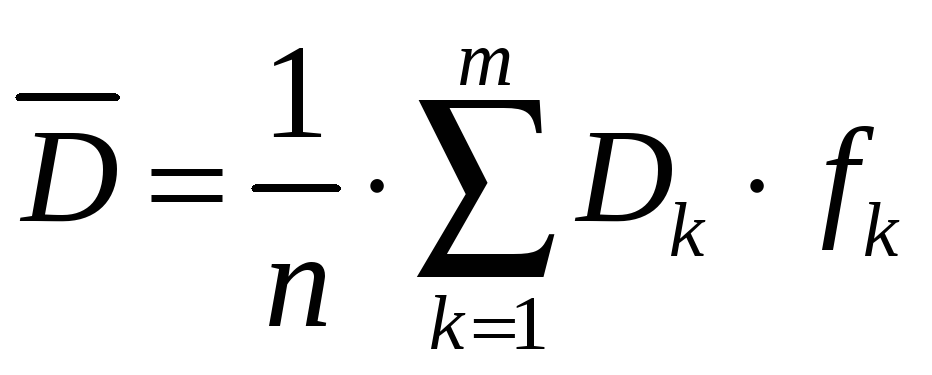, (3.5)

де f_k – частота k-ї групи,

міжгрупову дисперсію:

. (3.6)

Для вищенаведених величин існує правило додавання дисперсій:

. (3.7)

4. Обчислити величину

, (3.8)

яка називається кореляційним відношенням і є числовою мірою щільності та істотності зв’язку в дисперсійному аналізі. Очевидно, що  [0; 1]. Міжгрупова дисперсія характеризує частину загальної варіації ознаки Y, пов’язану з варіацією групувальної (тобто, факторної) ознаки Х, а значить і залежність Y від Х: чим ближче до (a η², відповідно, до 1), тим зв’язок тісніший і навпаки.

5. За таблицями критичних значень величини η² (додаток 2) знайти її критичне значення , яке залежить від рівня значущості α та степенів вільності k₁=m‑1 i k₂=n‑m. У статистичній практиці величина α вибирається зазвичай рівною 0,05 або 0,10 і являє собою імовірність оцінити зв’язок як істотний при його фактичній відсутності.

6. Порівняти обчислене за формулою (3.8) спостережене значення з критичним і зробити висновок: якщо >, то з імовірністю γ=(1–α) зв’язок вважається істотним (тобто, існуючим) і навпаки.

7. Для оцінки щільності зв’язку (якщо, звичайно, попередньо буде встановлена його істотність) можна керуватись правилом трисекції: будемо вважати зв’язок:

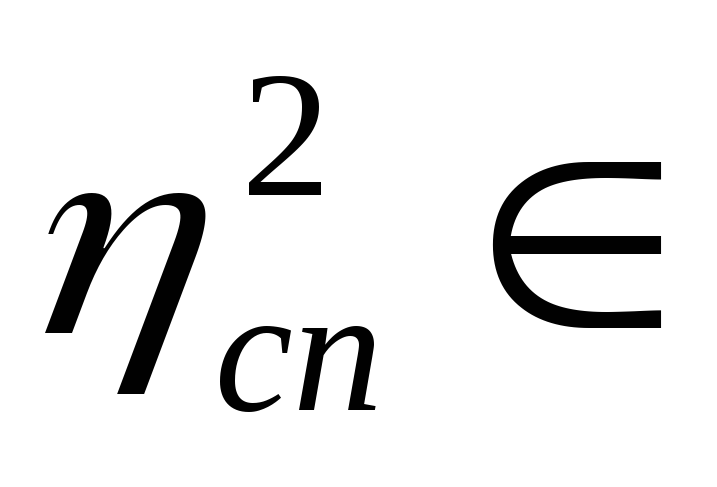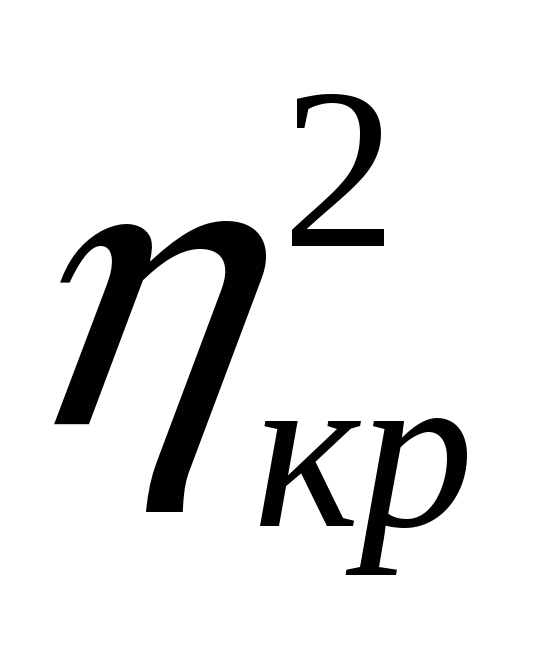• щільним для  (0,3+ 0,7; 1];

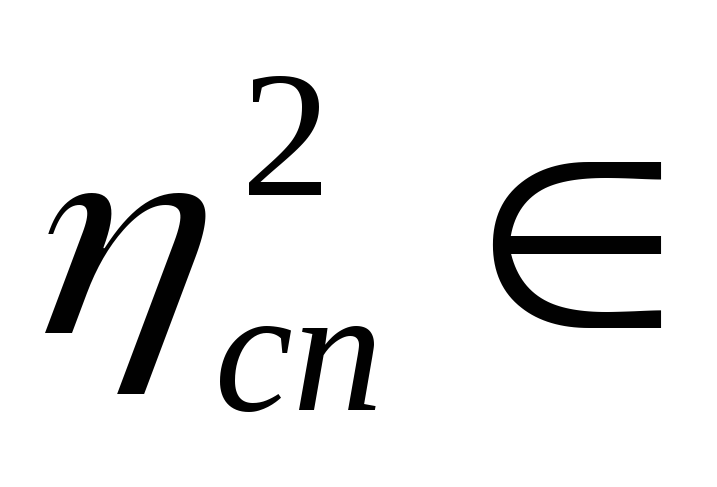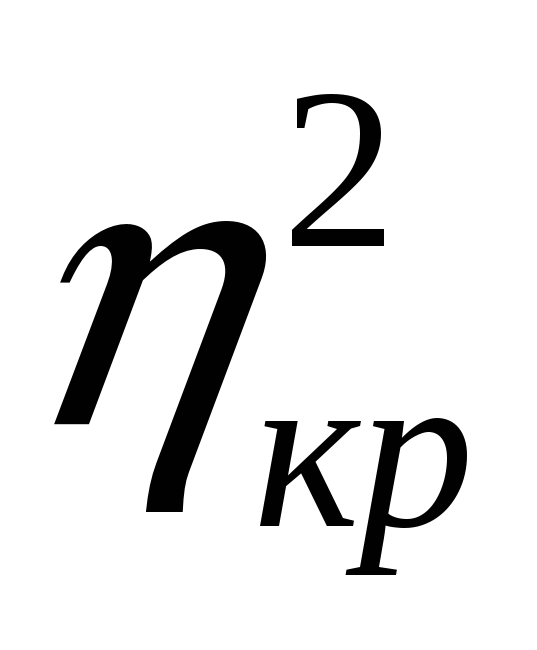• помірним для  (0,7+ 0,3; 0,3+ 0,7];

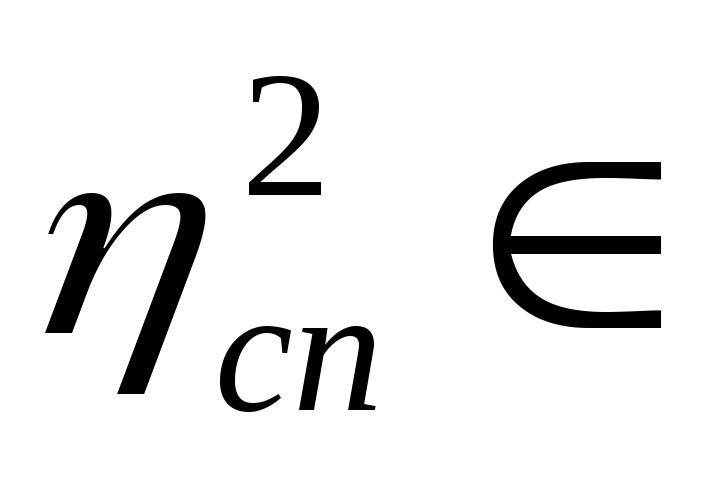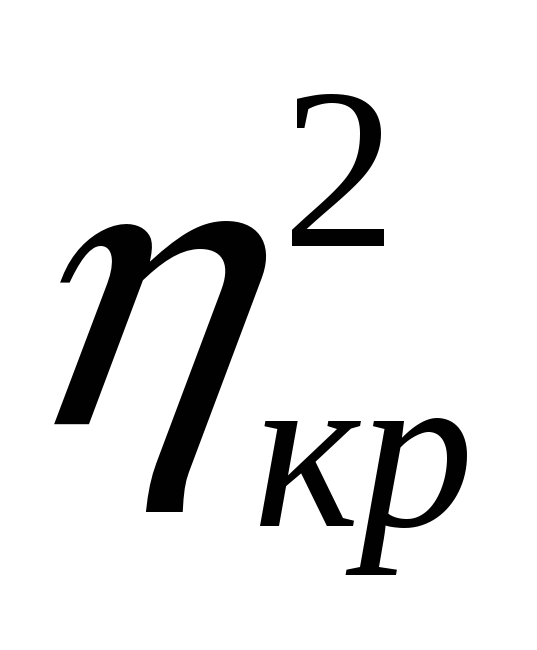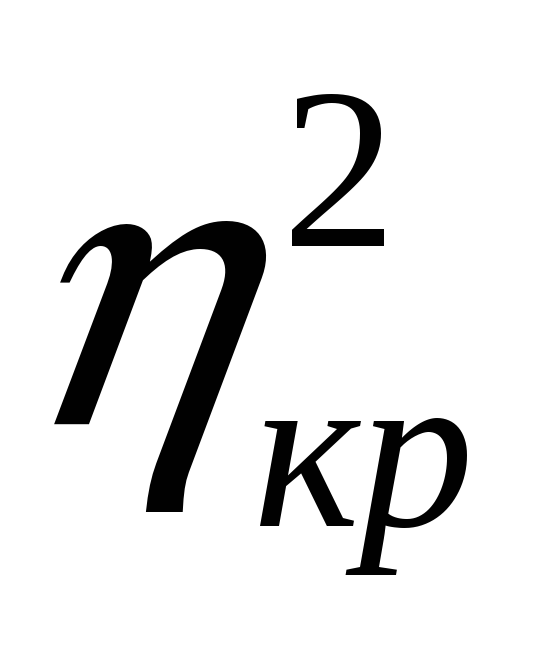• слабким для  (; 0,7+ 0,3].