Аудиторные задания

Найти обратную матрицу:

№99. . Ответ: .

№100. 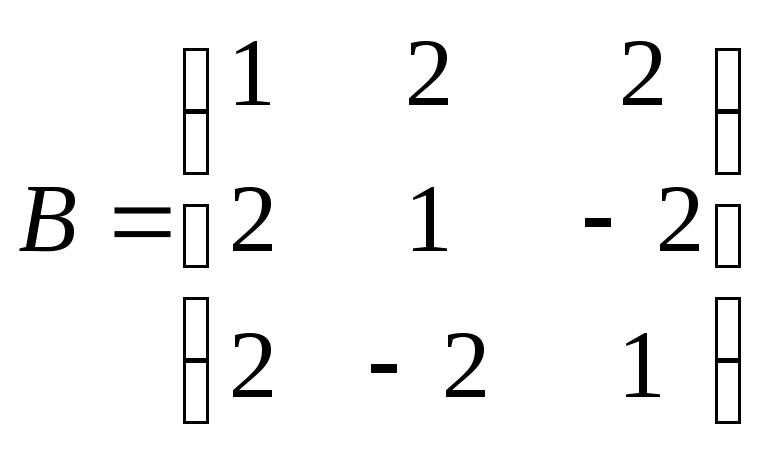. Ответ: .

Найти ранг матрицы:

№101. . Ответ: 2.

№102. 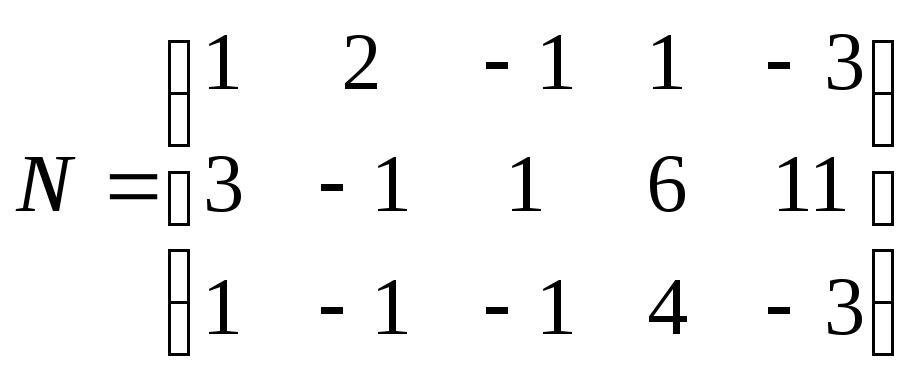. Ответ: 3.

Найти обратную матрицу:

№103. . Ответ: .

№104. . Ответ: .

Найти ранг матрицы:

№105. . Ответ: 3.

№106. . Ответ: 3.

Решить уравнение

№107. . Ответ: .

№108. . Ответ: .

Домашние задания

Найти обратную матрицу

№109. D=. Ответ: .

№110. С=. Ответ: .

Найти ранг матрицы:

№111. . Ответ: 3.

№112. . Ответ: 3.

№113. . Ответ: 2.

№114. . Ответ: 3.

Решить уравнение:

№116. 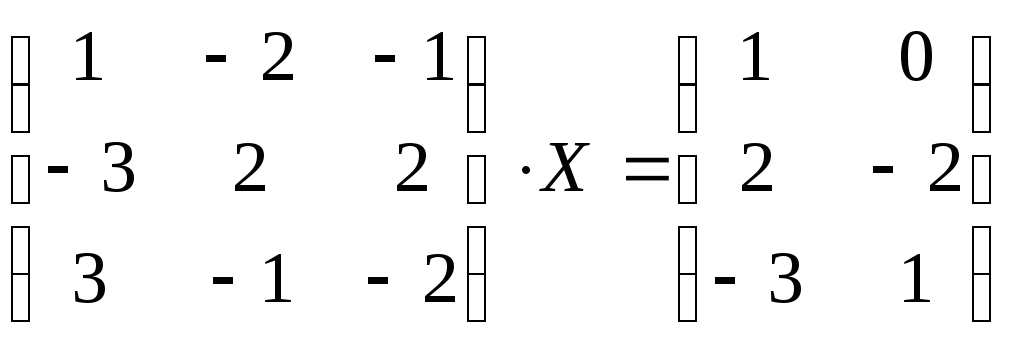. Ответ: .

№108. . Ответ: Х не существует.

Дополнительные задания

Найти обратную матрицу:

№117. . Ответ: .

№118. 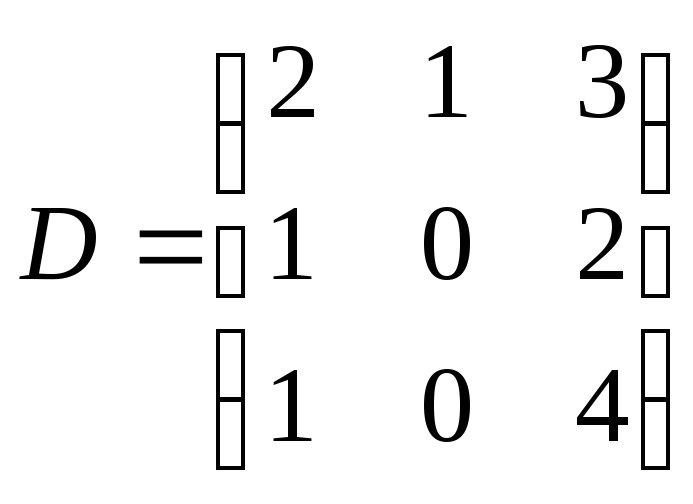. Ответ: .

Найти ранг матрицы:

№119. . Ответ: 2.

№120. . Ответ: 3.

№121. . Ответ: 3.

№122. . Ответ: 2.

Найти ранг матрицы при различных значениях параметра а:

№123. .

Ответ: r=3 при а=; r=4 при а.

№124. . Ответ: r=2 при а=3; r=3 при а3.

Решить уравнения:

№125. . Ответ: .

№126. . Ответ: .

№127. . Ответ: .

№128. .

Ответ: .

Выполнить действия:

№129. .

№130. .

№131. .

Решение типового варианта индивидуального домашнего задания «Определители. Матрицы»

Задание 1. Для определителя 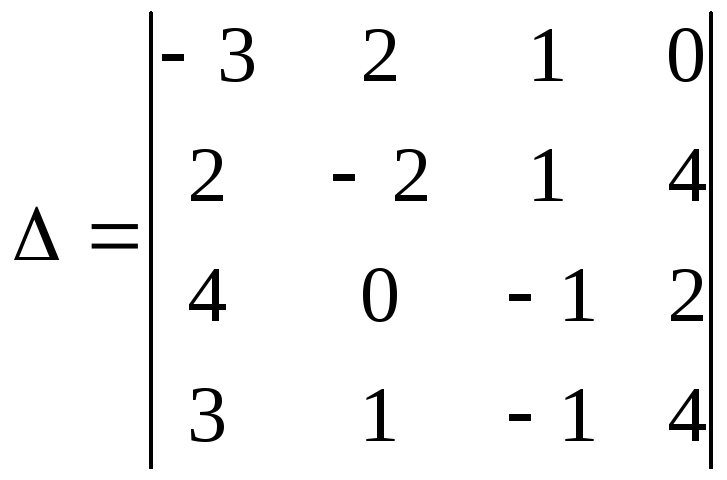найти миноры и алгебраические дополнения элементов а_i2, a_3j. Вычислить определитель : а) разложив его по элементам i-й строки; б) разложив его по элементам j–столбца; в) получив предварительно нули в i-й строке. (i=1; j=2).

► Находим миноры для элементов а₁₂ и а₃₂:

М₁₂== – 8–16+6+12+4 – 16= –18;

М₃₂== –12+12 –12 – 8= –20.

Алгебраические дополнения элементов а₁₂ и а₃₂ равны:

А₁₂=(–1)¹⁺²М₁₂= – (–18)=18;

А₃₂=(–1)³⁺²М₃₂= – (–20)=20.

а) Вычислим данный определитель по элементам первой строки:

=

=–3–2+1=

= –3(8+2+4 – 4) – 2(– 8– 16+6+12+4 – 16)+(16 – 12 – 4+32)=38;

б) Разложим определитель по элементам второго столбца:

а₁₂А₁₂+а₂₂А₂₂+а₃₂А₃₂+а₄₂А₄₂=

= –2 – 2+1=

= – 2( – 8+6 – 16+12+4 – 16) –2(12+6 – 6 – 16)+

+( – 6+16 – 12 – 4)=38;

в) Вычислим определитель, получив предварительно нули в первой строке. Используем следствие свойства 4. Умножим третий столбец определителя на 3 и прибавим к первому, затем умножим на –2 и прибавим ко второму. Тогда в первой строке все элементы, кроме третьего, будут нулями. Разложим полученный таким образом определитель по элементам первой строки и вычислим его:

===

== – (– 56+18) =38. 

Задание 2. Даны две матрицы А=, В=. Найти: а) АВ; б) В^ТА; в) А^-1; г) АА^-1; д) А^-1А.

► а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Имеем:

С=АВ==

==;

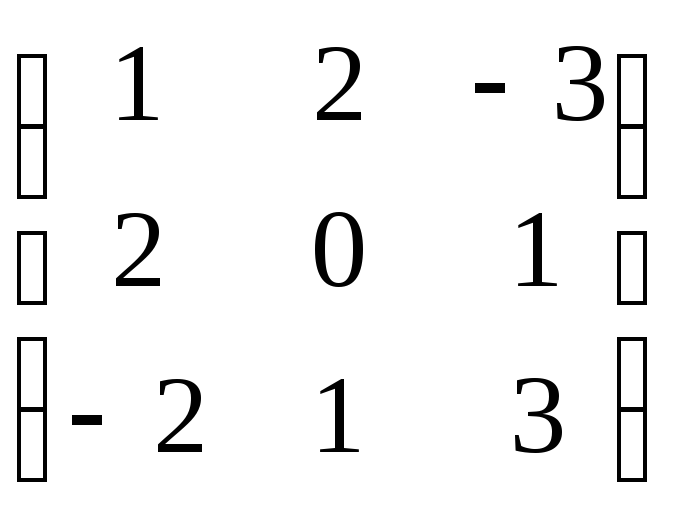б) Найдём В^Т=.

Вычислим В^ТА==.

в) Обратная матрица А^-1 матрицы А имеет вид:

А^-1=, где det A==390, т.е. матрица А^-1 существует. Найдём алгебраические дополнения каждого элемента:

А₁₁== – 8; А₂₁= – =2; А₃₁==1;

А₁₂=–=5; А₂₂== –11; А₃₂= – =14;

А₁₃==7; А₂₃= – =8; А₃₃==4.

Тогда А^-1==;

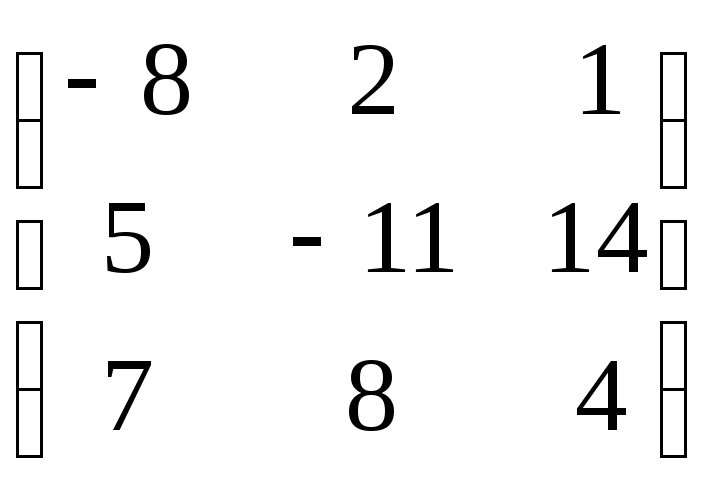г) АА^-1===Е;

д) А^-1А===Е,

т.е. обратная матрица найдена, верно. 

Занятие 4

Системы линейных алгебраических уравнений (СЛАУ). Основные понятия. Теорема Кронекера-Капелли. Решение СЛАУ матричным методом. Формулы Крамера. Метод Гаусса. Общее решение СЛАУ

Цели

Знать:

• Основные определения, связанные с понятием систем линейных алгебраических уравнений (СЛАУ);

• теорему Кронекера-Капелли;

• основные методы решения СЛАУ.

Уметь:

• Применять теорему Кронекера-Капелли при исследовании решения СЛАУ;

• решать СЛАУ матричным методом, по формулам Крамера; методом Гаусса и Жордано-Гаусса;

• находить общее и частное решение СЛАУ.

Теорема Кронекера-Капелли. Для того чтобы система линейных алгебраических уравнений относительно n неизвестных х₁, х₂, …, x_n была совместна (имела решение), необходимо и достаточно, чтобы ранг основной матрицы заданной системы и ранг расширенной матрицы заданной системы были равны, т.е. Rang A=Rang=r.

Если RangA=Rang=r и r=n (n — число неизвестных), то заданная система имеет единственное решение.

Если r<n , то система имеет бесконечно много решений, зависящее от (n – r) произвольных параметров.

Постановка задачи: Используя теорему Кронекера-Капелли исследовать систему линейных алгебраических уравнений на совместность.

План решения: 1. Записать расширенную матрицу заданной системы;

2. найти ранг полученной матрицы;

3. используя теорему Кронекера-Капелли сделать вывод.

№17. Исследовать систему на совместность

► 1) Составим расширенную матрицу: .

2) Методом элементарных преобразований найдём ранги расширенной и основной матрицы

=, т.е. Rang A=2; Rang=3, следовательно, т.е. система несовместна. ◄

Постановка задачи: решить СЛАУ матричным методом.

План решения: 1. Используя теорему Кронекера-Капелли исследовать систему линейных алгебраических уравнений на совместность;

2. записать СЛАУ в матричной форме: АХ=В, где — основная матрица, — матрица-столбец из неизвестных x_j, — матрица-столбец свободных членов b_i.;

3. найдём обратную матрицу для основной матрицы;

4. для отыскания решения системы воспользуемся формулой

(4);

5. записать ответ.

№18. Проверить совместимость системы и в случае совместимости решить её матричным методом:

► 1) Проверим совместимость системы. Составим основную матрицу системы , Rang A=3. Составим расширенную матрицу системы , Rang=3. Следовательно, система совместна. Т.к. r=3, и n=3, то система имеет единственное решение;

2) Запишем СЛАУ в матричной форме , , ;

3) найдем обратную матицу для матрицы А:

;

4) согласно формуле (4) имеем:

;

.

5) решение системы: х₁=1; х₂=1; х₃=1. ◄

Постановка задачи: Проверить совместимость системы и в случае совместимости решить её по формулам Крамера.

План решения: 1. Используя теорему Кронекера-Капелли проверить СЛАУ на совместность;

2. найти определитель основной матрицы системы, а затем вспомогательные определители;

3. воспользоваться формулами Крамера

(5),

где — определитель, полученный из определителя системы путём замены i-го столбца столбцом свободных членов, стоящих в правой части уравнений;

4. записать ответ.

№19. Проверить совместимость системы и в случае совместимости решить её по формулам Крамера:

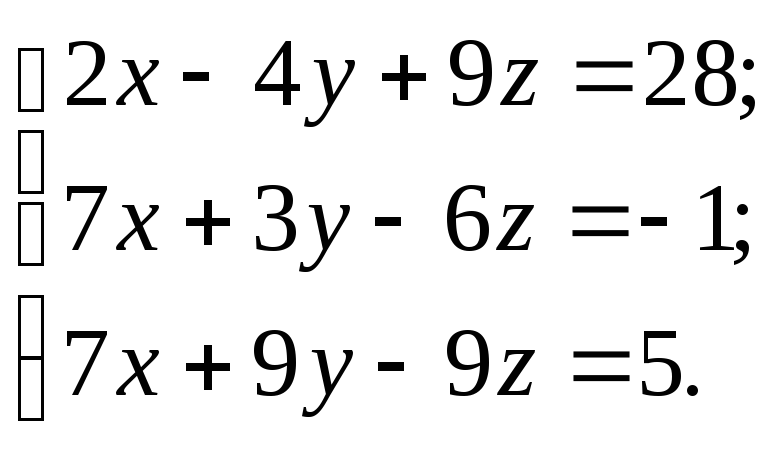
► 1) Проверим совместимость системы. Основная матрица имеет Rang A=3; расширенная матрица системы имеет Rang=3, т.е. система совместна. Так как r=3, и n=3, то система имеет единственное решение;

2) Найдём основной и вспомогательные определители системы:

, ; ;

;

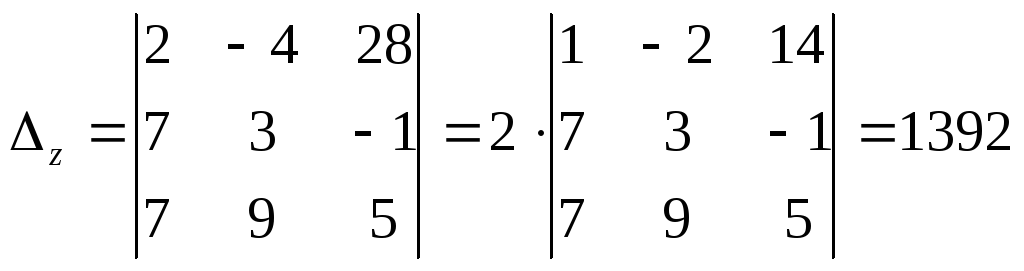3) По формулам Крамера (5) имеем:

; ; ;

4) решение системы: x=2; y=3; z=4. ◄

Элементарные преобразования

системы линейных алгебраических уравнений

1. перестановка местами двух или нескольких уравнений;

2. умножение обеих частей одного из уравнений на любое число, отличное от нуля;

3. прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число;

4. вычёркивание нулевой строки.

Постановка задачи: Проверить совместимость системы и в случае совместимости решить её методом Гаусса

План решения: 1. Используя теорему Кронекера-Капелли проверить СЛАУ на совместность;

2. выполнить прямой ход метода Гаусса: используя элементарные преобразования СЛАУ преобразовать систему в эквивалентную треугольного вида;

3. выполнить обратный ход метода Гаусса: из последнего уравнения определить неизвестное, из предыдущего уравнения находим еще одно — предпоследнее и т.д. Таким образом, подставляя полученные величины неизвестных, мы последовательно найдём все решения системы;

4. записать ответ.

№20. Проверить совместимость системы и в случае совместимости решить её методом Гаусса:

► 1) Проверим совместимость системы. Ранг основной матрицы системы , RangA=3; ранг расширенной матрицы , Rang=3. Ранги основной и расширенной матрицы равны, следовательно, система совместна. Т.к. r=3, и n=3, то система имеет единственное решение;

2) Прямой ход. Выполним преобразования. Первое уравнение оставим без изменения. Для того чтобы избавиться от первого неизвестного во втором и третьем уравнениях, к ним прибавим первое, умноженное на –2 в первом случае и на –1 во втором

Теперь избавимся от второго неизвестного в третьем уравнении. Для этого второе уравнение умножим на –2 и прибавим к третьему. Получили эквивалентную систему треугольного вида:

3) Обратный ход. Решаем данную систему снизу вверх. Из третьего уравнения находим х₃=3 и, подставляя его во второе уравнение, находим х₂=2. Подставив найденные неизвестные в первое уравнение, получим х₁=1;

4) Решение системы: х₁=1; x₂=2; x₃=3. ◄

▼ Неизвестное x_k называется разрешённым, если какое-нибудь уравнение системы содержит x_k с коэффициентом единица, а во всех остальных уравнениях системы неизвестное x_k не содержится, т.е. содержится с коэффициентом нуль. ▲

▼ Система уравнений называется разрешённой, если каждое уравнение содержит разрешённое неизвестное. ▲

▼ Общим решением совместной системы уравнений называется равносильная система, в которой разрешённые неизвестные выражены через свободные. ▲

▼ Если в общем решении свободным неизвестным придать какие-нибудь числовые значения, то получим решение данной системы, называемое частным. ▲

№21. Решить систему:

► Исследуем систему на совместимость: найдем ранги основной матрицы системы и расширенной матрицы:

.

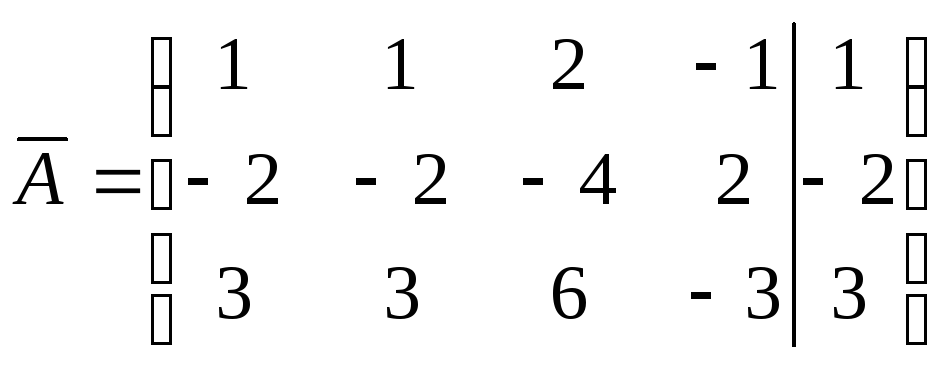
Следовательно, RangA=Rang=1, т.е. система совместна. Так как n=4, то система имеет бесконечно много решений. Найдём количество свободных элементов: r – n =4 – 1=3.

Используя последнюю матрицу можно составить систему:

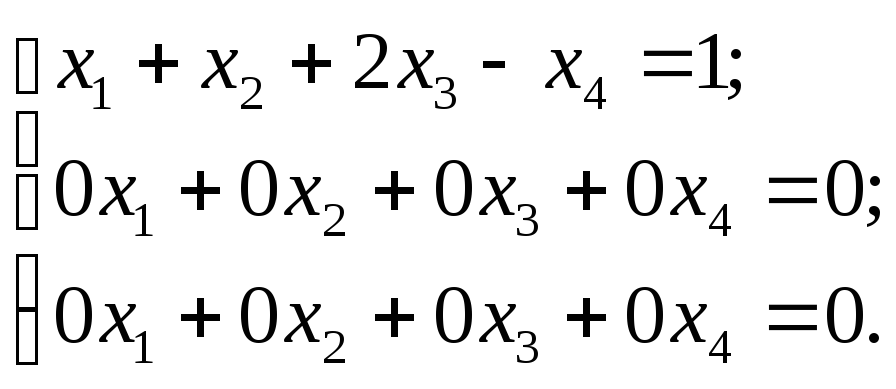
которая может быть представлена в виде

х₁+х₂+2х₃ – х₄=1,

т.к. последние два уравнения — истинные тождества. В данном уравнении х₁ и х₂ — разрешённые элементы. Т.к. свободных элементов три, то общее решение системы имеет вид:

Выбрав t=2, v=1, s= –3, получим частное решение системы:

х₁= –6; x₂=2; x₃=1; х₄= –3. ◄

№22. Решить систему методом Жордана-Гаусса

► 1. Составим расширенную матрицу системы

≈.

Преобразуем данную матрицу к диагональному виду. Для этого в качестве разрешающего элемента удобно взять элемент, равный 1, например, а₁₁=1≠0. Делим элементы разрешающей строки на разрешающий элемент, т.к. он равен единице, то элементы разрешающей строки не меняются. Разрешающую переменную следует исключить из остальных уравнений, поэтому в новой матрице все элементы (элементы новых матриц обозначим со штрихами) первого столбца кроме а₁₁ равны нулю. Другие элементы новой матрицы находим по правилу прямоугольника:

, и т.д.

Новая матрица имеет вид: .

2. В качестве разрешающего элемента в данной матрице берём не равный нулю элемент из любой строки, кроме первой, например, а₂₂= – 5. Делим элементы разрешающей строки на (–5): .

Элементы второго столбца, кроме а₂₂, берём равными нулю, а остальные элементы вычисляем по правилу прямоугольника: , и т.д.

Новая матрица имеет вид: .

Для удобства вычислений преобразуем полученную матрицу

.

Выберем в качестве ведущего элемент а₃₃=1. Элементы третьего столбца кроме а₃₃, берём равными нулю, а остальные элементы вычисляем по правилу прямоугольника: ,

и т.д.

Новая матрица имеет вид: .

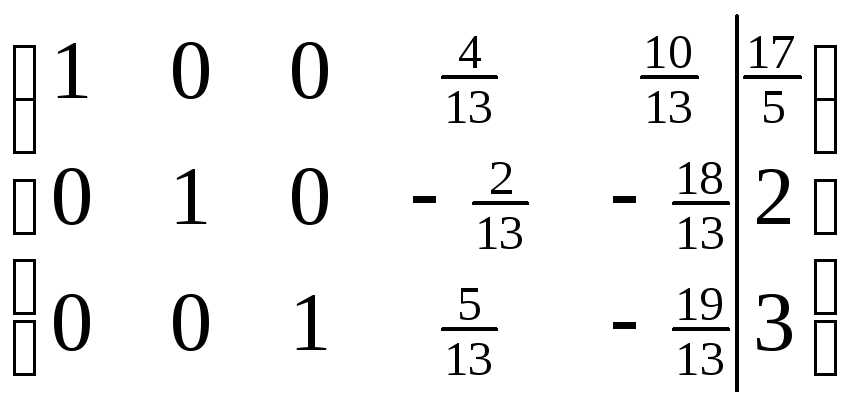3. Так как все строки матрицы уже брались в качестве разрешающих, выписываем систему уравнений, соответствующую последней матрице:

В качестве разрешающих элементов удобно выбрать х₁; х₂ и х₃:

Полагая , получим общее решение системы:

k, p . ◄