Домашние задания

Вычислить определитель:

№47. . Ответ: 0.

№48. . Ответ: cos2x.

№49. . Ответ: .

№50. . Ответ: 4a b.

№51. . Ответ: –2b³.

№52. . Ответ:71.

№53. . Ответ: –12.

Решить уравнения:

№54. . Ответ: х=12.

№55. 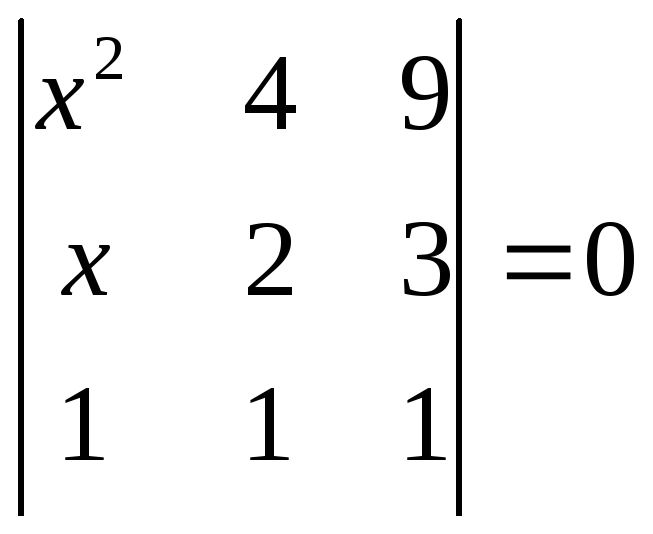. Ответ: х₁=2; х₂=3.

Решить неравенства:

№56. . Ответ: x>–10.

№57. . Ответ: x<–3.

№58. . Ответ: x>2.

№59. Дан определитель . Найти М₂₂, М₁₃, А₁₂; А₃₁.

Вычислить определитель:

№60. . Ответ: 0.

№61. . Ответ: 9.

№62. . Ответ: 160.

Дополнительные задания

Вычислить определитель:

№63. . Ответ: 5.

№64. . Ответ: 0.

№65. . Ответ: 0.

№66. . Ответ: 1.

№67. . Ответ: .

№68. . Ответ: 1.

№69. . Ответ: sin²x.

№70. . Ответ: 0.

№71. . Ответ: 0.

№72. . Ответ: 0.

№73. . Ответ: –36.

№74. . Ответ: –32.

№75. . Ответ: 0.

№76. . Ответ: –8.

№77. . Ответ: 2(a d–b c).

№78. . Ответ: а х².

Решить уравнения:

№79. . Ответ: х=.

№80. . Ответ: х₁=0; x₂=1; x₃= –3.

№81. . Ответ: .

№82. . Ответ: х₁=2; .

№83. 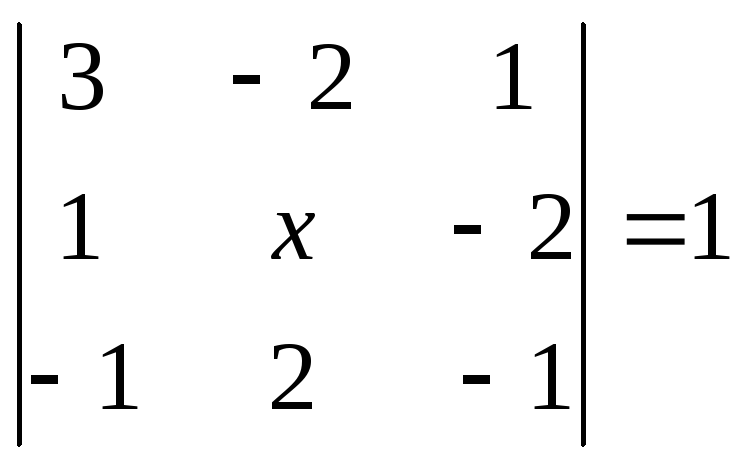. Ответ: х=.

№84. . Ответ: х=–3.

№85. . Ответ: х₁=2; х₂=3.

Решить неравенства:

№86. . Ответ: x>3.

№87. . Ответ: x>–10.

№88. . Ответ: .

№89. . Ответ: .

Вычислить определитель:

№90. . Ответ: 0.

№91. . Ответ: 27.

№92. . Ответ: –492.

№93. . Ответ: 54.

№94. . Ответ: 16.

№95. . Ответ: 48.

№96. . Ответ: 26.

№97. . Ответ: –7.

№98. . Ответ: 394.

Занятие 3

Невырожденные матрицы. Обратная матрица. Методы нахождения обратной матрицы. Ранг матрицы. Вычисление ранга матрицы

Цели

Знать:

• Определения невырожденной обратной матрицы, ранга матрицы;

• свойства обратной матрицы и ранга матрицы.

Уметь:

• Находить обратную матрицу методом союзной матрицы и методом Жордановых исключений;

• решать матричные уравнения;

• вычислять ранг матрицы методом окаймляющих миноров и с помощью элементарных преобразований.

Постановка задачи: найти для квадратной матрицы А обратную, методом союзной матрицы.

План решения: 1. Вычислить определитель матрицы А;

2. найти союзную матрицу 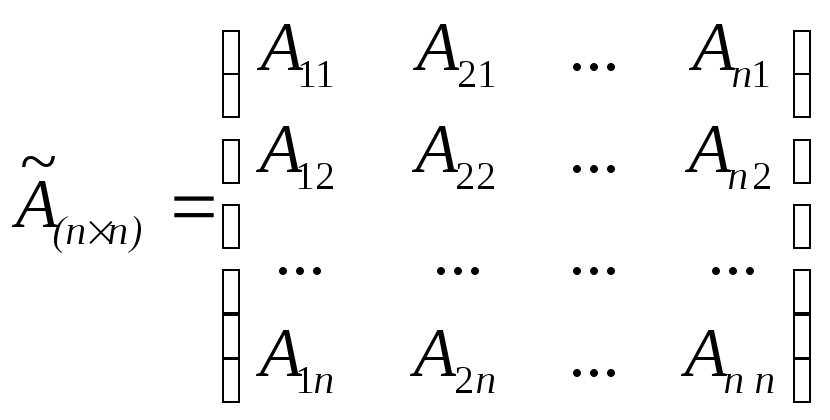, где A_ij — алгебраические дополнения элемента а_ij данной матрицы А (оно определяется также, как и алгебраическое дополнение элемента определителя);

3. найти обратную матрицу по формуле:

(3);

4. проверить выполнение условия _{, где Е} — единичная матрица.

№13. Методом союзной матрицы найти А^-1, если .

►1) Найдём detA= – 40;

2) найдём алгебраические дополнения соответствующих элементов матрицы А:

;

Составим союзную матрицу: ;

3) найдём обратную матрицу:

;

4) убедимся, что _{. ◄}

Постановка задачи: найти для квадратной матрицы А обратную, методом элементарных преобразований.

План решения: 1. К данной матрице А приписать справа единичную матрицу ;

2. с помощью элементарных преобразований матрицу А^* привести к виду ;

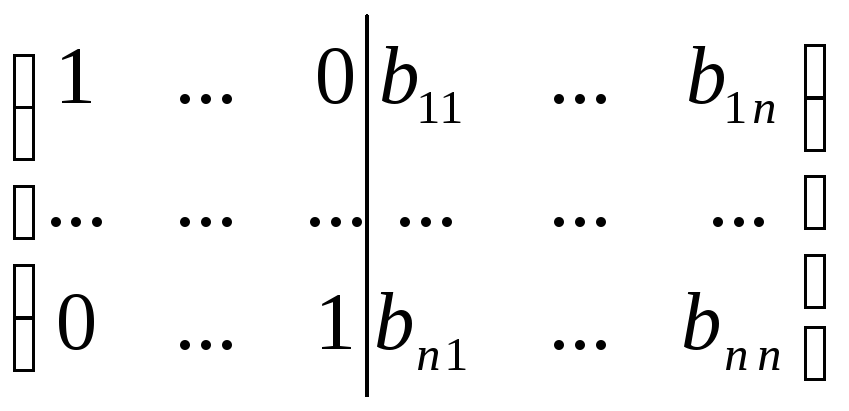3. обратная матрица имеет вид ;

4. проверить выполнение условия _{, где Е} — единичная матрица.

№14. Методом элементарных преобразований найти А^-1 для .

► 1) Образуем матрицу ;

2) В результате последовательных элементарных преобразований получаем:

.

3) обратная матрица имеет вид .

4) проверяем выполнение условия _{, где Е} — единичная матрица. ◄

Постановка задачи: найти ранг матрицы методом элементарных преобразований.

План решения: Так как элементарные преобразования не изменяют ранга матрицы и ранг диагональной (ступенчатой) матрицы равен числу ненулевых строк, то для отыскания ранга матрицы надо:

1. элементарными преобразованиями превратить матрицу в диагональную или ступенчатую;

2. подсчитать число ненулевых строк в получившейся матрице.

№15. Найти ранг матрицы .

► Найдём ранг матрицы методом элементарных преобразований, для этого исходную матрицу с помощью элементарных преобразований сведем к ступенчатой матрице:

.

Полученная ступенчатая матрица содержит две ненулевые строки, значит её ранг равен 2. Следовательно, ранг исходной матрицы также равен 2, т.е. RangB=2. ◄

Постановка задачи: найти ранг матрицы методом окаймления миноров.

План решения: 1. Найти какой-нибудь минор М ¹ первого порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r(A)=0.

2. Вычислить миноры второго порядка, содержащие М ¹ (окаймляющие М ¹) до тех пор, пока не найдётся минор М ² второго порядка, отличный от нуля. Если такого минора нет, то r(A)=1, если есть, то и т.д.

….

k. Вычислять (если они существуют) миноры k-го порядка, окаймляющие минор . Если таких миноров нет, или они все равны нулю, то r(A)=k–1; если есть хотя бы один такой минор , то , и процесс продолжается.

№16. Найти ранг матрицы .

► Найдём ранг матрицы методом окаймляющих миноров. Так как в данной матрице есть ненулевые элементы, то . Так как в данной матрице существует минор второго порядка , то . У данной матрицы минор третьего порядка единственный 0, то . Следовательно, ранг данной матрицы Rang A=2. ◄