
- •Подготовка к части с6 егэ по математике. Содержание.
- •Предисловие.
- •Часть 1. Несколько простых задач для оценки своих сил.
- •Ответы и решения.
- •Часть 2. Разбор типовых задач с6
- •Тема 1. “Число по модулю…”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 2. “Число делится на...”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 3. “Преобразование уравнений”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 4. “Факториалы ”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 5. “Прогрессии ”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 6. “Смешанные задачи”
- •Необходимая теория.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Часть 3. Некоторые советы по подготовке к егэ.
- •Вариант№1
- •Вариант№2
- •Список используемой литературы
Тема 4. “Факториалы ”
Тема не так уж часто встречающаяся в ЕГЭ, но тоже заслуживает рассмотрения.
Необходимая теория.
Факториал числа n — произведение всех натуральных чисел до n включительно:
![]() .
.
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Примеры.
№1
Найдите все тройки натуральных чисел
![]() и
и
![]() ,
удовлетворяющие уравнению
,
удовлетворяющие уравнению
![]()
Решение: Очевидно, что
![]() и
и
![]()
Предположим, что
![]()
Разделим все на
![]()
![]()
Отсюда очевидно, что
![]() ,
то же самое справедливо для
,
то же самое справедливо для
![]() .
.
Далее перебором получаем все возможные результаты.
Ответ:
![]()
№2
Найдите все натуральные значения
![]() ,
для которых выполняется равенство
,
для которых выполняется равенство
![]()
Решение: Представим уравнение в
виде
![]()
Разделим обе части на
![]() и получим
и получим
![]()
Понятно, что
![]() очень мало. Переберем значения начиная
с
очень мало. Переберем значения начиная
с
![]() .
.
![]()
Отсюда видно, что верное решение только
при
![]() .
.
Ответ:
![]()
Номера для самостоятельного решения.
№1
Решите в натуральных числах уравнение
![]()
№2
Уравнение
![]() решите в целых числах
решите в целых числах
№3
Найти наибольшее натуральное число
![]() ,
для которого число
,
для которого число
![]() делится на
делится на
![]() =1,2,…,
=1,2,…,![]()
Ответы и решения.
№1
Ответ:
![]()
№2
Ответ:
![]()
№3
Указание: Рассмотреть случаи при
![]() и при
и при
![]()
Ответ: 46
Тема 5. “Прогрессии ”
Тоже небольшая и редкая тема, но нужно уметь ее решать.
Необходимая теория.
Арифметическая прогрессия — числовая последовательность вида
![]() ,
,
то есть последовательность чисел (членов
прогрессии), каждое из которых, начиная
со второго, получается из предыдущего
добавлением к нему постоянного числа
d (шага или разности прогрессии):
![]()
Любой член прогрессии может быть вычислен
по формуле общего члена:
![]()
![]()
Шаг прогрессии может быть вычислен по
формуле:
![]() ,
если
,
если
![]()
Если шаг d > 0, прогрессия является возрастающей; если d < 0, — убывающей.
Сумма n последовательных членов арифметической прогрессии начиная с члена k:
![]()
Любой член арифметической прогрессии,
начиная со второго, является средним
арифметическим предыдущего и следующего
члена прогрессии:
![]()
![]()
Геометрическая прогрессия —
последовательность чисел
![]() (членов прогрессии), в которой каждое
последующее число, начиная со второго,
получается из предыдущего умножением
его на определённое число (знаменатель
прогрессии), где
(членов прогрессии), в которой каждое
последующее число, начиная со второго,
получается из предыдущего умножением
его на определённое число (знаменатель
прогрессии), где
![]() :
:
![]()
Любой член геометрической прогрессии
может быть вычислен по формуле:
![]()
Если b1 > 0 и q > 1, прогрессия является возрастающей последовательностью, если 0 < q < 1, — убывающей последовательностью, а при q < 0 — знакопеременной
Своё название прогрессия получила по
своему характеристическому свойству:
![]() то есть каждый член равен среднему
геометрическому его соседей.
то есть каждый член равен среднему
геометрическому его соседей.
Сумма n первых членов геометрической
прогрессии:
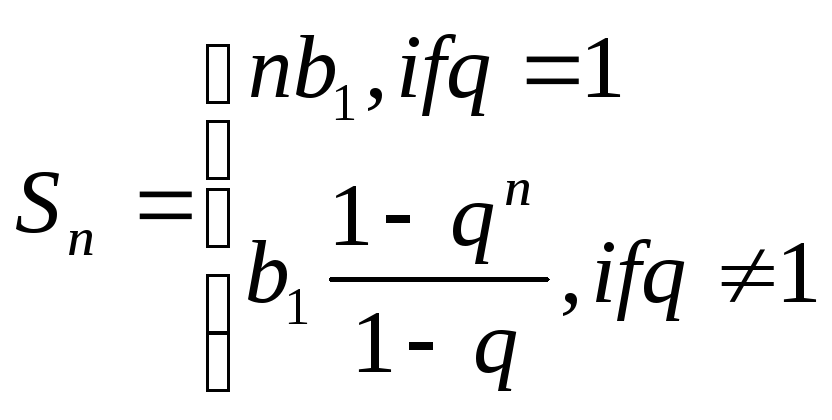
Примеры.
№1
В арифметической прогрессии четвертый
член равен 1. При каком значение
![]() произведение второго и седьмого члена
будет наибольшим?
произведение второго и седьмого члена
будет наибольшим?
Решение:
![]()
Посчитаем производную и найдем максимум
![]()
![]()
Ответ:
![]()
№2
Могут ли числа 2,3 и 17 быть членами (не обязательно последовательными) одной геометрической прогрессии?
Решение: Все 3 числа простые, следовательно, такой геометрической прогрессии не существует.
Ответ: нет
