
- •Подготовка к части с6 егэ по математике. Содержание.
- •Предисловие.
- •Часть 1. Несколько простых задач для оценки своих сил.
- •Ответы и решения.
- •Часть 2. Разбор типовых задач с6
- •Тема 1. “Число по модулю…”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 2. “Число делится на...”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 3. “Преобразование уравнений”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 4. “Факториалы ”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 5. “Прогрессии ”
- •Необходимая теория.
- •Примеры.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Тема 6. “Смешанные задачи”
- •Необходимая теория.
- •Номера для самостоятельного решения.
- •Ответы и решения.
- •Часть 3. Некоторые советы по подготовке к егэ.
- •Вариант№1
- •Вариант№2
- •Список используемой литературы
Тема 3. “Преобразование уравнений”
В этой теме необходимо уметь делать простейшие математические преобразования.
Тема достаточно простая, но требует внимания.
Необходимая теория.
Терема Виета
Если
![]() —
корни многочлена
—
корни многочлена
![]()
(каждый корень взят соответствующее его кратности число раз), то коэффициенты выражаются в виде симметрических многочленов от корней, а именно:
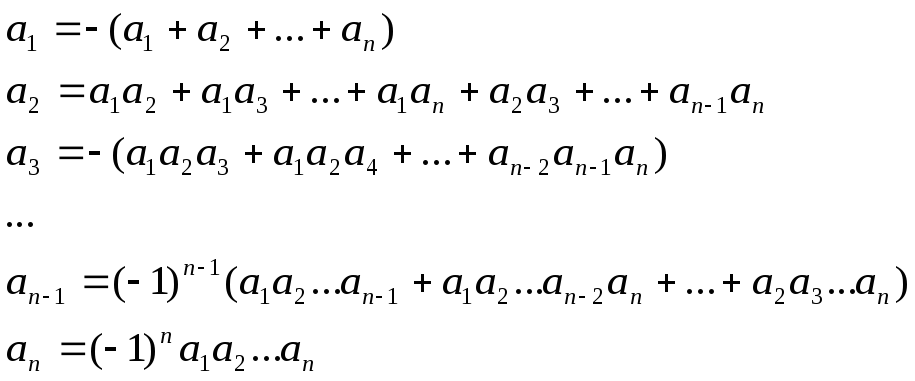
Основные преобразования
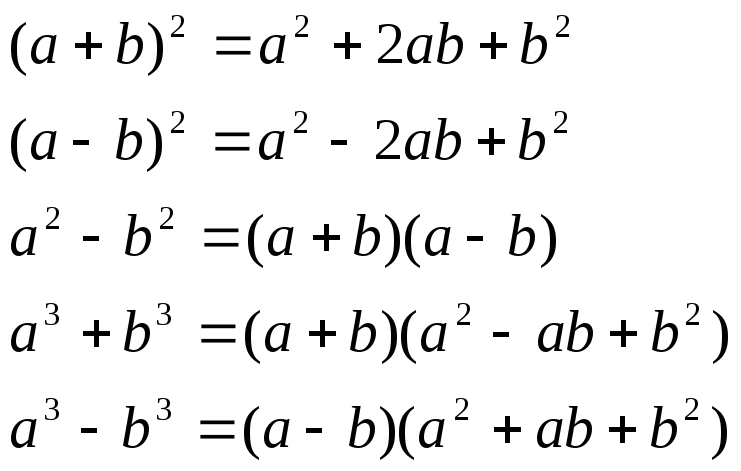
В математике пифагоровой тройкой
называется кортеж из трёх натуральных
чисел
![]() удовлетворяющих
соотношению Пифагора:
удовлетворяющих
соотношению Пифагора:
![]()
Примеры.
№1
Найдите все такие целые
![]() и , что корни уравнения
и , что корни уравнения
![]() являются различными целыми числами, а
коэффициенты
являются различными целыми числами, а
коэффициенты
![]() и
и
![]() - простыми числами.
- простыми числами.
Решение. Пусть![]() и
и
![]() – корни данного уравнения. Тогда, по
теореме Виета:
– корни данного уравнения. Тогда, по
теореме Виета:
![]()
![]()
Так как
![]() - простое, то данная ситуация возможна
или при
- простое, то данная ситуация возможна
или при
![]() ,
или при .
,
или при .
Рассмотрим случай, когда :
![]()
![]() делится на 3. Но
делится на 3. Но
![]() - простое, значит это число делится на
3, а из всех простых чисел, которые делятся
на 3, есть 3
- простое, значит это число делится на
3, а из всех простых чисел, которые делятся
на 3, есть 3![]() – а это число делится на 4, значит оно
не простое, то есть здесь решений нет.
– а это число делится на 4, значит оно
не простое, то есть здесь решений нет.
Осталось рассмотреть случай, когда :
![]()
-![]()
Аналогично рассуждая, как и в первом случае, получаем
![]()
Осталось проверить, что
![]() - простое число:
- простое число:
![]() -
простое.
-
простое.
Ответ: и .
№2
Решите в целых числах уравнение:
![]()
Решение. Данное уравнение сводится к такому:
![]() .
Видим, что данное уравнение представляет
собой пифагоровы тройки, то есть или
.
Видим, что данное уравнение представляет
собой пифагоровы тройки, то есть или
![]() (1)
(1)
![]()
![]()
или
(2)
![]()
![]() .
.
Видим, что в (1) решений нет, так как из
2-го и 3-го равенств получаем, что
![]() .
.
Теперь разберем (2):
Вычитая из 3-го равенство 2-е, получаем:
![]() ,
но из первого равенства видим, что
,
но из первого равенства видим, что
![]() ;
но тогда
;
но тогда![]() ,
а это возможно только в двух случаях:
q=0 или q=1.
При q=0 получаем, что
,
а это возможно только в двух случаях:
q=0 или q=1.
При q=0 получаем, что
![]() при
q=1 получаем, что
при
q=1 получаем, что
![]() ,
но тогда
,
но тогда
![]() -не
целое
-не
целое
Ответ:
Номера для самостоятельного решения.
№1
Решить в целых числах
![]()
№2
Квадратный трехчлен
![]() имеет два различных целых корня. Один
из корней трехчлена и его значение в
точке
имеет два различных целых корня. Один
из корней трехчлена и его значение в
точке
![]() являются простыми числами. Найдите
корни трехчлена.
являются простыми числами. Найдите
корни трехчлена.
№3
Известно что
![]() -
натуральное число. Доказать, что
-
натуральное число. Доказать, что
![]() -
так же натуральное число.
-
так же натуральное число.
№4
Решить уравнение в целых числах
![]()
№5
Решите уравнение
![]() в целых числах
в целых числах
№6
Решить в целых числах систему уравнений
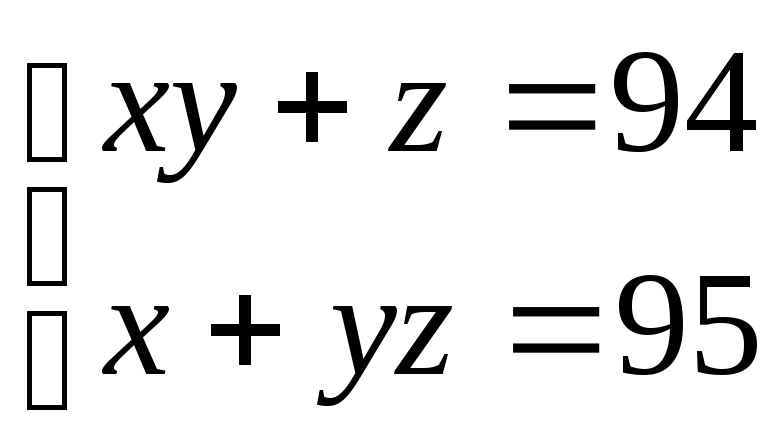
№7
Решите уравнение
![]() в целых числах
в целых числах
№8
Найдите все пары натуральных чисел
разной четности, удовлетворяющие
уравнению
![]()
№9
Решить уравнение
![]() в целых числах
в целых числах
Ответы и решения.
№1
m∙(n-1)(n+1)= 105∙n. Очевидно первое решение n=m=0 и если n и m – решения, то -n и -m – тоже решения.
Если n≠0, то n≠±1 и m≠0. Так как n, (n-1) и (n+1) не делятся на n, то m кратно n, т.е. m = p∙n. Отсюда, p∙(n-1)∙(n+1)= 105 = 25∙55. Числа (n-1) и (n+1) не могут быть нечетными, значит n=2k+1, отсюда p∙k∙(k+1)= 23∙55. Числа k и (k +1) взаимно простые, отсюда следующие решения: k=1, p=12500 и n=3, m=37500 , n=-3, m=-37500, кроме этого случая k и (k+1) могут иметь множители 2 и 5 и так как они разной четности, то, например, k=2j и 2j +1 =5l, причем j<4. Значит j=2, k=4, p=2500 и n=9, m=112500, n=-9, m= -112500.
Ответ:
![]() и
и
![]()
№2
![]() ,
где - простое число. Пусть и
,
где - простое число. Пусть и
![]() - корни, где - тоже простое число. Тогда
по теореме Виета:
- корни, где - тоже простое число. Тогда
по теореме Виета:
![]()
![]()
Получим, что
![]() .
Но, так как
.
Но, так как
![]() -
простое число, то либо
-
простое число, то либо
![]() ,
либо
,
либо
![]() .
Если , то или , что противоречит простоте
числа
.
Если , то или , что противоречит простоте
числа
![]() .
Значит
.
Значит
![]() или
или
![]()
При :
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
что противоречит простоте числа
,
что противоречит простоте числа
![]() .
Следовательно,
.
Следовательно,
![]() .
.
При
![]() :
:![]() . Если
. Если
![]() ,
то
,
то
![]() ,
что противоречит простоте числа .
Следовательно,
,
что противоречит простоте числа .
Следовательно,
![]() , но 9 – не простое число.
, но 9 – не простое число.
Ответ:
![]() и
и
![]() .
.
№3
![]()
![]()
![]()
![]()
![]()
№4
![]()
![]()
![]()
![]()
![]()
![]()
![]()
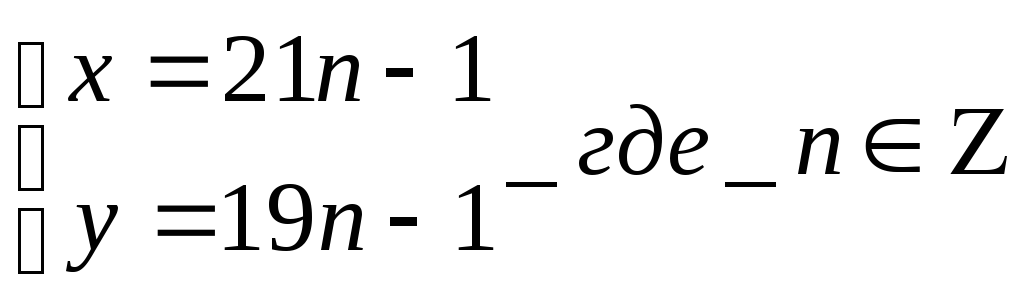
Ответ:
![]()
№5
Вынесем общий множитель за скобку
![]()
Рассмотрим все возможные ситуации
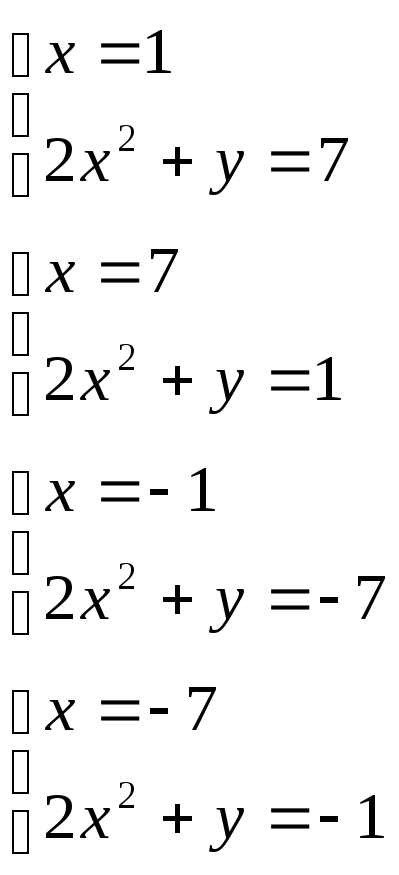
Ответ:
![]()
№6
Вычтем из первого уравнения второе
![]()
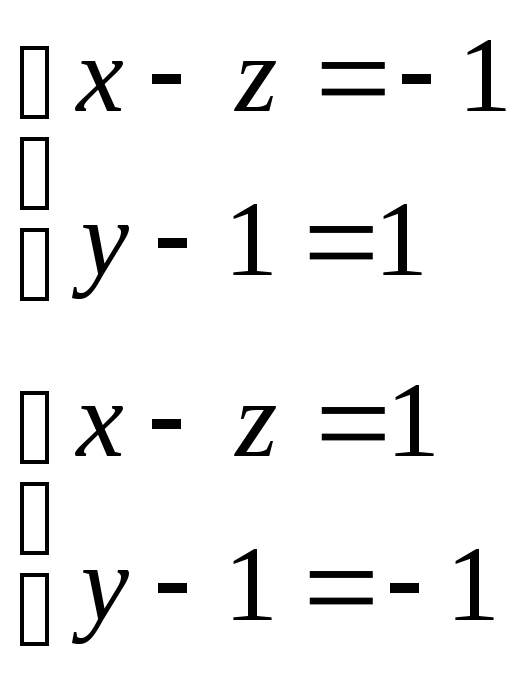
Ответ:
![]()
№7
Ответ:
![]()
№8
Указание: Представить уравнение в
виде
![]() ,
где
,
где
![]() -нечетно,
а
-нечетно,
а
![]() -четно.
Рассмотреть все варианты с
-четно.
Рассмотреть все варианты с
![]() и
и
![]()
Ответ:
![]()
№9
Указание: Представим как разность
кубов
![]() и рассмотрим все возможные варианты.
и рассмотрим все возможные варианты.
Ответ:
![]()
