4.6. Границя функції. Нескінченно малі та нескінченно великі функції

Означення. Нехай функція f(x) визначена в деякому проколеному околі точки x₀. Число a називається границею функції f(x) у точці x₀, якщо для будь-якого додатного числа існує таке додатне число (залежне від ), що для всіх значень x із проколеного –околу точки x₀ відповідні значення f(x) належать до –околу точки a (див. рис. 4.2). Це можна коротко записати так:

,

або .

Рис. 4.2.

Зауваження. Згідно з означенням у самій точці x₀ функція f(x) може бути не визначена.

Те, що функція f(x) має в точці x₀ границю a ,позначається так:

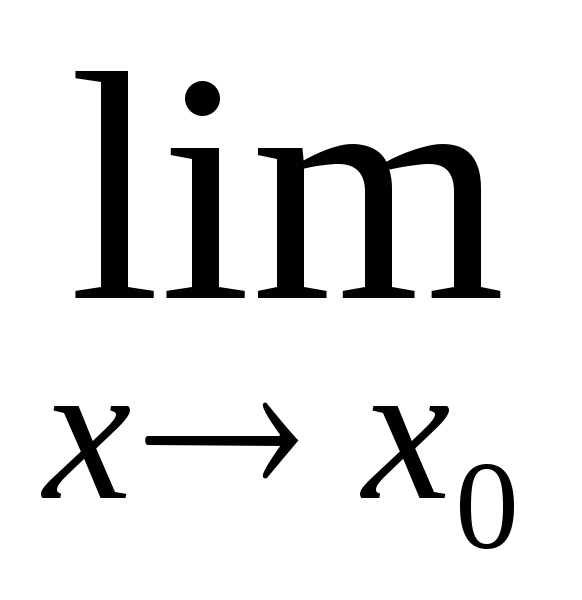f(x) = a.

Читається: границя f(x) в точці x₀ дорівнює a. Позначення походить від латинського limes (границя). Іноді пишуть також:

f(x)  a при x  x₀

(f(x) прямує до границі a при x, що прямує до x₀).

Означення. Нехай функція f(x) визначена при всіх х, що задовольняють нерівність |x| > K при K > 0. Число a називається границею функції f(x) на нескінченності, якщо для будь-якого існує таке число (залежне від ), що |f(x) – a|< для всіх значень x, які задовольняють нерівність |x| > M. Коротко це записують так:

.

В цьому разі пишуть: f(x) = a або f(x)  a при x .

Іноді виникає потреба розглядати лише додатні або лише від’ємні значення x. Для цього запровадимо односторонні границі функції на нескінченності, а саме

Означення. Нехай функція f(x) визначена при всіх х, що задовольняють нерівність x > K (x < – K) при K > 0. Число a називається границею функції f(x) на плюс нескінченності (мінус нескінченності), якщо для будь-якого існує таке число (залежне від ), що |f(x) – a|< для всіх значень x, які задовольняють нерівність x > M (x < – M).

В цьому разі пишуть: f(x) = a (f(x) = a).

Означення. Функція f(x) називається нескінченно малою в точці x₀, якщо 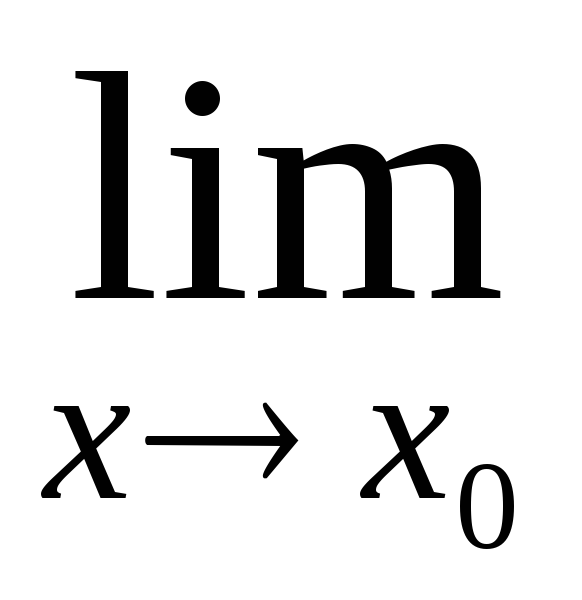f(x) = 0.

Теорема (про зв'язок нескінченно малих з границею). Для того, щоб 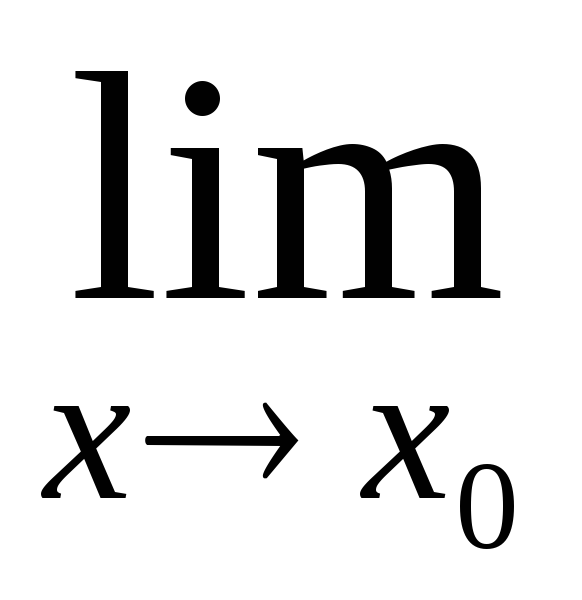f(x) = a, необхідно і достатньо, щоб функція g(x) = f(x) – a була нескінченно малою в точці x₀ (тобто щоб функція f(x) була зображувана у вигляді f(x) = g(x) + a , де g(x) нескінченно мала в точці x₀).

Необхідність. Дано, що 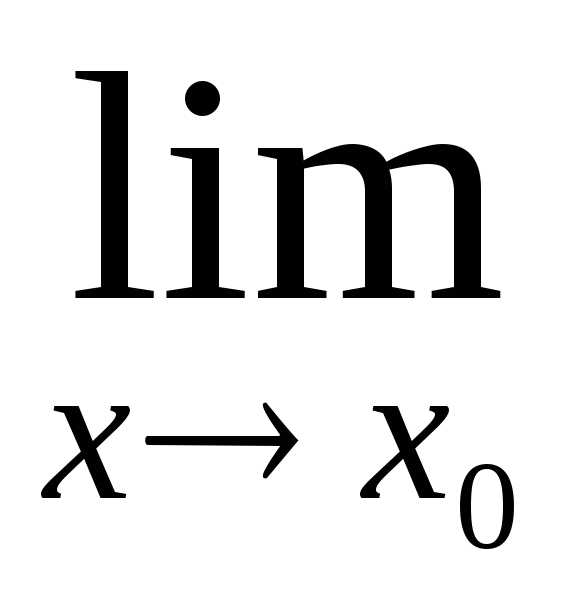f(x) = a. Тоді для будь-якого числа існує таке число , що для всіх значень x, для яких виконується нерівність | x – x₀| < , виконується також нерівність |f(x) – a| <  . Оскільки g(x) = f(x) – a, то останню нерівність можна записати як |g(x)| = |g(x) – 0| < , а це і означає, що 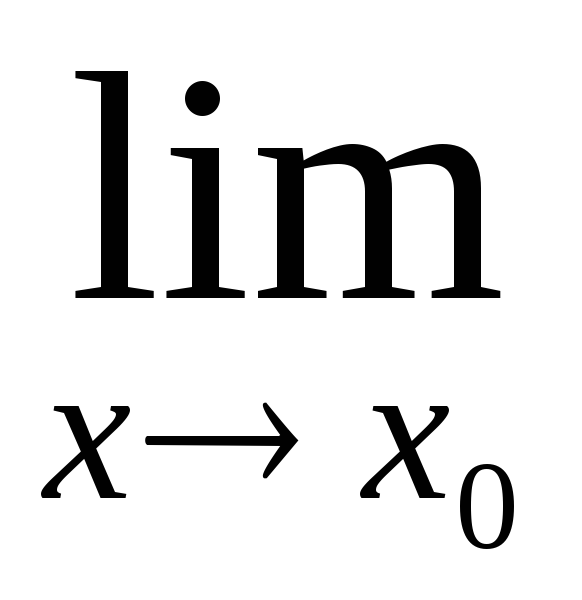g(x) = 0.

Достатність. Дано, що f(x) = g(x) + a, де g(x) нескінченно мала в точці x₀. Тоді для будь-якого числа існує таке число , що для всіх значень x, для яких виконується нерівність | x – x₀| < , виконується також нерівність |g(x)| = |f(x) – a| < , а це означає, що f(x) = a.

Теорема (про добуток нескінченно малої функції на обмежену). Якщо функція u(x) обмежена в деякому околі , а функція g(x) – нескінченно мала в точці x₀, то функція f(x) = u(x)g(x) нескінченно мала в точці x₀.

Доведення. Обмеженість u(x) означає, що знайдеться таке число М, що для всіх |u(x)|  M.

Функція g(x) нескінченно мала в точці x₀, тобт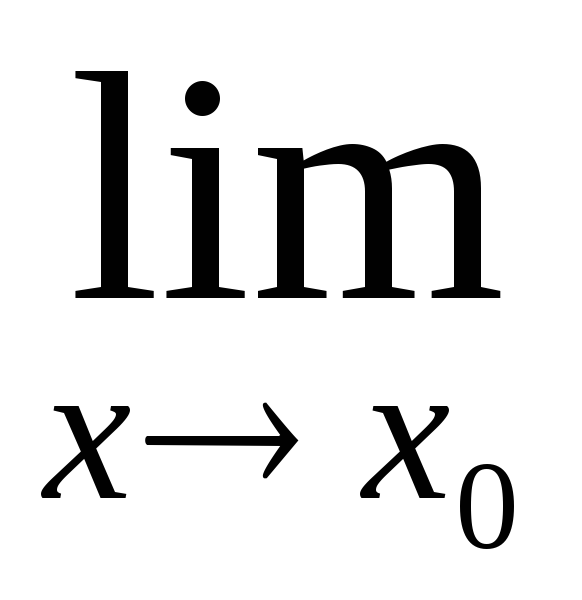о f(x) = 0. Це означає, що . Нехай - переріз множин та . Тоді для заданого , а це означає, що f(x) = 0, тобто f(x) = u(x)g(x) нескінченно мала в точці x₀.

Приклад. Функція f(x) = нескінченно мала в точці х = 0, бо 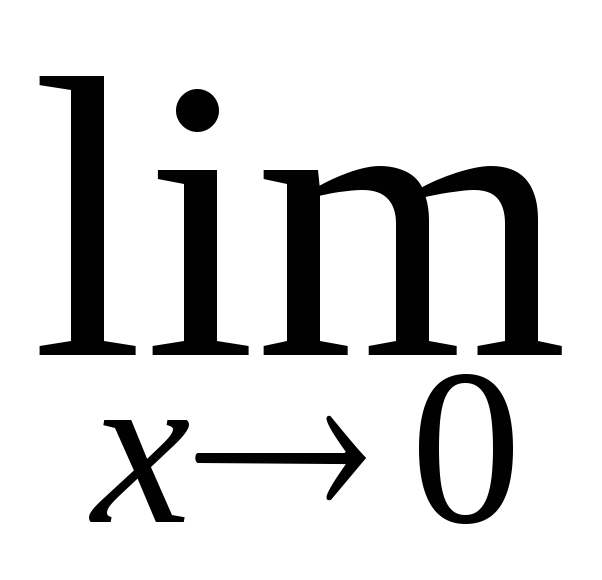x = 0, а для всіх х ≠ 0, тобто це обмежена функція.

Означення. Функція f(x) називається нескінченно великою в точці x₀, якщо для будь-якого числа М існує таке додатне число (залежне від М), що для всіх значень x із проколеного –околу точки x₀ вірна нерівність |f(x)| > M, або коротко .

Це записується так:

f(x) = .

При цьому слід мати на увазі, що нескінченно велика функція границі не має (символ  не є числом).

Теорема (про зв'язок між нескінченно малими і нескінченно великими функціями). Якщо функція f(x) нескінченно мала в точці x₀, то функція нескінченно велика в цій точці, і навпаки.

Доведення.

Функція f(x) нескінченно мала в точці x₀, тобт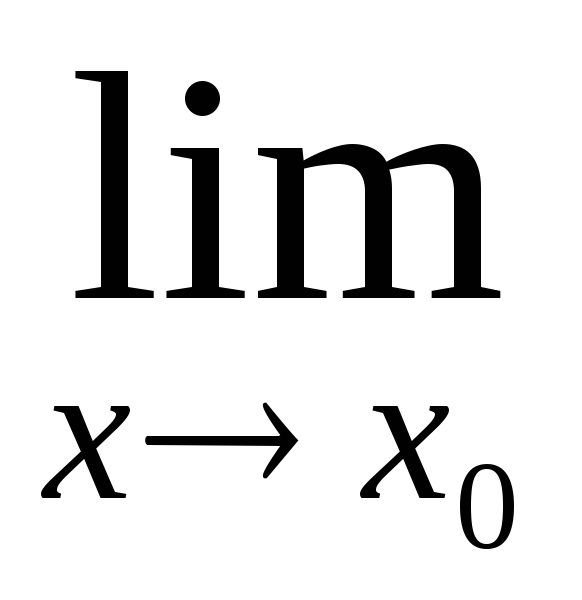о f(x) = 0. Це означає, що . Тоді для заданого M , а це означає, що функція нескінченно велика в точці x₀.

Зауваження. Означення нескінченно малих і нескінченно великих функцій і теореми, що з них випливають, залишаються в силі і для границь на нескінченності.

Приклад 1. Функція f(x) = 2х – 6 нескінченно мала в точці x₀ = 3, отже функція g(x) = нескінченно велика в цій точці.

Приклад 2. Функція f(x) = х + 4 нескінченно велика при x  , отже функція g(x) = нескінченно мала при x  .