Решение

Тор представляет собой поверхнсть вращения окружности радиуса R = (R₂ - R₁)/2 вокруг оси, расположенной вне окружности. Полагая провод тонким по сравнению с радиусом тора, можно считать, что линии тока лежат в меридианальных плоскостях, т.е. в плоскостях, проходящих через ось вращения. При этом предположении при повороте тора с намотанным на него проводом с током вокруг оси он совмещается сам с собою. То же относится и к силовым линиям индукции магнитного поля тока. Поэтому силовые линии поля представляют собой концентрические окружности с центрами на оси вращения. Циркуляция вектора индукции магнитного поля вдоль каждой такой окружности радиуса r равна 2rB(r) Полный ток, пронизывающий площадь, ограниченную этой окружностью, равен NI, если окружностьпроходит внутри тора, и равен нулю, если она проходит вне тора. Таким образом, индукция поля отлична от нуля только внутри тора, т.е при R₁ <r< R₂ и составляет . Величина n=NI/2r представляет собой число витков, приходящееся на единицу длины обмотки. Величина i=nI представляет собой линейную плотность тока.

21. Соленоид представляет собой полый цилиндр радиуса R и длины L, на поверхность которого плотно намотан в один слой тонкий провод. Отношение числа витков провода в обмотке соленоида к его длине составляет n. Определить индукцию магнитного поля внутри и вне соленоида, если по его обмотке течет ток I. Провести оценки для следующих величин: R=1 см, L=50 см, n=15 витков/см, I=1 А.

Решение

Соленоид можно представить себе как предельный случай тора очень большого радиуса вращения, но фиксированного радиуса цилиндра R при увеличении числа витков обмотки, но фиксированном отношении n числа витков к длине окружности вращения. Индукция магнитного поля внутри соленоида составляет B= ₀nI, вне соленоида B=0.

Давление магнитного поля p=B²/2₀. Сила давления, действующая на боковую поверхность соленоида, площадь которой S=2RL составит

F=pS=₀(nI)²S/2=₀(nI)²RL

Численные оценки:

B=1.256 10^-6 15 1=1.88 10^-5 Тл p=1.41 10^-4Н/м² F=4.44 10^-6 Н

Магнитное поле в веществе. Теорема о циркуляции для магнитного поля в веществе. Граничные условия на поверхностях раздела сред.

В веществе происходит движение заряженных частиц внутри атомов и молекул, т.е. кроме токов проводимости существуют внутренние токи. Внутренние токи также являются источниками магнитного поля. Каждый такой ток замкнут внутри микрочастиц и обладает магнитным моментом. Под действием внешнего магнитного поля эти магнитные моменты, а с ними и все вещество приобретает магнитный момент, пропорциональный числу микрочастиц, а следовательно и объему вещества. Отношение магнитного момента вещества к его объему называют вектором намагниченности . При однородной намагниченности в объеме вещества внутренние токи в среднем компенсируют друг друга. Некомпенсированными остаются только токи, выходящие на боковую поверхность тела. Эти токи в среднем складываются в поверхностный ток I_m , который и является источником намагниченности вещества. Магнитный момент этого тока составляет I_mS=JSl, где l – длина боковой поверхности тела. Отсюда получается J=I_m/l=i_m, т.е. намагниченность равна поверхностному току, приходящемуся на единицу длины поверхности, или линейной плотности поверхностного тока. Следует при этом иметь в виду, что поверхностный ток, порождающий намагниченность, может протекать как по реальной поверхности, так и по мысленно выделяемой. Последнее обстоятельство позволяет определить циркуляцию вектора намагниченности. Пусть в пространстве проведен произвольный замкнутый контур L. Предположим, что этот контур окружен тонкой трубкой. В магнетике по ее поверхности протекает поверхностный ток с линейной плотностью i_m, протекающий в плоскости, перпедикулярной Магнитный момент этого тока направлен вдоль перпендикуляра к плоскости, в которой течет поверхностный ток, т.е. вдоль касательной к контуру. Линейная плотность этого тока определяет проекцию J_l намагниченности на направление касательной к контуру. Полный внутренний ток, пронизывающий поверхность, опирающуюся на контур L, будет

С учетом последнего равенства теорему о циркуляции для вектора индукции можно переписать в виде

Отсюда видно, что для вектора циркуляция определяется только током проводимости, пронизывающим контур, т.е.

В этом состоит смысл введения вектора . Вектор называют напряженностью магнитного поля.

Векторы индукции и намагниченности зависят от напряженности магнитного поля. В общем случае эти функциональные зависимости неизвестны. Однако в слабых полях эти зависимости линейны, т.е. , . Величины  и =1+ называются магнитной восприимчивостью и относительной магнитной проницаемостью вещества соответственно.

Так же как и для электрического поля, из теоремы Гаусса для индукции магнитного поля следует непрерывность нормальных проекций вектора индукции на границе раздела различных сред. Из теоремы о циркуляции следует непрерывность касательных проекций напряженности магнитного поля, если по границе раздела не протекают поверхностные токи проводимости. Таким образом, граничные условия имеют вид:

B_n1= B_n2 H_t1= H_t2

22. Вблизи точки А на границе магнетик-вакуум магнитная индукция в вакууме равна 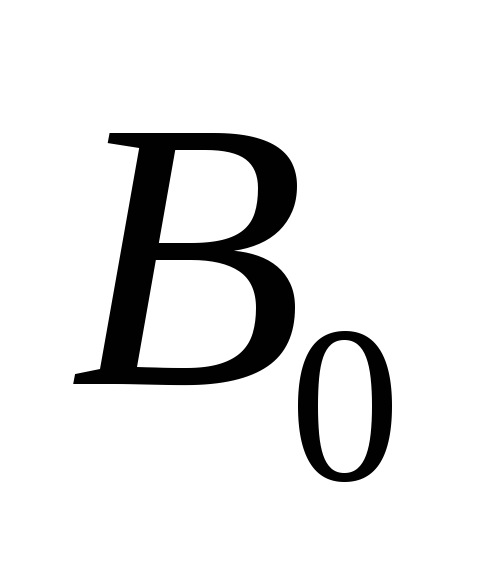, причем вектор индукции составляет угол  с нормалью к поверхности раздела в данной точке. Магнитная проницаемость магнетика составляет . Определить вектор индукции в магнетике вблизи точки А.