Пользуясь тригономерическим тождеством

,

получим . Подставив числа, получим β≈74˚, Е₁=5.2 В/м

10. Плоский конденсатор с площадью пластин S и расстоянием между ними d подключен к батарее с разностью потенциалов U. Параллельно обкладкам в него вдвигают проводящую пластину толщины L<d. Определить напряженность электрического поля во всем пространстве между обкладками конденсатора и емкость образовавшейся системы.

Решение.

Конденсатор с вдвинутой в него проводящей пластиной можно рассматривать как два последовательно соединенных плоских конденсатора с расстоянием между пластинами d₁ и d₂, причем d₁₊ d₂=d-L. Емкости этих конденсаторов C_1,2=ε₀S/d_1,2. При последовательном соединении складываются обратные величины емкостей:

,

Заряд на пластинах конденсатора q=CU, напряженность поля в воздухе между пластинами E=q/ε₀S=U/(d-L), внутри металлической пластины Е=0.

11. Плоский конденсатор с площадью пластин S и расстоянием между ними d подключен к батарее с разностью потенциалов U. Параллельно обкладкам в него вдвигают диэлектрическую пластину толщины L<d с диэлектрической проницаемостью ε. Определить напряженность электрического поля во всем пространстве между обкладками конденсатора и поверхностную плотность поляризационных зарядов.

Решение.

Индукция и напряженность электричекого поля в плоском конденсаторе перпендикулярны пластинам конденсатора и плоскости диэлектрической пластины, т.е. имеет только нормальную составляющую. Следовательно, индукция поля в конденсаторе непрерывна.

В воздушных промежутках напряженность поля E=q/ε₀S, индукция D= ε₀E=q/S. В диэлектрике напряженность поля E₁, индукция D= εε₀E₁=q/S. Таким образом, E₁=q/εε₀S=E/ε, разность потенциалов между пластинами конденсатора:

U=E(d-L)+ E₁L=E(d-L+L/ε)=q(d-L+L/ε)/ε₀S,

q=Uε₀S/(d-L+L/ε)

E=U/(d-L+L/ε), E₁= E/ε= U/ε(d-L+L/ε)

Поляризация диэлектрика P=D- ε₀ E₁=(ε-1)ε₀E₁=(ε-1)ε₀ U/ε(d-L+L/ε) равна поверхностной плотности поляризационных зарядов σ_пол= -Р=-(ε-1)ε₀ U/ε(d-L+L/ε)

12. Сферический конденсатор образован двумя концентрическими проводящими сферами радиусов R₁ и R₂ (R₁ < R₂). Внутренней сфере сообщают заряд q, а внешней –q. Определить разность потенциалов между обкладками сферического конденсатора, его емкость и энергию электрического поля.

Решение

Напряженность поля в сферическом конденсаторе: E(r )=kq/r², если R₁<r< R₂. Разность потенциалов между пластинами

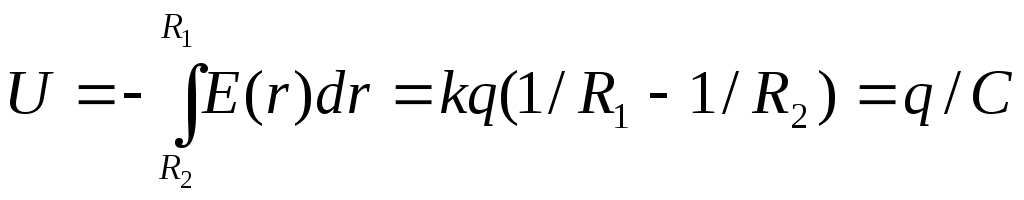
Отсюда находим емкость конденсатора C=4πε₀/(1/R₁-1/R₂). Энергия поля составляет

W_эл=q²/2C

Постоянный электрический ток. Закон Ома для участка элекрической цепи и для замкнутой цепи. Закон Джоуля – Ленца. Правила Кирхгофа.

При протекании электрического тока заряды, переносящие ток, не исчезают и не появляются, т.е. имеет место закон сохранения электрическог заряда. Плотностью электрического тока называют вектор, направление которого совпадает с направлением движения положительных зарядов. Если - внешняя нормаль к площадке dS, и через нее за время dt проходит заряд dq, то проекция вектора плотности тока на направление нормали составит

Если плотность электрического заряда ρ, то полный заряд Q внутри замкнутой поверхности S, ограничивающей объем V, будет

Заряд внутри поверхности изменяется только вследствие втекания электрического тока внутрь поверхности S, т.е.

Это уравнение выражает закон сохранения электрического заряда при протекании электрического тока.

Опыт показывает, что вектор плотности тока направлен по направлению вектора напряженности электрического поля и пропорционален его величине, т.е.

Здесь  - удельная проводимость,  - удельное сопротивление среды. Это закон Ома в дифференциальной форме.

Если dS и dl – площадь и толщина слоя среды объемом dV=dSdl, перпендиулярного направлению плотности тока, то разность потенциалов в этом слое составит d=Edl. За время dt через этот слой пройдет заряд dq=jdSdt, при этом на перемещение этого заряда затрачивается работа dA=dq d=jEdVdt. Эта работа выделяется в виде тепла dQ=dA. Таким образом, плотность тепловой мощности dQ/dVdt=w при протекании тока составляет

Это закон Джоуля-Ленца в дифференциальной форме.

В случае длинных тонких проводников плотность тока можно выразить через полный ток I, протекающий через проводник площадью поперечного сечения S: j=I/S=E/.Тогда разность потенциалов на концах этого проводника длиной l составит U==El= Il/S=IR. Окончательно получаем закон Ома для участка электрической цепи в интегральной форме

U=IR , R=l/S

Величина R называется электрическим сопротивлением участка цепи.

При последовательном соединении проводников ток в цепи один и тот же, а падение напряжений на отдельных участках цепи складывается. Поэтому при последовательном соединении

R= R_i , R_i - сопротивление i –го проводника.

При параллельном соединении полный падение напряжения на всех проводниках одинаково, а токи в отдельных проводниках I_i складываются, I= I_i, т.е. U/R= U (1/R_i). Таким образом, при параллельном соединении проводников складываются обратные величины сопротивлений

Мощность тока, выделяющаяся на сопротивлении R составляет

W=IU=I²R=U²/R

Это закон Джоуля-Ленца в интегральной форме.

Протекание стационарного тока в электрической цепи возможно только в замкнутой цепи при условии, что в цепи есть источники тока, т.е. такие устойства, в которых производится разделение электрических зарядов за счет работы неэлектрических, т.е. сторонних сил. Отношение работы таких сил к величине заряда, полученного в результате этой работы, называют электродвижущей силой (ЭДС) Є источника тока. Кроме того, источники тока характеризуются величиной внутреннего сопротивления r. Тогда теорема о циркуляции для электрическог поля в замкнутой цепи будет иметь вид:

I  R_k+Ir_i+ Є_i=0,

причем величины ЭДС считаются положительными, если при выбранном направлении обхода контура (которое в данном случае совпадает с положительным направление тока) источник ЭДС проходится от положительного полюса к отрицательному. Это закон Ома для замкнутой цепи.

При расчете сложных электрических цепей следует пользоваться правилами Кирхгофа. Для этого в цепи нужно выделить замкнутые контура, и объединить все участки контуров, которые принадлежат только одному контуру. В таких объединенных участках нужно выделить параллельные и последовательные соединения и найти их сопротивления по приведенным выше правилам для параллельных и последовательных соединений. Далее, в каждом таком участке цепи задаться величиной I_i и положительным направлением тока. Для разветвлений цепи записать закон сохранения электрического заряда:

 I_i=0

В этих уравнениях неизвестные токи следует брать со знаком + , если ток входит в разветвление, или со знаком - , если выходит из разветвления. Это первое правило Кирхгофа.

Далее, в выделенных ранее контурах задаться направлениями обхода и записать закон Ома для каждого из участков, принадлежащих только одному контуру, считая падение напряжения положительным, ес ли направление обхода контура в этом участке совпадает с выбранным ранее положительным направлением тока. В противном случае падение напражения следует считать отрицательным. Затем для каждого из контуров записать теорему о циркуляции, руководствуясь приведенным выше правилом для выбора знаков ЭДС и учитывая внутренние сопротивления источников тока. Это второе правило Кирхгофа. Получившаяся система уравнений для токов является линейной. Ее всегда можно решить, используя любой из известных из математики способов. При этом число уравнений может быть больше, чем неизвестных. Тогда известными из математики способами следует выделить только независимые, т.е. не являющиеся следствием остальных уравнения. Руководствуясь правилами Кирхгофа, можно произвести расчет любой сложной цепи.

Задачи.

13. Электрическая цепь состоит из источника тока с постоянной ЭДС Є и внутренним сопротивлением r и внешнего сопротивленя R. Определить, как зависит полезная мощность, выделяемая на внешнем сопротивлении, и КПД источника в цепи от величины внешнего сопротивления R. Построить графики этих зависимостей. При какой величине сопротивленя R тепловая мощность, выделяемая в нем, будет максимальна?

Решение.

Для нахождения тока следует воспользоваться законом Ома для замкнутой цепи

IR+Ir-Є=0.

Отсюда получается ток I=Є/(R+r). Мощность, выделяющуюся в сопротивлении, следует найти по закону Джоуля-Ленца:

W_R=I²R=Є²R/(R+r)²

Мощность, расходуемая источником тока:

W_Є=ЄI=Є²/(R+r)

Тогда КПД составит:

КПД= W_R/ W_Є =R/(R+r)

Для нахождения максимальной мощности, выделяющейся в сопротивлении, используем условие максимума функции:

dW_R/dR=Є²[((R+r)²-2R(R+r)]/ (R+r)⁴=Є²(r-R)/(R+r)³=0,

т.е. максимальная мощность выделяется в сопротивлении при R=r и составляет

(W_R)_макс=Є²/4r

14. В электрической цепи определить показания идеальных вольтметра и амперметра. ЭДС источников тока и их внутренние сопротивления равны соответственно: Є₁=9 В, Є₂= 12В, r₁=3 Ом , r₂=4 Ом, сопротивление резистора R=5 Ом. Какое количество тепла выделится в резисторе R за время t=10 с?

Решение.

Идеальный вольтметр обладает бесконечным внутренним сопротивленим, идеальный амперметр – нулевым внутренним сопротивленим. По закону Джоуля-Ленца в резисторе R за время t выделится энергия Q=I²Rt. Таким образом, требуется найти ток через резистор R.

I

I₁

I₂

Є₁

Є₂₂

R

r₁

r₂

По первому правилу Кирхгофа имеем:

I₁+I₂=I

Выберем направление обхода контуров по часовой стрелке. Для контуров, содержащих резистор R и источники тока по второму правилу Кирхгофа имеем:

IR+I₁r₁ - Є₁=0

-IR - I₂r₂ - Є₂=0

Выражая из первого уравнения ток I₂ и подставляя в последнее уравнение, имеем:

IR+I₁r₁ =Є₁

IR +Ir₂ - I₁ r₂=-Є₂

Умножая первое уравнение на r₁, а второе – на r₂ и складывая, получим

I=( r₂Є₁ - r₁Є₂)/(R(r₁+r₂)+r₁r₂)

Окончательно, Q=I²Rt. Подставляя численные значения, получим I=0, Q=0.

15. Определить заряд конденсатора в цепи в установившемся режиме. Считать все параметры элементов цепи известными. Какое колическво теплоты выделится на резисторах R₁ и R₂ после размыкания ключа?

Решение.

В установившемся режиме ток через конденсатор не течет, он заряжен до напряжения, равного падению напряжения на резисторе R₂. Полное сопротивление замкнутого контура, по которому протекает ток, образовано последовательно соединенными сопротивлениями резисторов R₂ и R₃ и внутренним сопротивлением источника тока. По закону Ома для замкнутой цепи ток в ней составит

I=Є/(R₂ + R₃+r)

Падение напряжения на резисторе R₂

U=I R₂=Є R₂/(R₂ + R₃+r)

Электрическая энергия, запасенная в конденсаторе, после замыкания ключа перейдет в теплоту Q, которая выделится на резисторах R₁ и R₂ ,

Q=CU²/2

Магнитное поле. Сила Лоренца, сила Ампера.

В опытах Ампера было установлено, что на проводник с током в магнитном поле действует сила, пропорциональная величине тока I, длине проводника l, величине индукции магнитного поля B и синусу угла α между направлениями тока и вектора индукции магнитного поля. Эту силу называют силой Ампера.

F=IlBsinα.

В системе единиц СИ коэффициент пропорциональности равен единице, а закон Ампера используют для определения единицы индукции магнитного поля: за единицу индукции 1 Тл (Тесла) принимают такую ее величину, при которой на проводник длиной 1 м с протекающим по нему током силой 1 А, направленным перпендикулярно направлению поля действует сила 1 Н. Линия действия силы Ампера перпендикулярна плоскости, в которой лежат векторы и . Направление вектора силы определяется правилом правого винта: если правый винт вращать в сторону меньшего угла от к , то направление движения винта укажет направление вектора .

В математике векторным произведением называют вектор, по абсолютной величине равный c=absinα, α – угол между векторами и , перпендикулярный плоскости, в которой лежат векторы и . Направление вектора определяется правилом правого винта: если правый винт вращать в сторону меньшего угла от к , то направление движения винта укажет направление вектора .

Если вектор направить по направлению тока, то с помощью векторного произведения силу Ампера можно представить в векторном виде

.

Опыт показывает, что на движущийся в магнитном поле электрический заряд действует сила, пропорциональная величине заряда q, его скорости v, величине индукции магнитного поля B и синусу угла α между направлениями вектора скорости заряда и вектора индукции магнитного поля. Эту силу называют силой Лоренца. В системе единиц СИ коэффициент пропорциональности равен единице. В векторной форме сила Лоренца есть

.

Задача Д1.

В масс-спектрометре заряженные частицы массой m и зарядом q первоначально ускоряются в электрическом поле, проходя без начальной скорости разность потенциалов U. Затем они поступают в магнитное поле с индукцией B перпендикулярно направлению поля и движутся в магнитном поле по окружности радиуса R. Определить удельный заряд частиц q/m.

Решение.

При ускорении заряженной частицы в электрическом поле потенциальная энергия частицы, при прохождении разности потенциалов U составляющая qU, переходит в кинетическую энергию:

При попадании частицы в магнитное поле перпендикулярно направлению поля частица под действием силы Лоренца движется по дуге окружности радиуса R:

Отсюда получается vBR=2U, или v=2U/RB. С другой стороны, из второго уравнения следует v=(q/m)RB, и окончательно

(q/m)=2U/(RB)² .

Задача Д2.

Плоская прямоугольная катушка из N=100 витков со сторонами a=10 см и b=20 см находится в однородном магнитном поле с индукцией В=0.1 Тл. Каков максимальный вращающий момент может действовать на катушку, если сила тока в катушке I=2A.

Решение.

Пусть ось x направлена вдоль одной из сторон катушки, ось y – вдоль другой стороны, ось z - параллельно нормали к плоскости катушки, начало координат выбрано в одной из вершин катушки. При вращении правого винта по направлению тока в катушке винт движется в

y

I

1

2

b

0

x

a

3

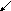
z

направлении единичного вектора нормали . На рисунке показаны положение и размеры

катушки и направление тока I. В выбранной системе координат вектор нормали совпадает с базовым вектором системы координат. Токи в проводниках 03 и 12 противоположны по направлению, а длины этих проводников равны. Поэтому силы Ампера, действующие на эти проводники, равны и противоположны, т.е. образуют пары сил. Момент пары этих сил составляет . Аналогично, момент пары сил, действующих на проводники 01 и 23 составляет . Для сил Ампера имеем , . Подставляя выражения для сил Ампера в выражения для моментов и раскрывая по правилам двойные векторные произведения, для полного момента сил, действующих на виток катушки, получается следующее выражение

Замечая, что векторное произведение , полный момент сил Ампера, действущих на виток катушки, можно представить в виде

,

где S=ab – площадь витка. Можно определить магнитный момент витка с током как , вектор нормали к плоскости витка образует правовинтовую систему с направлением тока в витке. Тогда момент сил Ампера составит . Последние два выражения записаны в инвариантой виде, т.е. не зависят от выбора системы координат и применимы для витков любой формы.

Складывая моменты сил, действующих на каждый виток катушки, получаем полный момент сил

,

Он максимален, когда вектор индукции перпендикулярен нормали к плоскости витков катушки и составляет M_макс=NISB. Подставляя численные значения, находим

M_макс=100 2 0.1 0.2 0.1=0.4 Н м

Закон Био-Савара. Теорема о циркуляции для магнитного поля.

Источником магнитного поля являются движущиеся заряды и токи. Опыт показывает, что индукция магнитного поля заряда q, движущегося со скоростью , пропорциональна величине заряда, его скорости и обратно пропорциональна квадрату расстояния от заряда до точки наблюдения r. Вектор индукции перпендикулярен плоскости, в которой лежат вектор скорости и вектор , проведенный из места нахождения заряда в точку наблюдения. Направление вектора индукции определяется направлением движения правого винта при его вращении от вектора скорости к радиусу-вектору точки. В системе единиц СИ коэффициент пропорциональности составляет ₀=1.256 10^-6 Гн/м.

Опыт показывает также, что для магнитного поля имеет место принцип суперпозиции: магнитое поле многих движущихся зарядов равно векторной сумме полей, создаваемых каждым из зарядов по отдельности. Если плотность движущихся со скоростью зарядов в малой окрестности пространства объемом dV составляет n, то число их составляет dN=ndV. Так как плотность тока есть , то в соответствии с принципом суперпозиции вклад в индукцию этих зарядов будет

Это закон Био-Савара в дифференциальной форме. Если ток I проходит по длинному тонкому проводнику, то , где - вектор отрезка проводника длиной dl в направлении тока. Тогда закон Био-Савара можно представить в интегральной форме:

Так как ток всегда протекает по замкнутому контуру L, то полное поле тока будет

В математике доказывают теорему о циркуляции вектора индукции магнитного поля. Она формулируется следующим образом. Пусть в пространстве имеется произвольная замкнутая кривая – замкнутый контур L. Пусть также на этот контур опирается произвольная поверхность S. В каждой точке контура L можно провести касательную и определить проекцию B_l вектора магнитной индукции на направление касательной и дифференциал длины дуги кривой dl. В каждой точке поверхности можно провести нормаль к поверхности и определить проекцию вектора плотности тока j_n на направление нормали и дифференциал площади поверхности dS. Как следствие закона Био-Савара между векторами индукции магнитного поля и плотности тока имеет место интегральная связь:

которая представляет собой теорему о циркуляции в интегральной форме. Здесь I – полный ток, пронизывающий замкнутый контур.

В общем случае теоремы о циркуляции недостаточно, чтобы определить вектор индукции магнитного поля. Если магнитное поле по условиям задачи обладает высокой симметрией, то теорему о циркуляции можно использовать для определения поля.

Для магнитного поля имеет место теорема Гаусса. Так как магнитных зарядов не существует, то теорема Гаусса имеет простой вид. Для произвольной замкнутой поверхности S поток вектора магнитной индукции равен нулю:

16. По круговоаму витку радиуса R циркулирует ток I. Определить индукцию магнитного поля на оси витка в зависимости от расстояния х от его центра. Построить график этой зависимости. Исследовать предельные случаи x<<R и x>>R.