3.5.3. Вычисление изменения энтропии идеального газа.

Для обратимого процесса простой системы справедливо:

, а ,

поэтому

(3.31)

(фундаментальное уравнение термодинамики).

Объединенное уравнение первого и второго законов термодинамики (3.31) для равновесных процессов можно записать как

.

Для идеального газа фундаментальное уравнение принимает вид

,

. (3.32)

После интегрирования (3.32) при условии С_V = const, получим

,

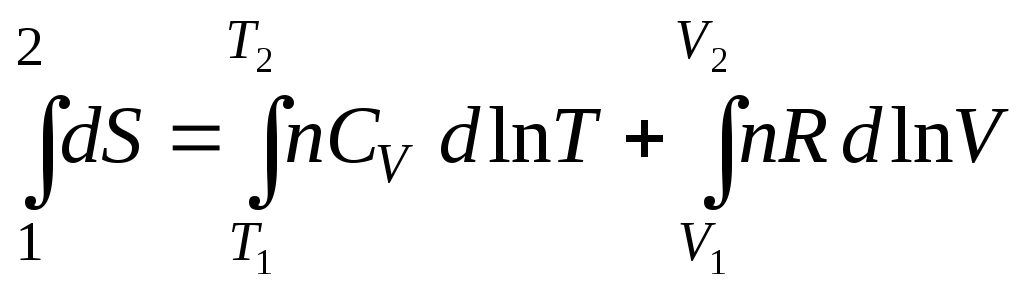. (3.33)

Так как

,

то изменение энтропии ΔS можно представить в виде функции давления и объема:

,

(3.34)

Так как

,

то изменение энтропии ΔS можно представить в виде функции температуры и давления:

,

(3.35)

При изотермическом расширении идеального газа (Т = const) из уравнений (3.33) и (3.35) получаем:

(3.36)

то есть при изотермическом расширении идеального газа энтропия увеличивается.

При нагревании идеального газа в изохорных или изобарных условиях энтропия также увеличивается:

, (3.37)

. (3.38)

Помимо вычисления изменения энтропии, важно определить значение энтропии S для одного моля идеального газа. Соответствующую формулу получим, исходя из уравнения (3.35) для 1 моля газа:

.

Примем, что Р₁ = Р^о (стандартное давление) и Т₁ = 1 К, тогда

, (3.40)

где – стандартная энтропия идеального газа при T = 1 К, которую называют энтропийной постоянной идеального газа и обозначают S′.

Индексы 2 в уравнении (3.40) можно отбросить, а само уравнение записать в виде

, (3.41)

где – относительное давление.

Стоящие под знаком логарифмов в уравнении (3.41) величины безразмерны. Энтропийная постоянная газа S′ может быть вычислена по молекулярным данным методами статистической термодинамики.

3.5.4. Изменение энтропии при смешении идеальных газов в изобарно-изотермическом процессе.

В смеси идеальные газы не взаимодействуют друг с другом и энтропия смеси идеальных газов будет равна сумме энтропий этих газов, когда каждый из них в отдельности занимает при температуре смеси тот же объем, что и вся смесь (теорема Гиббса). Если смешиваются n₁ моль первого газа, занимавшего объем V₁ при давлении Р, с n₂ моль второго газа, занимавшего объем V₂ при том же давлении Р, при постоянной температуре и общем давлении Р, то изменение энтропии при смешении ∆_mixS (подстрочный индекс от mixing – смешение) складывается из изменения энтропии каждого газа при его изотермическом расширении от объема V₁ (V₂) до объема V₁ + V₂. При этом парциальное давление каждого газа изменяется от Р до Р_i = P∙x_i (закон Дальтона для смеси идеальных газов, поскольку исходное давление каждого из газов равно конечному давлению смеси Р = Р_смеси), где х_i – мольная доля данного газа в смеси.

Изменение энтропии как функции состояния в результате смешения двух газов будет равно разности

,

где S_смеси – энтропия смеси газов, а S_исход – сумма энтропий газов до смешения. Энтропия газов до смешения S_исход в соответствии с уравнением (3.41) будет равна

, (3.42)

а энтропия смеси газов –

,

, (3.43)

где – относительное парциальное давление данного газа в смеси.

Тогда энтропия смешения газов будет определяться соотношением

(3.44)

Изменение энтропии при образовании 1 моль смеси идеальных газов будет равно

(3.45)

Согласно (3.45) ∆_mixS > 0, так как х_i < 1 и lnх_i < 0. Если смешивается n идеальных газов при Т, Р = const, то энтропия смешения в расчете на 1 моль смеси будет равна

. (3.46)

Следует обратить внимание, что энтропия газа при Т = const изменяется, если только изменяется его парциальное давление.

Уравнение для расчета энтропии смешения можно также легко получить как сумму изменений энтропий каждого газа при их изотермическом расширении до объема смеси:

. (3.47)

Из уравнения (3.47) следует, что возрастание энтропии при смешении двух идеальных газов зависит только от количества молей газов, но не зависит от их природы. В предельном случае, когда смешивается один и тот же газ, разделенный перегородкой на две части, увеличения энтропии, согласно (3.47), не должно происходить, так как парциальное давление газа не меняется и никакого термодинамического процесса не происходит. Таким образом, смешение двух идентичных газов нельзя рассматривать как предельный случай смешения двух различных газов. При переходе от образования смеси сколь угодно близких (различимых) газов к смеси одинаковых (неразличимых) газов ∆_mixS испытывает скачок. Это утверждение получило название парадокса Гиббса.