5.1. Применение доверительного интервала разности средних

Пусть имеются две выборки: выборка 1 и выборка 2. Надо решить вопрос: действительно ли они различаются? Неравенство выборочных средних, т.е. то, чтох₁ -х₂  0, еще не свидетельствует о неравенстве истинных средних генеральных совокупностей, к которым принадлежат эти выборки, т.е. о том, что ₁ - ₂ 0 (главным образом потому, что выборки из генеральной совокупности получают случайным образом).

Можно поставить вопрос иначе: больше ли доверительный интервал разности средних ДИ_х, чем сама разность средних х? Если это так, то при заданном уровне значимости статистически ощутимых различий между двумя выборками не существует и наоборот. Т.е. при ДИ_х  х выборки принадлежат одной генеральной совокупности (статистически значимых различий между ними нет, а при ДИ_х  х выборки принадлежат разным генеральным совокупностям.

ДИ разности средних вычисляют по формуле:

(19)

где n₁ и n₂ – объем первой и второй выборок соответственно,

t(,) – критерий Стьюдента, для вычисления которого уровень значимости  обычно принимают равным 0,025, а число степеней свободы  рассчитывают следующим образом:  = n₁ + n₂ – 2,

s_кол – коллективной стандартное отклонение, которое рассчитывают с учетом данных, входящих в обе выборки. Квадрат коллективного стандартного отклонения представляет собой коллективную дисперсию s²_кол:

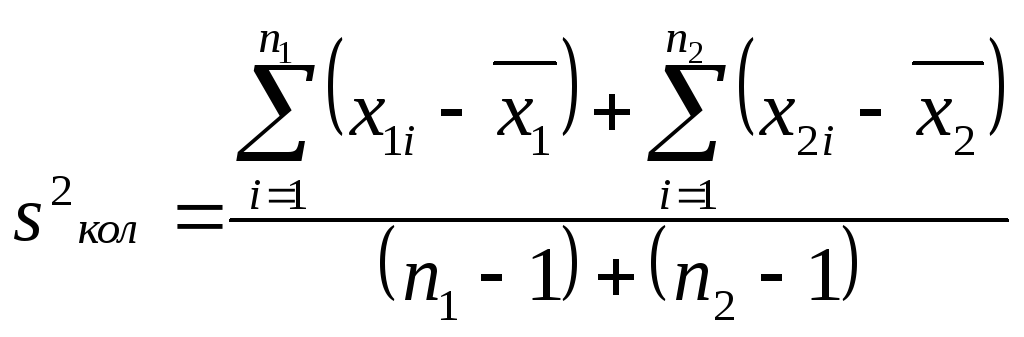(20)

Пример. Систематические измерения рН воды в фоновой и импактной зонах р. Волга привели к получению следующих результатов:

№ опыта	1	2	3	4	5	6	7	8	9
Выборка 1	8,67	8,61	8,66	8,66	8,52	8,66	8,65	8,65	8,67
Выборка 2	8,35	8,38	8,40	8,32	8,35	8,39	8,40

Есть статистически значимое различие между этими данными, полученными на значительном расстоянии друг от друга?

Рассчитаем выборочные средние по формуле (5) и разность между ними:

х₁ = 8,63;х₂ = 8,37; х = 8,63 - 8,37 = 0,26.

Используя формулу (20), вычислим коллективную дисперсию:

Тогда коллективное стандартное отклонение

Поскольку  = n₁ + n₂ – 2 = 9 + 7 – 2 = 14 и доверительная вероятность Р = 1 - 2 = =1 - 20,025 = 0,95, то с помощью табл. 2 Приложения находим критерий Стьюдента: t(0,025;14) = 2,14.

Находим величину доверительного интервала разности средних по формуле (19):

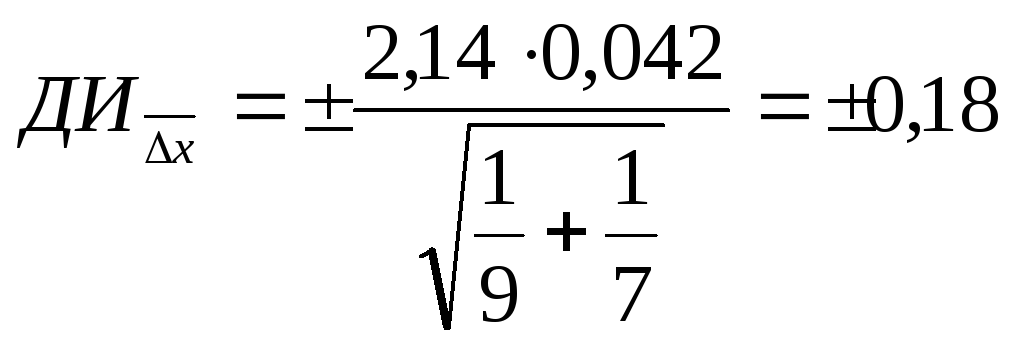
Таким образом, ДИ_х  х, что говорит о статистической значимости различий между полученными результатами, которая, скорее всего, обусловлена разными местами измерений.

5.2. Использование f – критерия. Сравнение дисперсий двух выборок

Корректный способ сравнения двух выборочных средних значений существует только для случая, когда обе серии значений имеют статистически одинаковые, т.е. незначимо различающиеся, дисперсии. Поэтому сравнению средних значений, как правило, предшествует сравнение соответствующих дисперсий.

Проверку нуль-гипотезы о незначимом различии двух дисперсий проводят с помощью F-критерия. Для этого вычисляют отношение

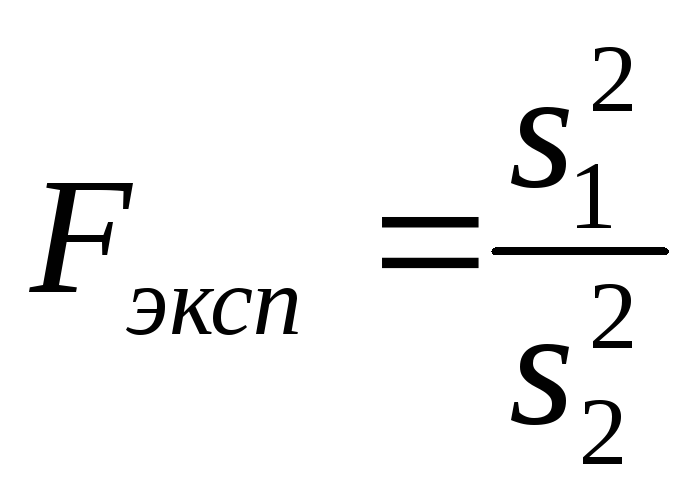(21)

где s²₁ – большая по значению дисперсия, s²₂ – меньшая. Поэтому значение F всегда больше единицы.

Если рассчитанное значение F_эксп не превышает табличное значение F_табл (см. табл. 3 Приложения), то для заданного уровня значимости и числа степеней свободы между дисперсиями не существует значимой разницы.

Т.е. при F_эксп  F_табл дисперсии однородны (выборки можно объединить в одну), а при F_эксп  F_табл дисперсии неоднородны (выборки объединять нельзя).

При незначимой разнице дисперсий находят средневзвешенную дисперсию

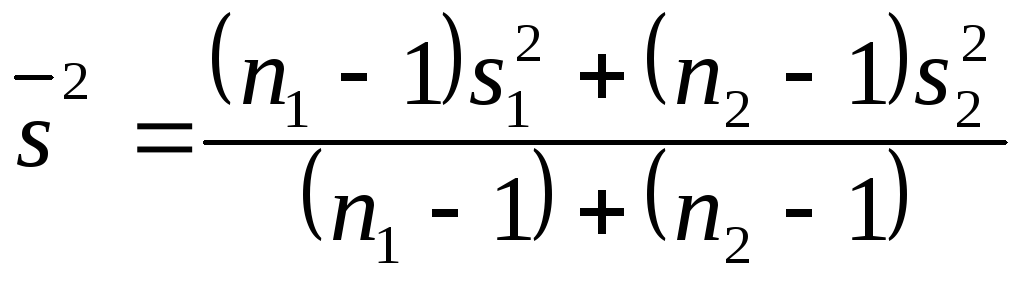(22)

а затем рассчитывают значение критерия Стьюдента

(23)

и сравнивают его с табличным значением коэффициента для заданного уровня значимости и числа степеней свободы  = n₁ + n₂ – 2. Если рассчитанное значение не превышает табличного, то различие между х₁ их₂ является незначимым. При этом все рассматриваемые результаты принадлежат одной выборке объемом n = n₁ + n₂, и их можно обработать совместно для нахождения общего среднего х и стандартного отклонения s. Напомним, что если объем такой объединенной выборки будет больше 20, можно рассчитанное значение s принять равным стандартному отклонению генеральной совокупности .

Пример. На территории промплощадки два сотрудника определяли концентрацию взвешенных веществ в воздухе. Первый получил следующие результаты: 38,20; 38,00; 37,66 мг/м³; второй – 37,70; 37,65; 37,55 мг/м³. Значимо ли различаются результаты, полученные разными людьми? Можно ли объединить выборки?

Сначала по формулам (5) и (6) вычислим выборочные средние и дисперсии:

х₁ = 37,95 мг/м³ ;х₂ = 37,63 мг/м³; s²₁ = 0,07453; s²₂ = 0,00583.

Проводим сравнение дисперсий по F-критерию с использованием формулы (21):

Сопоставляем это значение с табличным для ₁ = 2 и ₂ = 2, приняв  = 0,025 (Р = 0,95). Оно равно F_0,025;2;2 = 19,2  F_эксп, поэтому расхождение между дисперсиями незначимо.

Теперь установим, существует ли значимая разница между средними значениями. Рассчитаем значение средневзвешенной дисперсии по формуле (22):

Величина t по формуле (23): . Сравниваем полученное значение с табличным при  = 0,025 и  = n₁ + n₂ – 2 = = 3 + 3 – 2 = 4: t(0,025;4) = 2,78. Так как t  t_табл, то значимой разницы между средними значениями нет, поэтому две выборки можно объединить в одну, для которойх = 37,79 мг/м³; s = 0,25.