
- •Дисциплина «Мониторинг загрязнения опс»
- •Содержание
- •Введение
- •1. Погрешности. Общая характеристика и классификация
- •2. Случайные величины. Частота и вероятность появления результата
- •3. Нормальное распределение Гаусса и t-распределение
- •4. Порядок статистической обработки результатов измерений
- •Вычисление выборочных характеристик.
- •Вычисление доверительного интервала.
- •4.1. Исключение известных систематических погрешностей
- •4.2. Вычисление выборочных характеристик
- •4.3. Проверка распределения на нормальность методом асимметрии и эксцесса
- •4.4. Оценка наличия грубых измерений
- •4.5. Вычисление доверительного интервала
- •5. Проверка значимости гипотез
- •5.1. Применение доверительного интервала разности средних
- •5.2. Использование f – критерия. Сравнение дисперсий двух выборок
- •Приложение
- •Литература
4.3. Проверка распределения на нормальность методом асимметрии и эксцесса
Существуют различные методы проверки распределения на нормальность:
-
графические (построение вероятностной бумаги, построение гистограмм – диаграмм частоты накопления результатов анализа)
-
расчетные (с использованием 2 – критерия, метод асимметрии и эксцесса, метод Колмогорова-Смирнова и др.).
Все методы проверки (за исключением последнего) требуют достаточно большого объема численных данных.
Рассмотрим подробнее метод асимметрии и эксцесса, который помимо ответа на вопрос о нормальности распределения позволяет сделать выводе о его симметричности и пологости (заостренности). Последовательность проверки следующая:
-
Вычисление моментов
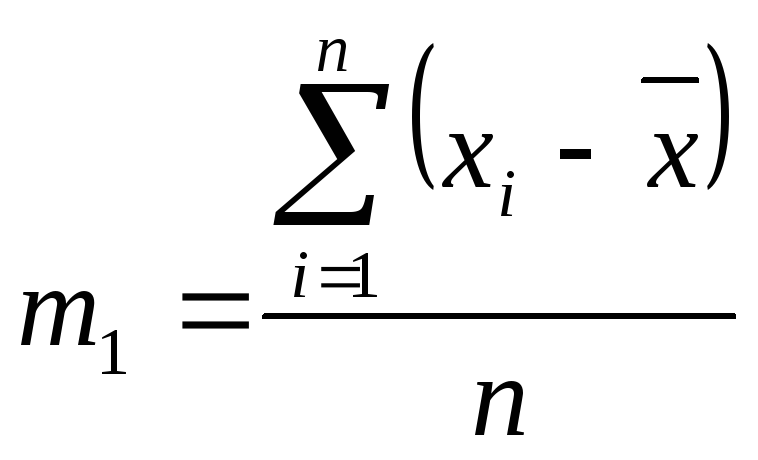 (8)
(8)
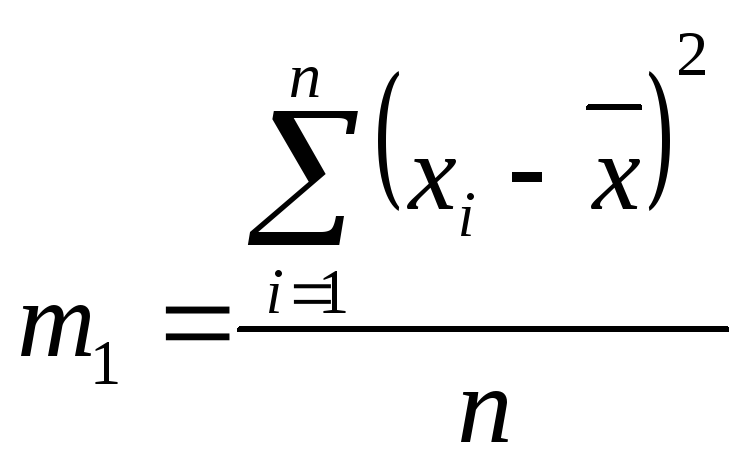 (9)
(9)
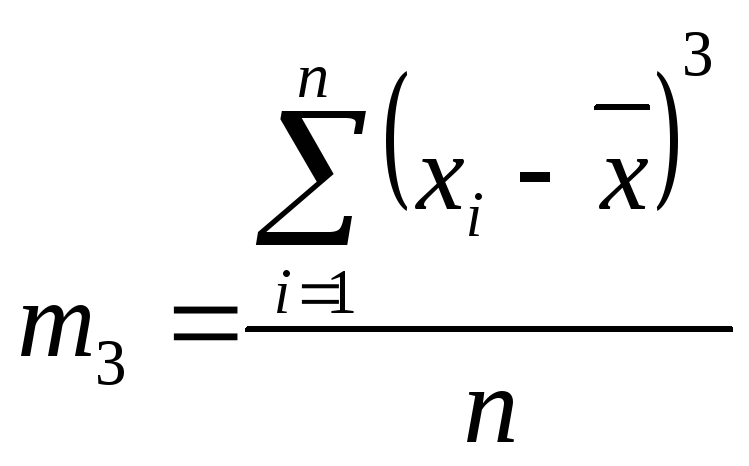 (10)
(10)
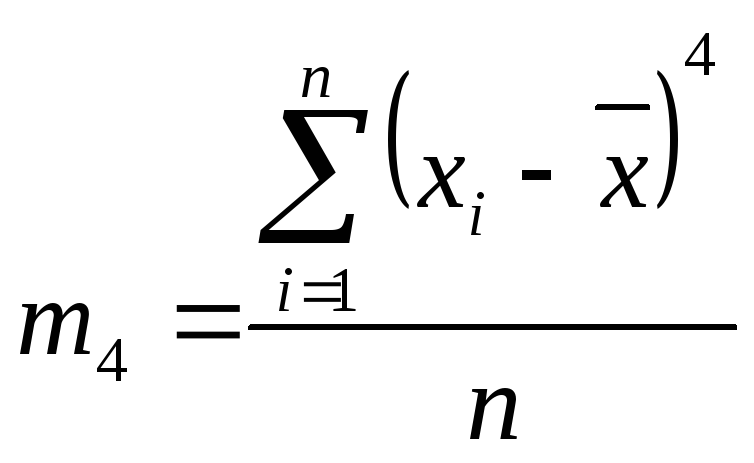 (11)
(11)
-
Вычисление значения асимметрии
![]() (12)
(12)
При g1 = 0 распределение является симметричным, при g1 0 наблюдается положительная асимметрия (см. рис. 2а), при g1 0 – отрицательная (см. рис. 2б).
(
 х)
(
х)
(
 х)
х)




х х
а - положительная асимметрия б - отрицательная асимметрия
Рис. 2. Асимметричные распределения.
-
Вычисление значения эксцесса
![]()
![]() (13)
(13)
Эксцесс характеризует пологость распределения.
При g2 = 0 распределение является нормальным по высоте, при g2 0 распределение заостренное, т.е. кривая имеет более высокую и острую вершину, чем нормальная, при g2 0 распределение пологое, кривая имеет более низкую и плоскую вершину, чем нормальная (см. рис. 3).
-
Вычисление несмещенной оценки асимметрии
![]() (14)
(14)
-
Вычисление несмещенной оценки эксцесса
![]() (15)
(15)
-
Вычисление среднеквадратичного отклонения для показателя асимметрии
![]() (16)
(16)
-
Вычисление среднеквадратичного отклонения для показателя эксцесса
![]() (17)
(17)
-
Проверка условий нормальности. Если одновременно выполняются два условия:
![]()
![]()
то, распределение считается нормальным для данной доверительной вероятности.
(х)

 заостренная
кривая
заостренная
кривая
 нормальная
кривая
нормальная
кривая
 пологая кривая
пологая кривая



х
Рис. 3. Нормальное, заостренное и пологое распределение.
4.4. Оценка наличия грубых измерений
Среди серии параллельных измерений могут встретиться значения, которые резко отличаются от остальных результатов и которые следовало бы отбросить как недостоверные. Однако сделать это можно лишь после предварительного исследования, т.к. необходимо выяснить, является ли данный результата следствием грубой погрешности (промаха). Существует несколько критериев для решения этого вопроса.
Простейший способ проверки основан на использовании правила трех сигм. В этом случае необходимо знать величину среднего арифметическогох и стандартного отклонения выборки s. Грубым будет считаться измерение, выпадающее за границы х 3s.
Наиболее предпочтителен для проверки так называемый Q-критерий. Для его использования необходимо сначала расположить все результаты серии измерений по ранжиру (т.е. в порядке возрастания или убывания):
х1 х2 х3 х4 … хn или х1 х2 х3 х4 … хn
Сомнительное значение может находиться либо в начале ряда (х1), либо в конце (хn).
Для этого значения находят разность между ним и ближайшим к нему значениями делят ее на размах варьирования = хn - х1.
Полученное значение Qэксп сравнивают со значением Qтабл, зависящим от выбранных доверительной вероятности Р и объема выборки n и взятом из специальной таблицы (Приложение, табл. 1). Доверительную вероятность для проверки промахов по Q-критерию обычно полагают равной 90%.
Если Qтабл Qэксп, то сомнительный результат следует сохранить.
Пример. При анализе проб воды получено содержание взвешенных веществ, мг/л: 55,95; 56,00; 56,04; 56,08; 56,23. Следует ли исключить последнее значение, т.е. является ли оно грубым промахом?
-
Используем правило трех сигм.
Определим выборочное среднее значение по формуле (5):
![]() мг/м3.
мг/м3.
Вычислим дисперсию по формуле (6):
![]() Поскольку
стандартное отклонение представляет
собой квадратный корень из выборочной
дисперсии, то
Поскольку
стандартное отклонение представляет
собой квадратный корень из выборочной
дисперсии, то
![]() мг/м3.
мг/м3.
Находим границы
интервала
![]() :
:
![]()
![]()
Так как все исходные данные входят в диапазон от 55,76 до 56,36 мг/м3, то грубых измерений нет.
-
Используем Q-критерий.
Рассчитаем размах варьирования: = 56,23 – 55,95 = 0,28.
Тогда
![]() .
.
Для n = 5 значение Qтабл при Р = 90% равно 0,56 (см. табл. 1 Приложения), т.е. Qтабл Qэксп. Результат следует оставить, он не является грубым измерением (промахом).
Таким образом, оба способа проверки дали аналогичные результаты.
