Види невизначеності:
EMBED
Equation.3
;
EMBED Equation.3
;
EMBED Equation.3
;
EMBED Equation.3
;
EMBED Equation.3
;
EMBED Equation.3
;
EMBED Equation.3
Розкриття невизначеності embed Equation.3
Невизначеність
виду EMBED Equation.3
може утворитись при обчисленні границі
функції, у якої в чисельнику і знаменнику
многочлени, при EMBED Equation.3
.
Для розкриття цієї невизначеності треба
чисельник і знаменник поділити на змінну
в самому високому степені, який міститься
в заданому виразі. Далі обчислюють знов,
використовуючи властивості границі та
властивості нескінченно великих і
нескінченно малих функцій.
Приклад 4. Знайти границю, не користуючись правилом Лопіталя:
EMBED Equation.3
Розв’язання.
Безпосереднім
підставленням маємо невизначеність
EMBED Equation.3
,
тоді ділимо чисельник і знаменник на
EMBED Equation.3
.
Маємо
EMBED
Equation.3
Розкриття
невизначеності
EMBED Equation.3
1) Невизначеність
виду EMBED Equation.3
може утворитись при обчисленні границі
функції, у якої в чисельнику і знаменнику
многочлени, при EMBED Equation.3
прямуючим до якогось скінченного числа.
В цьому випадку необхідно многочлени
в чисельнику і в знаменнику розкласти
на прості множники і скоротити.
Приклад 5. Знайти границю, не користуючись правилом Лопіталя:
EMBED Equation.3
Розв’язання.
EMBED
Equation.3
2) Також
невизначеність виду EMBED Equation.3
може утворитись при обчисленні границі
функції, у якої в чисельнику або/і
знаменнику знаходиться ірраціональність,
при EMBED Equation.3
прямуючим до якогось скінченного числа.
Тоді треба зробити перетворення для
позбавлення ірраціональності.
Приклад 6. Знайти границі, не користуючись правилом Лопіталя:
1)
EMBED
Equation.3
;
2)
EMBED
Equation.3
;
3)
EMBED
Equation.3
.
Розв’язання.
1)
EMBED
Equation.3
EMBED Equation.3
EMBED Equation.3
2)
EMBED
Equation.3
EMBED
Equation.3
EMBED
Equation.3
EMBED Equation.3
3)
EMBED
Equation.3
EMBED
Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
3) Невизначеність
виду EMBED Equation.3
може утворитись і при обчисленні границі
тригонометричних виразів. Для розкриття
невизначеності в цьому випадку заданий
вираз перетвореннями зводять до першої
важливої границі:
EMBED
Equation.3
.
Наслідки першої важливої границі:
1)
EMBED
Equation.3
;
2)
EMBED
Equation.3
;
3)
EMBED
Equation.3
.
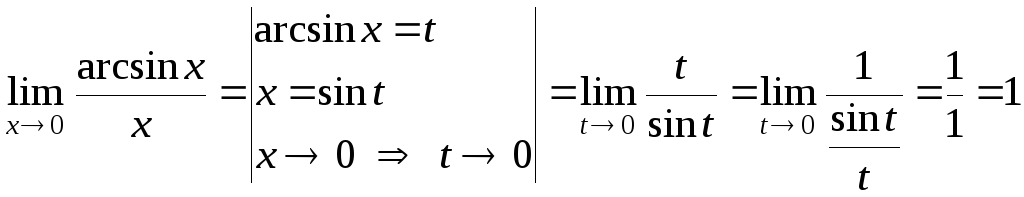Приклад 7. Знайти границі, не користуючись правилом Лопіталя:
1)
EMBED Equation.3
;
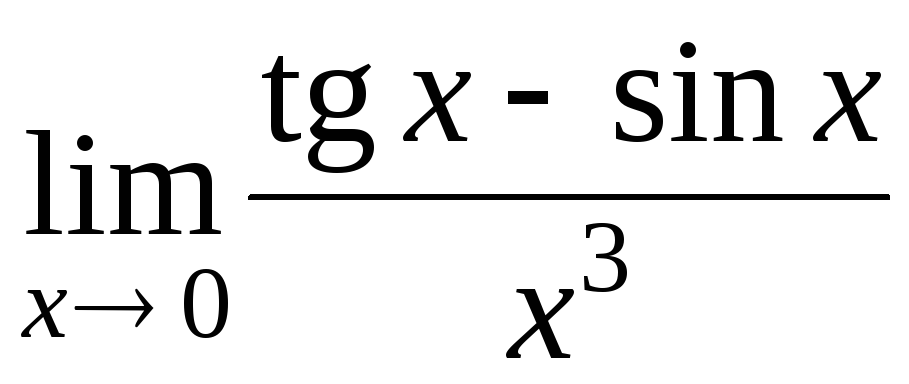2)
EMBED Equation.3
.
Розв’язання.
1)
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED
Equation.3
2)
EMBED Equation.3
EMBED
Equation.3
Розкриття невизначеності embed Equation.3
Невизначеність
виду EMBED Equation.3
утворюється при обчисленні границі
EMBED Equation.3
.
Позбавитись цієї невизначеності можна
скориставшись одним з двох способів:
1) звести
до другої
важливої границі:
EMBED Equation.3
або
її наслідків:
EMBED Equation.3
,
EMBED Equation.3
2) застосувати формулу
EMBED
Equation.3
Приклад 8. Знайти границю, не користуючись правилом Лопіталя:
EMBED
Equation.3
Розв’язання.
При застосуванні властивості 8 отримуємо
в основі виразу невизначеність виду
EMBED Equation.3
;
якщо її позбавитись за відповідним
правилом, то отримаємо EMBED
Equation.3
.
Далі
1 спосіб:
EMBED
Equation.3
EMBED
Equation.3
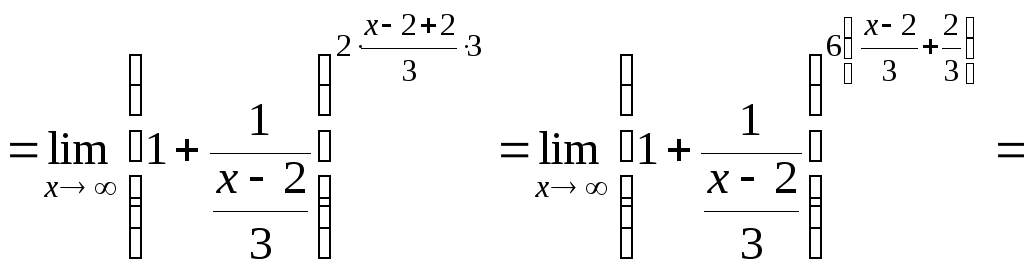
EMBED Equation.3
2 спосіб:
EMBED
Equation.3
EMBED Equation.3
