10.2. Оптимальное решение с учетом отношения к риску.

Для нахождения оптимального решения необходимо реализовать процедуры свертки и блокировки в формате построенного дерева решений.

Анализ при нейтральном отношении к риску. При нейтральном отношении к риску, как было отмечено в главах 5 и 6, используется критерий EVC. Расчет значений для показателя функции выбора такого критерия приведен в таблице 10.4. Дерево решений после процедур свертки по факторам «R» и «S» приведено на рис. 10.3.

Таблица 10.4. Расчет значений критерия EVC (f_n(σ,m) = m → max)

Фрагмент траектории	Концевые вершины для свертки	Расчет значения критерия EVC
Q1→R11→B	D1, D2, D3	=4215·0,9+4170·0,08+3945·0,02 = 4206
Q1→R13→B	D4, D5, D6	=4455·0,9+4410·0,08+4185·0,02 = 4446
Q1→R13→A1→S1→B	D7, D8, D9	=3564·0,9+3524·0,08+3324·0,02 = 3556
Q1→R13→A1→S2→B	D10, D11, D12	=3341·0,9+3301·0,08+3101·0,02 = 3333
Q1→R13→A2→S1→B	D13, D14, D15	=3802·0,9+3762·0,08+3562·0,02 = 3794
Q1→R13→A2→S2→B	D16, D17, D18	=3490·0,9+3450·0,08+3250·0,02 = 3482
Q2→R21→B	D19, D20, D21	=4695·0,9+4645·0,08+4395·0,02 = 4685
Q2→R22→B	D22, D23, D24	=4950·0,9+4900·0,08+4650·0,02 = 4940
Q2→R23→A1→S1→B	D25, D26, D27	=4059·0,9+4014·0,08+3789·0,02 = 4050
Q2→R23→A1→S2→B	D28, D29, D30	=3836·0,9+3791·0,08+3566·0,02 = 3827
Q2→R23→A2→S3→B	D31, D32, D33	=4297·0,9+4252·0,08+4027·0,02 = 4288
Q2→R23→A2→S4→B	D34, D35, D36	=3985·0,9+3940·0,08+3715·0,02 = 3976
Q3→R31→B	D37, D38, D39	=5160·0,9+5105·0,08+4830·0,02 = 5149
Q3→R32→B	D40, D41, D42	=5445·0,9+5390·0,08+5115·0,02 = 5434
Q3→R33→A1→S1→B	D43, D44, D45	=4554·0,9+4504·0,08+4254·0,02 = 4544
Q3→R33→A1→S2→B	D46, D47, D48	=4331·0,9+4281·0,08+4031·0,02 = 4321
Q3→R33→A2→S1→B	D49, D50, D51	=4792·0,9+4742·0,08+4492·0,02 = 4782
Q3→R33→A2→S2→B	D52, D53, D54	=4480·0,9+4430·0,08+4180·0,02 = 4470
Q1→R13→A1→S	(D7, D8, D9), (D10, D11, D12)	=3556·0,4+3333·0,6 = 3422
Q1→R13→A2→S	(D13, D14, D15), (D16, D17, D18)	=3794·0,65+3482·0,35 = 3685
Q2→R23→A1→S	(D25, D26, D27), (D28, D29, D30)	=4050·0,4+3827·0,6 = 3916
Q2→R23→A2→S	(D31, D32, D33), (D34, D35, D36)	=4288·0,65+3976·0,35 = 4179
Q3→R33→A1→S	(D43, D44, D45), (D46, D47, D48)	=4544·0,4+ 4321·0,6 = 4410
Q3→R33→A2→S	(D49, D50, D51), (D52, D53, D54)	=4782·0,65+4470·0,35 = 4673

Для расчета значения математического ожидания применительно к вершинам круглого типа «Фактор R» необходимо предварительно определить наилучшие размеры скидок (из анализируемых альтернатив А₁ и А₂) для каждого возможного варианта решений Q₁ - Q₃. Рисунки 10.3(а) и 10.3(б) иллюстрируют оптимальный выбор для указанных альтернатив А₁ и А₂. При этом для траекторий, проходящих через каждый вариант альтернатив Q (Q₁ - Q₃) при исходе, когда требуется принять решение о размере скидок на остаток продукции, оптимальным является выбор A₂.

Рис.10.3(а) Дерево решений после процедуры свертки при нейтральном отношении к риску

Рис.10.3(б) Дерево решений после процедуры свертки при нейтральном отношении к риску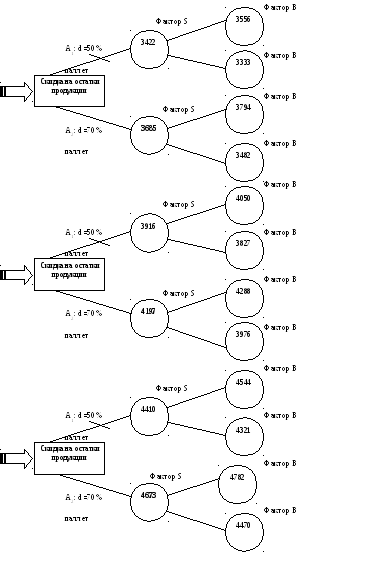

Действительно, для траектории Q₁→R₁₃→A₁→S значение показателя критерия EVC составляет 3422, а при прохождении через альтернативу А₂ (Q₁→R₁₃→A₂→S) значение показателя критерия EVC составляет 3685 (см. рис. 10.3(б)). Как видим, для траектории, проходящей через Q₁ в формате сценария R₁₃ для вершины «Фактор R», максимальное значение критерия EVC соответствует альтернативе A₂. Аналогичная ситуация имеет место и для траекторий, которые проходят через Q₂ и Q₃ (убедитесь в этом самостоятельно). Поэтому альтернативы А₁ во всех указанных трех случаях анализируемых траекторий (через Q₁ , Q₂, Q₃) необходимо заблокировать (см. рис.10.3(б)).

После того, как одна из альтернатив (A₁) для вариантов скидок на продукцию заблокирована, уже легко рассчитать величины математических ожиданий для вершин круглого типа «Фактор R». Соответствующие результаты приведены в таблице 10.5.

Таблица 10.5. Расчет значений критерия EVC (f_n(σ,m) = m → max) после процедуры свертки в формате вершин «Фактор R».

Фрагмент траектории	Концевые вершины для свертки	Расчет значения критерия EVC
Q1→R	(D1, D2, D3), (D4, D5, D6), (D13, D14, D15), (D16, D17, D18)	=4206·0,72+4446·0,26+3685·0,02 = = 4258
Q2→R	(D19, D20, D21), (D22, D23, D24), (D31, D32, D33), (D34, D35, D36)	=4685·0,28+4940·0,56+4179·0,16 = = 4747
Q3→R	(D37, D38, D39), (D40, D41, D42), (D49, D50, D51), (D52, D53, D54)	=5149·0,04+5434·0,42+4673·0,54 = = 5012

Как видим, лучший результат соответствует фрагменту траектории Q₃→R (он равен 5012 и выделен в таблице). Соответственно решения Q₁ (q=297) и Q₂ (q=330) необходимо заблокировать. Окончательный вариант дерева решений после всех процедур свертки и блокировки представлен на рис. 10.4. Указанный рисунок иллюстрирует следующее. При нейтральном отношении ЛПР к риску наилучшей альтернативой является Q₃ (заказ 363 паллет продукции). При этом в случае, если после реализации останется продукция на складе, оптимальный размер скидки – 70% (альтернатива A₂).

Анализ при осторожном отношении к риску. При осторожном отношении к риску необходимо в формате процедур свертки для каждой вершины круглого типа рассчитать значение критерия MVC, например, на основе соответствующей функции выбора вида f_s(σ,m) = m – k_s·σ². Величины математических ожиданий (m) уже были получены выше при расчетах в формате критерия EVC. Они были представлены в таблицах 10.4 и 10.5. Требуемые значения для величин дисперсий могут быть найдены стандартными методами самостоятельно (см. гл. 6, 9)

Напомним, что коэффициент индивидуальной осторожности к риску (k_s) можно определить по формуле: k_s = (m₂- m₁)/( σ₁²- σ₂²), где (m₁, σ₁) и (m₂, m₂σ₂) представляют эквивалентные для ЛПР соотношения мер риска и дохода в пространстве «Риск-Доход. Допустим, что для ЛПР являются эквивалентными варианты (m₁=4200; σ₁=100) и (m₂=5000; m₂=300), тогда получим:

k_s = (5000- 4200)/( 300²- 100²) = 0,01.

В результате, функция выбора будет иметь вид:

f_s(σ,m) = m – 0,01·σ².

Как и в случае анализа при нейтральном отношении к риску (критерий EVC), прежде чем рассчитать значение функции выбора по MVC критерию в вершинах круглого типа «Фактор R», необходимо определиться с оптимальным выбором одной из альтернатив А₁ и А₂ (скидки на единицу продукции). Для таких траекторий, проходящих через каждый из вариантов альтернатив Q₁ - Q₃ при исходе, когда надо принимать решение о размере скидок, оптимальным является выбор A₂. Поэтому альтернативы А₁ во всех указанных трех случаях необходимо заблокировать.

Лучший результат при таком отношении к риску уже, в отличие от анализа при нейтральном отношении к риску, соответствует фрагменту траектории Q₁→R. Соответственно решения Q₂ и Q₃ ( необходимо заблокировать. При осторожном отношении к риску (в формате заданной функции выбора) наилучшим решением является альтернатива Q₁ (заказ 297 паллет продукции). При этом, в случае, если после реализации останется продукция на складе, то оптимальный размер скидки снова (как и при нейтральном отношении к риску) составляет 70% (альтернатива А₂).

Содержание