
- •Лекция №6
- •2.1. Функция. Основные понятия, связанные с определением функции
- •2.2.Основные свойства функций
- •1. Ограниченность
- •2. Монотонность
- •3. Четность и нечетность
- •4. Периодичность
- •3.3. Основные элементарные функции и их графики. Класс элементарных функций
- •2.4. Обратные функции, обратимость строго монотонных функций
2.4. Обратные функции, обратимость строго монотонных функций
Пусть задана функция y=f(x)
с областью определения D
и множеством значений Е. Если каждому
значению y![]() E
соответствует единственное значение
x
E
соответствует единственное значение
x![]() D,
то определена функция x=φ(y)
с областью определения Е и множеством
значений D (см.рис.1.)
D,
то определена функция x=φ(y)
с областью определения Е и множеством
значений D (см.рис.1.)
Такая функция φ(y) называется обратной к функции f(x) и записывается в следующем виде: x=φ(y)=f -1(y). Про функции y=f(x) и x=φ(y) говорят, что они являются взаимообратными. Чтобы найти функцию x=φ(y), обратную к функции y=f(x), достаточно решить уравнение f(x)= y относительно x (если это возможно).
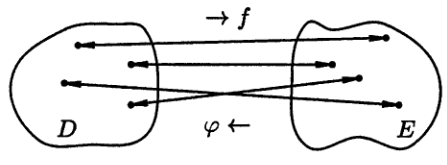
Рис.1.
Определение.
Функция, определенная
на множестве
![]() значений функции
значений функции
![]() ,
с областью значений, принадлежащей
множеству
,
с областью значений, принадлежащей
множеству
![]() ,
и ставящая в соответствие каждому
элементу
,
и ставящая в соответствие каждому
элементу
![]() его прообраз
его прообраз
![]() ,
называется обратной к
,
называется обратной к
![]() функцией и обозначается
через
функцией и обозначается
через
![]() .
.
Обратная
функция является, вообще говоря,
многозначной функцией. Если отображение
![]() является взаимно однозначным (см. п.
1.2), то обратная функция является
однозначной.
является взаимно однозначным (см. п.
1.2), то обратная функция является
однозначной.
Обратная
функция также является числовой функцией.
Если известно выражение функции
![]() ,
то выражение для
,
то выражение для
![]() получают следующим образом. Пишут
уравнение
получают следующим образом. Пишут
уравнение
![]() и решают его относительно
и решают его относительно
![]() .
При этом могут получиться несколько
выражений. Из них надо выбрать то,
значения которого принадлежат множеству
.
При этом могут получиться несколько
выражений. Из них надо выбрать то,
значения которого принадлежат множеству
![]() .
Получают равенство
.
Получают равенство
![]() .
Тогда
.
Тогда
![]() и будет выражением обратной функции.
Обычно в этом выражении заменяют
и будет выражением обратной функции.
Обычно в этом выражении заменяют
![]() на
на
![]() .
Выражение обратной функции не всегда
можно записать с помощью известных нам
функций. Поэтому операция образования
обратной функции может привести к
расширению запаса функций.
.
Выражение обратной функции не всегда
можно записать с помощью известных нам
функций. Поэтому операция образования
обратной функции может привести к
расширению запаса функций.
Теорема.
Пусть функция
![]() непрерывна и возрастает (убывает) на
промежутке
непрерывна и возрастает (убывает) на
промежутке
![]() и
и
![]() .
Тогда существует заданная на
.
Тогда существует заданная на
![]() обратная к
обратная к
![]() функция
функция
![]() ,
причем эта функция возрастает (убывает)
и непрерывна на
,
причем эта функция возрастает (убывает)
и непрерывна на
![]() .
.
Из определения обратной функции вытекает, что функция y=f(x) имеет обратную тогда и только тогда, когда функция f(x) задает взаимно однозначное соответствие между множествами D и E. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Заметим что функция y=f(x) и обратная ей x=φ(y) изображаются одной и той же кривой, т.е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т.е. аргумент) обозначить через x, а зависимую переменную через y, то функция обратная функции y=f(x) запишется в виде y=φ(x).
Это означает что точка М1(x0;y0) кривой y=f(x) становится точкой М2(x0;y0) кривой y=φ(x). Но точки М1 и М2 симметричны относительно прямой y = x (см. рис. 2). Поэтому графики взаимно обратных функций y=f(x) и y=φ(x) cсимметричны относительно биссектрисы первого и третьего координатных углов.
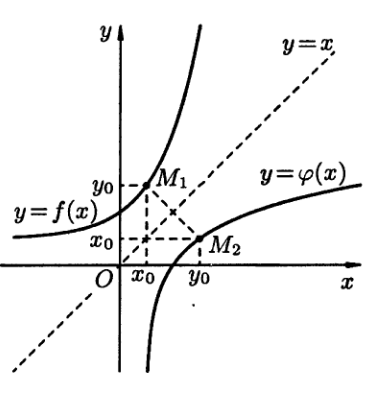
Рис.2.
Пример
1. Для функции y
= 2x
обратной функцией является функция
x = ![]() ;
;
Пример
2. Для функции y
=x 2
x![]() [0;1],
обратной функцией является x
=
[0;1],
обратной функцией является x
=![]() ;
;
Заметим,
что для функции y
=x 2,
заданной на отрезке [-1; 1], обратной не
существует, т. к. одному значению
y
соответствует два
значения x
(так, если y
=![]() ,
то x1
=
,
то x1
=![]() ,
x2
= –
,
x2
= –![]() ).
).
Пример
3. Найдем обратную
функцию для функции
![]() ,
,
![]() .
.
Решение.
Из уравнения
![]() находим
находим
![]() или
или
![]() .
Значениям
.
Значениям
![]() соответствуют значения
соответствуют значения
![]() ,
где
,
где
![]() .
Поэтому обратная функция задается
выражением
.
Поэтому обратная функция задается
выражением
![]() и определена на луче
и определена на луче
![]() .
Если заменить
.
Если заменить
![]() на
на
![]() ,
то получим
,
то получим
![]() ,
,
![]() .
Графики прямой и обратной функции
изображены на рис. 3.
.
Графики прямой и обратной функции
изображены на рис. 3.
Р ис.3
ис.3
Замечание.
Если точка
![]() принадлежит графику функции
принадлежит графику функции
![]() ,
то точка
,
то точка
![]() принадлежит графику функции
принадлежит графику функции
![]() ,
и обратно, из принадлежности точки
,
и обратно, из принадлежности точки
![]() графику функции
графику функции
![]() следует принадлежность точки
следует принадлежность точки
![]() графику функции
графику функции
![]() .
Но точки
.
Но точки
![]() и
и
![]() симметричны относительно прямой
симметричны относительно прямой
![]() .
Значит, графики функций
.
Значит, графики функций
![]() и
и
![]() симметричны друг другу относительно
прямой
симметричны друг другу относительно
прямой
![]() .
.
На рис.
47 изображены графики взаимно обратных
функций и показана их симметрия
относительно прямой
![]() .
.
