3.3. Основные элементарные функции и их графики. Класс элементарных функций

Функции: степенная (), показательная (), логарифмическая (, ), тригонометрические , , , и обратные тригонометрические функции , , и называются основными элементарными функциями. Напомним основные свойства и графики этих функций.

1. Степенная функция . В общем случае она определена и непрерывна при . При некоторых значениях степенная функция определена при или при , или и там и там. Рассмотрим различные случаи.

Пусть . Тогда при график степенной функции имеет вид, изображенный на рис. 19, при – на рис. 20, при – на рис. 21, при – на рис. 22.

Рис. 19 Рис. 20

Рис. 21 Рис. 22

Функция является обратной к функции , поэтому их графики симметричны относительно прямой (частный случай степенной функции). При график функции имеет вид, изображенный на рис. 23, а при – на рис. 24 (если ограничиться арифметическими значениями корня).

Р ис. 23 Рис. 24

Р ис. 25 Рис. 26 Рис. 27

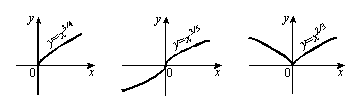
Рис. 28 Рис. 29 Рис. 30

Рис. 31 Рис. 32 Рис. 33

График функции , где , при касается оси , а при - оси . Если , то при неограниченном возрастании значение неограниченно убывает, а при неограниченном приближении к нулю неограниченно возрастает. При функция определена не для всех и . Если она определена при , то является четной или нечетной функцией, и потому ее график при получается из ее графика при с помощью той или иной симметрии. В качестве примера приведем графики функций при различных значениях и (рис. 25-33).

2. Показательная функция (). Она принимает положительные значения при всех значениях . Если , то . При показательная функция обращается в 1, так как . В случае показательная функция при неограниченном убывании аргумента неограниченно приближается к нулю, а при неограниченном возрастании аргумента функция неограниченно возрастает (рис. 34). Если же , то показательная функция при неограниченном возрастании аргумента неограниченно приближается к нулю, а при неограниченном убывании неограниченно возрастает (рис. 3 5).

Рис. 34 Рис. 35

Рис. 36 Рис. 37

3. Логарифмическая функция (, ). Она определена при . Функции и взаимно обратны друг другу, ибо и . Поэтому график логарифмической функции симметричен графику показательной функции относительно прямой .

Если , то логарифмическая функция возрастает, причем при неограниченном возрастании аргумента она неограниченно возрастает, а при неограниченном его приближении к нулю она неограниченно убывает (рис. 36). Если же , то логарифмическая функция возрастает, причем при неограниченном возрастании аргумента она неограниченно убывает, а при неограниченном его приближении к нулю она неограниченно возрастает (рис. 37). При любом , , имеет место равенство .

4. Основные тригонометрические функции , , , . Они связаны между собой соотношениями

, .

Ф ункции , определены на всей числовой оси и являются периодическими с основным периодом . При этом функция (рис. 38) является нечетной, а функция (рис. 39) является четной.

Рис. 38

Рис. 39

Ф ункция (рис. 40) не определена при , где . а функция (рис. 41) не определена при , где .При неограниченном приближении аргумента к этим точкам значения функций неограниченно возрастают по модулю. Функции , являются периодическими с основным периодом , а также нечетными.

Рис. 40

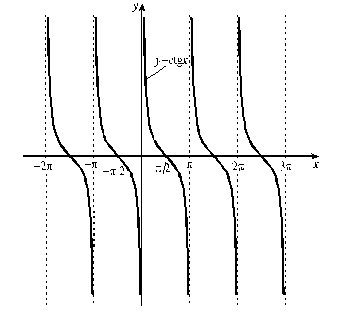
Рис. 41

5. Обратные тригонометрические функции. Так как они являются обратными для основных тригонометрических функций, то их графики симметричны относительно прямой графикам, изображенным на рис. 38-41. Обратные тригонометрические функции являются многозначными и обозначаются , , , .

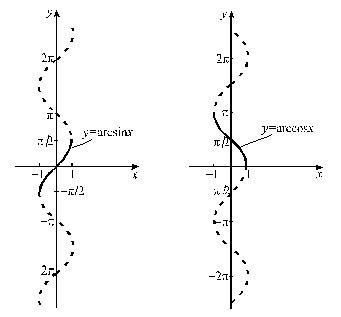
Рис. 42 Рис. 43

Однозначная функция (рис. 42) определена на отрезке и имеет область значений . Функция монотонно возрастает и является нечетной.

Однозначная функция (рис. 43) определена на отрезке и имеет область значений . Функция монотонно убывает.

Однозначная функция (рис. 44) определена на всей числовой оси и имеет область значений . Функция монотонно возрастает и является нечетной.

Рис. 44

Однозначная функция (рис. 45) определена на всей числовой оси и имеет область значений . Функция монотонно убывает.

Графики соответствующих многозначных функций изображены на рис. 42-45 штриховыми линиями.

Функции, которые можно получить при помощи конечного числа арифметических операций над основными элементарными функциями, а также их суперпозицией, называются элементарными. Во множестве элементарных функций выделяются следующие классы.

1. Многочлены (полиномы) – функции вида

.

Если , то целое неотрицательное число называется степенью многочлена . Функция, тождественно равная нулю, является в силу данного определения многочленом, ей не приписывается никакой степени. Многочлены определены на всей числовой оси.

Рис. 45

2. Рациональные функции – функции, представимые в виде , где и – многочлены ( – ненулевой многочлен). Функция определена во всех точках числовой оси, кроме тех точек, в которых знаменатель обращается в ноль.

3. Иррациональные функции, т.е. такие функции, не являющиеся рациональными, которые могут быть заданы композицией конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических действий. Например, функция иррациональная.

4. Трансцендентные функции – элементарные функции, не являющиеся рациональными или иррациональными. Например, функция трансцендентная.

Если известен график функции , то с его помощью легко получить графики следующих функций:

1) график функции получается сжатием графика вдоль оси в раз (при ) или растяжением в раз (при );

2) график функции – зеркальным отображением относительно оси ;

3) график функции – переносом параллельно оси на единиц вправо, если , и влево, если ;

4) график функции – растяжением вдоль оси в раз (при ) или сжатием в раз (при );

5) график функции – зеркальным отображением относительно оси ;

6) график функции – переносом параллельно оси на единиц вверх, если , и вниз, если ;

7) график функции – зеркальным отображением относительно оси участков графика , на которых ординаты отрицательны;

8) график функции – зеркальным отображением относительно прямой участка графика функции при .

Пример 1. Построить графики следующих функций:

а) ; б) ; в) ;

г) ; д) .

Решение.

а) График функции получается из графика сдвигом на три единицы вправо (рис. 46, а).

б) График функции получается сжатием графика вдоль оси в 4 раза (центр сжатия – прямая ), этот график также можно получить сдвигом графика на две единицы вверх, так как (рис. 46, б).

в) График функции получается из графика растяжением вдоль оси в два раза (рис. 46, в).

г) При построении графика функции участок кривой , расположенный ниже оси , отображается симметрично относительно этой оси (рис. 46, г).

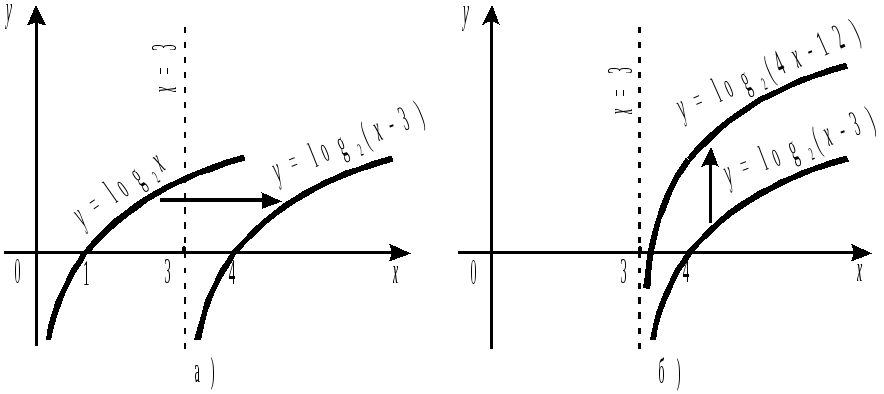
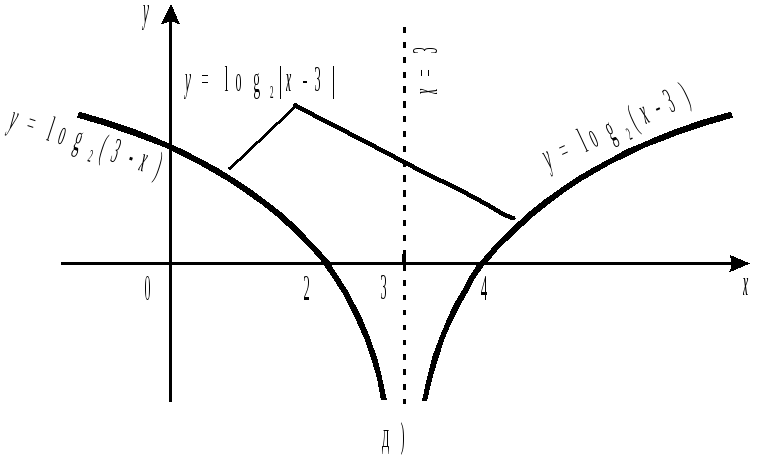
Рис. 46

д) График функции составляют две кривые: и симметричная ей относительно прямой (рис. 46, д).

Функция не обязательно должна быть задана явно – уравнением . Она может быть определена также неявно – уравнением или параметрически.

Пусть заданы функции и , непрерывные на некотором промежутке числовой оси. Уравнения

называются параметрическими уравнениями кривой в декартовой прямоугольной системе координат, если выполнено следующее условие: для всякого значения параметра точка принадлежит кривой и, наоборот, для всякой точки кривой существует такое значение параметра , что и .

Исключением параметра из параметрических уравнений уравнение кривой может быть представлено в неявном виде .

Пример 2. Исключением параметра найти уравнение заданной кривой и построить эту кривую

.

Решение. Если точка такова, что и для некоторого значения , то

,

т.е. точка принадлежит окружности , график которой известен. График также можно получить непосредственно из параметрических уравнений, воспользовавшись таблицей (табл. 3)

Таблица 3

и свойствами функций и при рассмотрении остальных значений параметра .