47.6 Конус второго порядка

Определение 47.11. Конусом второго порядка называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению

(47.8)

Отметим, что если координаты точки удовлетворяют уравнению (47.8), то и для любого действительного t координаты точки также удовлетворяют этому уравнению.

Поэтому, если точка лежит на конусе (47.8), то и вся прямая

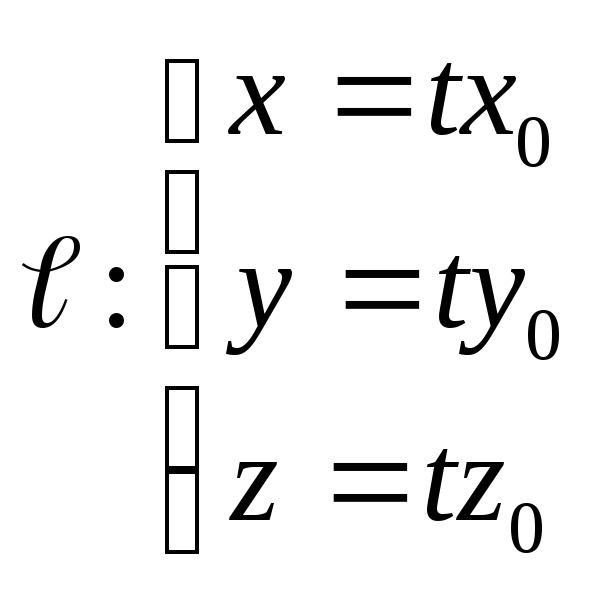(47.32)

(а это – параметрическое уравнение прямой, проходящей через точку и начало координат (см. параграф 42, уравнение (42.2)) также целиком находится на данной поверхности)

Определение 47.12. Эта прямая называется образующей конуса, а начало координат для уравнения (47.8) будет вершиной конуса.

Общий вид конуса изображён на рис.47.19

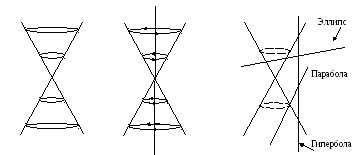
Рис.47.19 Рис.47.20 Рис.47.21

Отметим, что поверхность (47.33)

(если мы обе части равенства (47.33) возведём в квадрат, затем поделим на и всё перенесём в левую сторону, то получим уравнение (47.8)) является частью конуса (47.8), лежащей выше его вершины, а поверхность

(47.34)

частью конуса (47.8), лежащая ниже его вершины.

Конус (точнее - круговой конус) вращения можно получить, если мы одну из пары пересекающихся прямых (и не перпендикулярных друг другу) будем вращать вокруг другой из них (см. рис. 47.20).

В сечении конуса второго порядка плоскостями могут получиться (см. рис. 47.21 на котором как коническая поверхность, так и все секущие плоскости представлены как вид «сбоку»):

-эллипс (из рис. 47.21 видно, что в сечении конуса второго порядка плоскостью элипс получается некоторая ограниченная кривая второго порядка, т.е. эллипс; может получиться и окружность как частный случай эллипса);

-гипербола (из рис. 47.21 легко получить, что в сечении конуса второго порядка плоскостью гипербола должна быть некоторая разрывная кривая второго порядка, т.е. гипербола);

-парабола (получается в сечении конуса второго порядка плоскостью, параллельной его образующей, исходя из рис. 47.21, читателю предлагается самостоятельно доказать, что в этом случае в сечении должна получиться некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола);

-две пересекающихся прямых линии (получаются в сечении конуса второго порядка плоскостью, проходящей через две его образующих (естественно, эта плоскость должна проходить и через вершину конуса как точку пересечения его образующих));

-одна прямая линия (если плоскость проходит через одну образующую конуса второго порядка, т.е. касается поверхности);

-одна точка (вершина конуса второго порядка; для плоскости, проходящей через вершину конуса выше поверхности и ниже поверхности ).

Общее определение конической поверхности

Определение 47.13. Конической называется поверхность, удовлетворяющая следующему свойству

-существует такая фиксированная точка , лежащая на поверхности, что для любой точки M, также лежащей на этой поверхности, вся прямая, проходящая через точки M и , тоже находится на этой поверхности.

Определение 47.14. Точка в определении 47.13 называется вершиной конуса, а прямая из этого же определения носит название образующей конуса.

Определение 47.15. Уравнение (47.35) называется однородным, если из того, что числа удовлетворяют этому уравнению, следует, что и для любого действительного числа t значения также удовлетворяют уравнению (47.35).

Если вершиной конуса является начало координат (что всегда можно сделать, подобрав соответствующим образом оси координат), то из того, что точка удовлетворяет уравнению конической поверхности (т.е. лежит на этой поверхности), следует, что и координаты всей прямой линии , заданной уравнением (47.32), тоже должны удовлетворять уравнению этой поверхности, ибо, согласно определению 47.13, вся прямая , заданная уравнением (47.32), должна лежать на этой конической поверхности. Поэтому в некоторой системе координат уравнение конической поверхности должно быть однородным.

Отметим также, что если точка M лежит на образующей конической поверхности, то и симметричная ей относительно вершины конуса точка также должна находиться на этой же образующей и, следовательно, на данной поверхности. Поэтому всякая коническая поверхность является центральной, а вершина конуса должна быть его центром симметрии.

Задача: доказать, что из всех уравнений перечисленных в конце п.47.1, однородными уравнениями являются лишь (47.8), (35.21), (35.31), (35.20) и (47.7).

Уравнение (47.8) мы уже рассмотрели. Остальные уравнения будут рассмотрены в п.47.7.