Резонанс

Из решения видно, что при частоте вынуждающей силы равной частоте свободных колебаний оно не пригодно - возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде: . Подставим этот анзац в дифференциальное уравнение и получим, что :

Таким образом, колебания в резонансе будут описываться следующим соотношением:

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Увеличение амплитуды - это лишь следствие резонанса, а причина - совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям фазового синхронизма.

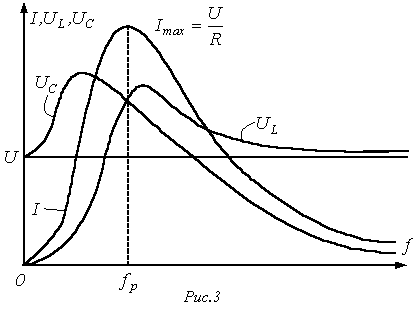
Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рис. 3 приведены типовые кривые I(f); и для цепи на рис. 1 при U=const.

Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:

,

(5)

 

- и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания .

Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением

,

(6)

или с учетом (4) и (5) для можно записать:

.

(7)

 

Эти законы, в частности, закон Ома и вытекающие из него правила Кирхгофа остаются справедливыми и в том случае, когда сила тока и напряжение меняются во времени. В этом случае в качестве значений силы тока и напряжения мы должны принимать их мгновенные значения I(t) и U(t). Для участка цепи закон Ома примет вид:

(3.41)

Эта зависимость справедлива в том случае, если изменения тока и напряжения происходят не слишком быстро, и для фиксированного момента времени мы можем считать силу тока в любом сечении проводника одинаковой. В действительности электрическое поле, создающее напряжение U(t), устанавливается в цепи не мгновенно, а распространяется вдоль цепи со скоростью света c. Если протяженность l электрической цепи невелика, время τ распространения поля вдоль этой цепи оказывается пренебрежимо малым по сравнению с характерным периодом Т, за который ток изменяется на сколь-нибудь заметную величину. Переменные токи в таких цепях называются квазистационарными. Для периодически меняющихся токов условие квазистационарности имеет вид:

τ = l/c << T (3.42)

Используемый в промышленных и бытовых целях переменный ток имеет частоту 50Гц. Условие квазистационарности в этом случае соблюдается для цепей длиной до сотен километров.

Рассмотрим процесс возникновения квазистационарного переменного тока в цепи, содержащей емкость и индуктивность (рис. 3.14). Такую цепь называют колебательным контуром.

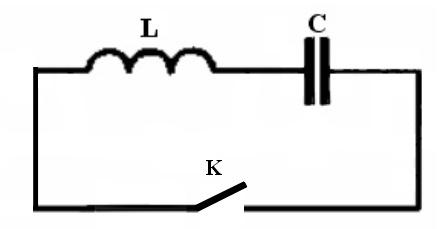
Рис. 3.14

Будем предполагать, что сопротивление проводов, составляющих колебательный контур, пренебрежимо мало. Сообщим предварительно конденсатору С электрический заряд q и замкнем ключ К, предоставив возможность конденсатору разряжаться через катушку. Заряженный конденсатор обладает энергией q²/2C. За счет этой энергии в цепи потечет электрический ток, создавая в катушке магнитное поле. Возрастающий магнитный поток внутри катушки за счет явления самоиндукции (по правилу Ленца) будет тормозить нарастание тока в цепи. Таким образом, конденсатор разрядится не мгновенно, а за определенное конечное время. За это время ток в цепи достигнет своего наибольшего значения I, и вся энергия электрического поля конденсатора перейдет в энергию магнитного поля катушки, равную LI²/2. Несмотря на то, что конденсатор окажется разряженным, ток в цепи не сможет прекратиться мгновенно, так как всякое уменьшение силы тока приведет к уменьшению магнитного потока, и за счет явления самоиндукции возникнет индукционный ток, поддерживающий ток в цепи в прежнем направлении. На поддержание этого индукционного тока будет расходоваться энергия магнитного поля катушки. В результате протекания указанного индукционного тока, на обкладках конденсатора начнет накапливаться заряд обратного знака. Этот заряд достигнет прежней величины q к моменту, когда вся энергия магнитного поля катушки будет израсходована на поддержание индукционного тока. В итоге этой фазы процесса энергия магнитного поля снова перейдет в энергию электрического поля конденсатора, заряженного обратным зарядом –q. С этого момента весь описанный процесс повторится снова, только ток потечет в обратном направлении. По завершению этой обратной фазы процесса конденсатор перезарядится до исходного заряда q, а ток примет нулевое значение.

Таким образом, в результате описанных электрических и магнитных процессов в колебательном контуре система самопроизвольно вернулась в первоначальное состояние, сохранив неизменным запас энергии. Теперь описанный цикл будет повторяться снова и снова неопределенно долго, при этом в цепи колебательного контура будет протекать переменный электрический ток. Графики изменения напряжения на конденсаторе и силы тока в катушке в течение одного периода колебаний представлены на рис. 3.15.

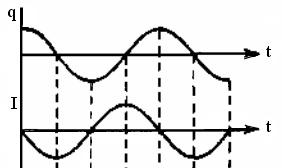
Рис.3.15

Описанный колебательный процесс можно сопоставить с механическими колебаниями математического маятника, в ходе которых потенциальная энергия шарика, отклоненного в крайнее амплитудное положение (аналог энергии заряженного конденсатора), переходит в кинетическую энергию шарика, пролетающего положение равновесия (аналог энергии магнитного поля катушки), и затем происходит обратное превращение. Мы знаем, что колебания маятника постепенно затухают под влиянием сил трения, превращающих механическую энергию колебаний в тепло. В реальном колебательном контуре, состоящем из проводников, обладающих электрическим сопротивлением, энергия электрического и магнитного полей также рассеивается, расходуясь на нагрев проводников.

Аналогия между маятником и колебательным контуром не только качественная. Уравнения, описывающие механические колебания маятника и электрические колебания в контуре математически идентичны.

Выведем уравнение электрических колебаний в контуре. Условно будем изображать контур состоящим из трех элементов: емкости С, индуктивности L и сопротивления проводов R (рис. 3.16).

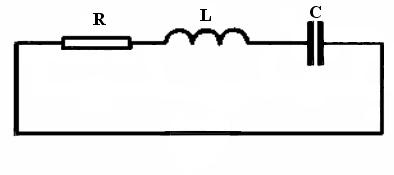
Рис. 3.16

В замкнутой цепи контура действует э.д.с. самоиндукции Е_c, сосредоточенная в катушке. При протекании тока I на сопротивлении R и емкости С возникают падения напряжения U_R и U_C. По второму правилу Кирхгофа для замкнутого контура сумма падений напряжения равна э.д.с., действующей в контуре, то есть

U_R + U_С = Е_c (3.43)

Раскроем значения всех величин, входящих в (3.43).

, (3.44)

где q – заряд конденсатора. Силу тока I можно представить как , а производную - как . С учетом этого (3.44) можно преобразовать к виду

(3.45)

Это дифференциальное уравнение, описывающее колебания заряда конденсатора. Введем обозначения:

, (3.46)

Величину β также как и в случае механических колебаний называют коэффициентом затухания, а ω₀ – собственной циклической частотой колебаний.

С введенными обозначениями уравнение (3.45) примет вид

(3.47)

Уравнение (3.47) полностью совпадает с дифференциальным уравнением гармонического осциллятора с вязким трением (формула (4.19) из раздела "Физические основы механики"). Решение этого уравнения описывает затухающие колебания вида

q(t) = q₀e^-tcos(t + ) (3.48)

где q₀ – начальный заряд конденсатора, ω = – циклическая частота колебаний, φ – начальная фаза колебаний. На рис. 3.17 показан вид функции q(t). Такой же вид имеет и зависимость напряжения на конденсаторе от времени, так как U_C = q/C.

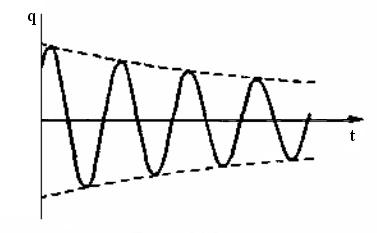
Рис. 3.17

Из рисунка видно, что амплитуда затухающих колебаний убывает со временем. Характеристикой затухания является время релаксации τ. Промежуток времени  = 1/ - это время, в течение которого амплитуда колебаний уменьшается в е раз. Затухание колебаний характеризуют также логарифмическим декрементом затухания λ

 = ln[A(t)/A(t+T)] = T= T/ (3.49)

где А(t) – текущая амплитуда колебаний (А(t) = q₀e^-t), Т – период колебаний. По своему смыслу величина, обратная T/ определяет число колебаний N_e, совершаемых за время релаксации. Следовательно, логарифмический декремент затухания - величина, обратная числу N_e.

Для характеристики качества колебательного контура вводят величину Q, называемую добротностью

Q = π/λ = πN_e (3.50)

Таким образом, добротность показывает, насколько медленно затухают колебания в контуре.

Из (3.50), (3.49) и (3.46) можно получить выражение для добротности контура через его электрические характеристики

Q = (3.51)

Описанный колебательный процесс в контуре совершается без каких-либо внешних воздействий за счет начального запаса энергии, сообщенного контуру. Такие колебания называют свободными. Электрическое сопротивление проводников приводит к затуханию свободных колебаний. Для получения незатухающих колебаний необходимо пополнять убыль энергии в контуре за счет внешних источников. Это можно осуществить, например, включив в состав контура источник переменной э.д.с. Е (рис. 3.18).

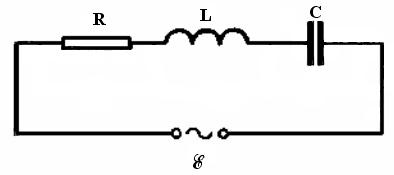
Рис. 3.18

Учтем наличие внешнего источника э.д.с. в дифференциальном уравнении, описывающем электрические процессы в контуре. Сумма падений напряжения на трех элементах контура L, R, C (поделенная на L) описывается левой частью уравнения (3.47). Но теперь, при наличии дополнительного источника э.д.с. Е, эта сумма согласно второму правилу Кирхгофа будет равна не нулю, а Е/L. Пусть э.д.с. Е меняется по гармоническому закону:

Е =U₀cosωt. (3.52)

Тогда дифференциальное уравнение процесса примет вид

(3.53)

Оно совпадает с дифференциальным уравнением вынужденных механических колебаний (уравнение (4.31) курса "Физические основы механики"). Решение этого уравнения в условиях установившегося процесса (t >> τ) описывает гармонические колебания с частотой ω внешнего источника э.д.с.

q(t) = q₀cos(t - ), (3.54)

где амплитуда колебаний заряда q₀ описывается выражением

(3.55)

Используя подстановки (3.46) выразим амплитуду через электрические параметры контура.

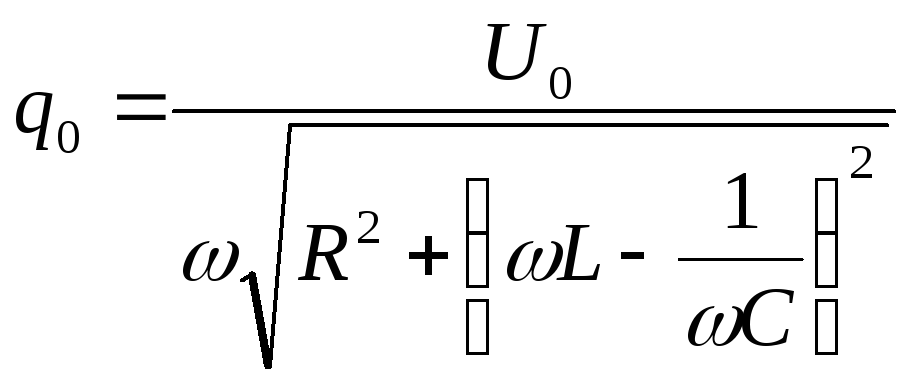(3.56)

Сила тока I в цепи контура равна , то есть

I(t) = -ωq₀sin(ωt-φ) (3.57)

Из (3.57) следует, что амплитуда I₀ колебаний тока равна ωq₀, то есть

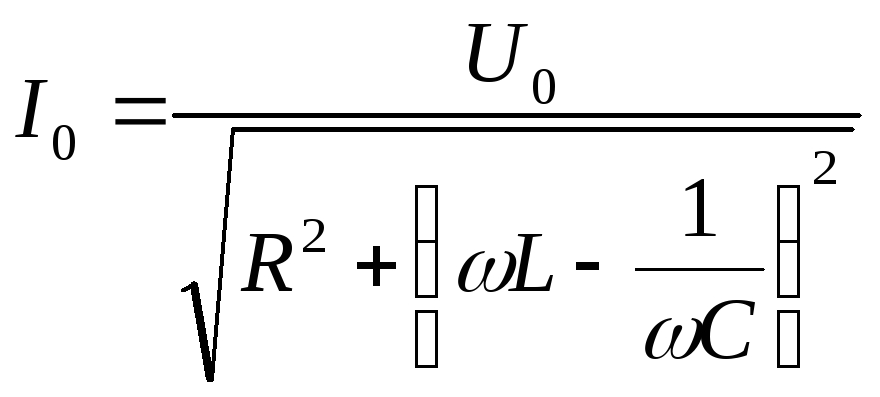(3.58)

Мы видим, что амплитуда I₀ зависит от частоты внешней э.д.с. График этой зависимости называется резонансной кривой. Примеры резонансных кривых представлены на рис. 3.19, где по оси абсцисс отложена частота источника э.д.с., а по оси ординат – амплитуда колебаний тока в контуре.

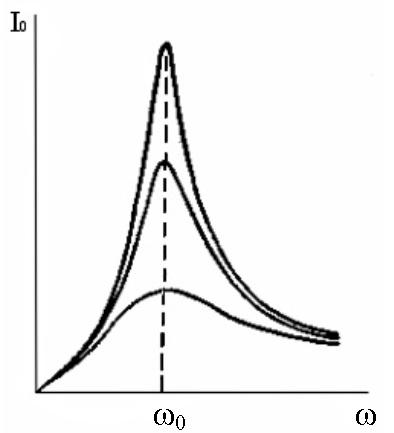
Рис. 3.19

Резонансные кривые имеет ярко выраженный максимум при ω = ω₀. Явление резкого возрастания амплитуды колебаний в контуре при совпадении частоты колебаний внешнего источника с собственной частотой контура называют резонансом. Острота резонансной кривой зависит потерь энергии в контуре. Чем больше потери, тем ниже максимум при резонансе. На рис. 3.19 приведены три резонансные кривые для различных потерь в контуре.

Введенная выше характеристика контура – добротность Q отображает остроту резонансной кривой. Остроту принято оценивать по условной ширине Δω кривой, определяемой на уровне , где I_om – амплитуда тока при резонансе, то есть максимум кривой. Построение, поясняющее определение величины Δω приведено на рис. 3.20. Можно показать, что при небольших потерях условная ширина Δω резонансной кривой связана с добротностью контура соотношением:

Q = ω₀/Δω (3.59)

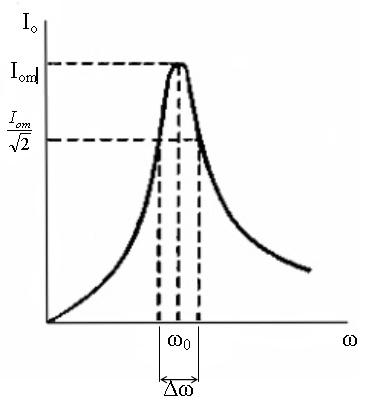
Рис.3.20

Можно показать также, что добротность контура показывает, во сколько раз амплитуда напряжения на конденсаторе при резонансе U_{C рез} превосходит амплитуду U₀ э.д.с. внешнего источника, то есть

Q = U_{C рез} /U₀

Это свойство колебательного контура значительно усиливать поданное на его вход переменное напряжение в случае совпадения частоты этого напряжения с собственной частотой контура используется для выделения сигналов определенной частоты на фоне большого числа прочих сигналов с другими частотами.
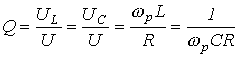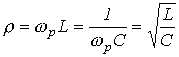