3. Индуктивность. Индуктивность соленоида. Явление самоиндукции.

На прошлой лекции были рассмотрены магнитные поля прямолинейного тока , соленоида (B = ₀nI (9.17)) и тороида .

Индукция каждого из этих полей пропорциональна силе тока, создающего поле.

В соленоиде поле однородно и вычислить поток вектора магнитной индукции, пронизывающий N витков соленоида, особенно просто:

.

Напомним, что здесь l, S — длина и площадь сечения соленоида, n = — число витков на единице длины соленоида.

. (10.4)

Магнитный поток, пронизывающий витки соленоида, пропорционален току, протекающему по его обмотке.

Можно показать, что этот частный результат справедлив не только для соленоида, но и для любого электрического контура.

Ток, обтекающий контур, создаёт магнитное поле. Это поле пронизывает контур, создавая поток, который пропорционален величине тока. Коэффициент пропорциональности, связывающий магнитный поток, пронизывающий контур, с током, протекающим по тому же самому контуру, называется индуктивностью контура L.

Например, индуктивность соленоида, как следует из (10.4):

(10.5)

Индуктивность любого контура зависит от его размеров и геометрии. В случае соленоида индуктивность определяется длиной и поперечным сечением соленоида, числом витков на единице длины (n), или полным числом витков N.

В системе СИ индуктивность измеряется в генри (Гн):

.

Теперь представим себе, что мы имеем возможность менять ток в соленоиде, передвигая ползунок А делителя напряжения (рис. 10.9.).

Рис.10.9.

Ток, протекающий в соленоиде, создаёт в нём магнитное поле. Это поле обеспечивает поток (см. 10.4.), причём скорость изменения магнитного потока будет пропорциональна скорости изменения тока:

.

Но изменение магнитного потока, пронизывающего замкнутый контур — единственное условие возникновения э.д.с. индукции:

.

Так как в данном случае изменение потока обусловлено изменением собственного тока, это явление электромагнитной индукции получило название явление самоиндукции:

. (10.6)

Э.д.с. самоиндукции пропорциональна скорости изменения тока в контуре. Закон самоиндукции (10.6) позволяет так определить единицу индуктивности 1 Гн:

.

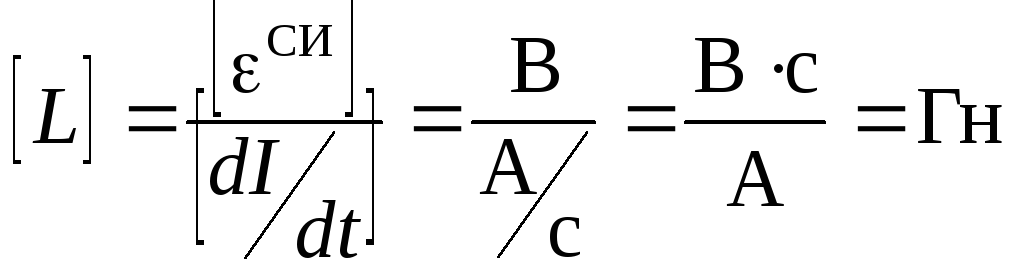1 генри — индуктивность такого контура, в котором возникает э.д.с. самоиндукции 1 В при скорости изменения тока в контуре 1 А/с.

4. Токи размыкания и замыкания цепи. Энергия и плотность энергии магнитного поля.

Посмотрим, как влияет э.д.с. самоиндукции на процесс установления тока в цепи, содержащей индуктивность.

В цепи, представленной на схеме 10.10, течёт ток. Отключим источник , разомкнув в момент времени t = 0 ключ К. Ток в катушке начинает убывать, но при этом возникает э.д.с. самоиндукции, поддерживающая убывающий ток.

Рис. 10.10.

Запишем для новой схемы 10.10.b уравнение правила напряжений Кирхгофа:

.

Разделяем переменные и интегрируем:

Пропотенцировав последнее уравнение, получим:

.

Постоянную интегрирования найдём, воспользовавшись начальным условием: в момент отключения источника t = 0, ток в катушке I(0) = I₀.

Отсюда следует, что c = I₀ и поэтому закон изменения тока в цепи приобретает вид:

. (10.7)

График этой зависимости приведён на рис. 10.11. Оказывается, ток в цепи, после выключения источника, будет убывать по экспоненциальному закону и станет равным нулю только спустя t = .

Рис. 10.11.

Вы и сами теперь легко покажете, что при включении источника (после замыкания ключа К) ток будет нарастать тоже по экспоненциальному закону, асимптотически приближаясь к значению I₀ (см. рис. 10.11.).

. (10.8)

Но вернёмся к первоначальной задаче размыкания цепи.

Мы отключили в цепи источник питания (разомкнули ключ К), но ток — теперь в цепи 10.8.b — продолжает течь. Где черпается энергия, обеспечивающая бесконечное течение этого убывающего тока?

Ток поддерживается электродвижущей силой самоиндукции  = . За время dt убывающий ток совершит работу:

dA = ^СИIdt = –LIdI.

Ток будет убывать от начального значения I₀ до нуля. Проинтегрировав последнее выражение в этих пределах, получим полную работу убывающего тока:

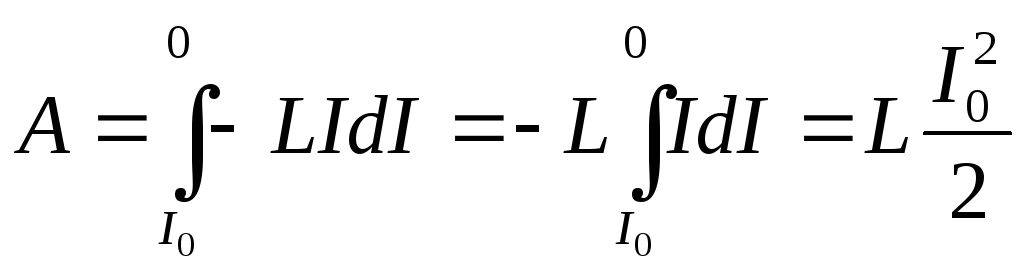. (10.9)

Совершение этой работы сопровождается двумя процессами: исчезновением тока в цепи и исчезновением магнитного поля катушки индуктивности.

С чем же связана была выделившаяся энергия? Где она была локализована? Располагалась ли она в проводниках и связана ли она с направленным движением носителей заряда? Или она локализована в объёме соленоида, в его магнитном поле?

Опыт даёт ответ на эти вопросы: энергия электрического тока связана с его магнитным полем и распределена в пространстве, занятом этим полем.

Несколько изменим выражение (10.9), учтя, что для длинного соленоида справедливы следующие утверждения:

L = ₀n²Sl (10.5) — индуктивность;

B₀ = ₀nI₀ (9.17) — поле соленоида.

Эти выражения используем в (10.9) и получим новое уравнение для полной работы экстратока размыкания, или — начального запаса энергии магнитного поля:

. (10.10)

Здесь V = Sl — объём соленоида (магнитного поля!).

Энергия катушки с током пропорциональна квадрату вектора магнитной индукции.

Разделив эту энергию на объём магнитного поля, получим среднюю плотность энергии:

[]. (10.11)

Это выражение очень похоже на выражение плотности энергии электростатического поля:

.

Обратите внимание: в сходных уравнениях, если ₀ — в числителе, ₀ — непременно в знаменателе.

Зная плотность энергии в каждой точке магнитного поля, мы теперь легко найдём энергию, сосредоточенную в любом объёме V поля.

Локальная плотность энергии в заданной точке поля:

.

Значит, dW = dV и энергия в объёме V равна:

.