3. Ряды распределения

Результаты сводки могут быть представлены в виде статистических рядов распределения.

Рядом распределения называют ряд цифровых показателей, представляющих распределение единиц совокупности по одному признаку, разновидности которого расположены в определённой последовательности.

Ряды распределения могут быть:

• атрибутивные - построенные по атрибутивному (качественному) признаку;

• вариационные - построенные по количественному признаку.

Вариационные ряды делятся на дискретные и интервальные.

Дискретный ряд распределения — это ряд, в котором варианты выражены конкретным числом.

Дискретный ряд может быть простым, когда каждое значение вариационного признака встречается в статистической совокупности только один раз, и взвешенным, когда каждое значение вариационного признака встречается в статистической совокупности определённое число раз. Количество одинаковых значений вариационного признака называется весом или частотой.

Интервальный ряд распределения — это ряд, в котором значения признака заданы в виде интервала.

Интервальные ряды распределения могут быть с равными интервалами и не равными интервалами. Интервальные ряды с равными интервалами встречаются чаще.

В общем виде рассмотренные ряды распределения можно представить следующим образом (п – объем совокупности; х_і – і-тое значение признака; f_i(j) – вес і-того значения признака):

а) дискретный простой; б) дискретный взвешенный; в) интервальный

xi		xi	fi		Группы по xi	fj
x1		x1	f1		х1н – х1в	f1
x2		x2	f2		х2н – х2в	f2
..		..	..		..	..
xi		xi	fi		хjн – хjв	fj
..		..	..		..	..
xn-1		xk	fk		хтн - хтв	fm
xn		Итого			Итого

Пример. Имеются следующие данные о рабочих экспериментального цеха завода.

Табельный номер рабочего	Профессия	Возраст, лет	Стаж работы по профессии, лет
1001	механик	23	3
1002	фрезеровщик	31	12
1003	слесарь	37	15
1004	механик	43	19
1005	слесарь-сборщик	35	12
1006	слесарь	50	15
1007	фрезеровщик	52	28
1008	механик	40	19
1009	слесарь	27	7
1010	слесарь-лекальщик	33	15

Построить ряд распределения: а) по профессиям рабочих; б) по возрасту; в) по стажу роботы.

а) ряд распределения по профессиям рабочих:

Профессия (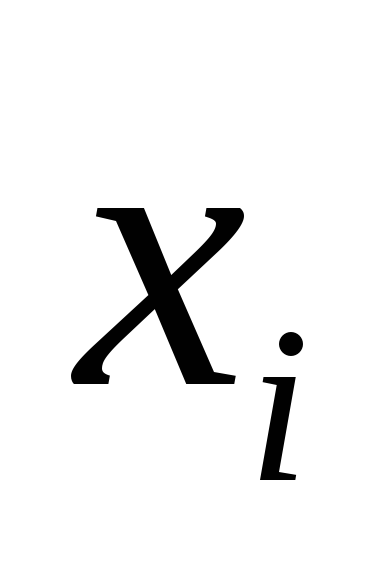)	Количество человек ()
механик	3
слесарь	3
слесарь-лекальщик	1
слесарь-сборщик	1
фрезеровщик	2
Итого	10

б) по возрасту в) по стажу работы

Возраст (), лет		Стаж работы (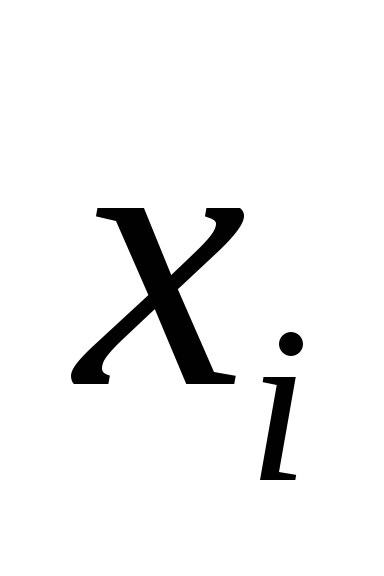), лет	Количество человек ()
23		3	1
27		7	1
31		12	2
33		15	3
35		19	2
37		28	1
40		Итого	10
43
50
52

В качестве весов в вариационных рядах могут использоваться:

1) абсолютная частота.

Абсолютной частотой в дискретных вариационных рядах называют число (количество) одинаковых значений признака (f_i^a).

Если обозначить объем совокупности через (п), то сумма абсолютных частот дискретного ряда будет равна:

,

где f_i^а – абсолютная частота і–того значения признака;

і=1, при этом k < n.

Абсолютной частотой в интервальных вариационных рядах называют число (количество) значений признака (f_j^a) попавших в определенный интервал (группу) (j).

Если обозначить объем совокупности через (n), число интервалов (групп) через (m), то сумма абсолютных частот интервального ряда будет равна:

.

2) относительная частота.

Относительная частота в дискретных вариационных рядах представляет собой отношение абсолютной частоты i–того значения варьирующего признака (f_і^a) к их общему количеству () выраженное в долях единицы или процентах.

Относительная частота дискретного ряда () получается из выражения:

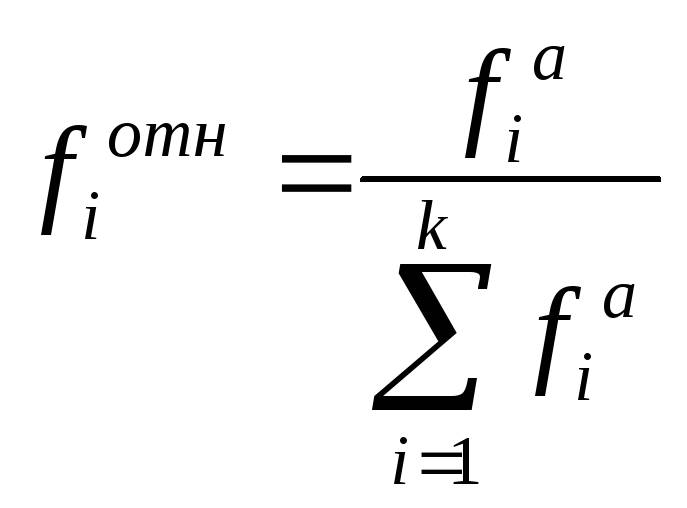, доли единицы

, %

Сумма относительных частот дискретного ряда равна:

1,00 или 100,0 %.

Относительная частота в интервальных вариационных рядах представляет собой отношение абсолютной частоты j–того интервала () к общему количеству значений варьирующего признака () выраженное в долях единицы или процентах;

, доли единицы;

, %

Сумма относительных частот интервального ряда равна:

1,00 или 100,0 %.