III. Неперервна випадкова величина

1. Неперервною випадковою величиною (н.в.в.) називається випадкова величина, що приймає всі дійсні значення ().

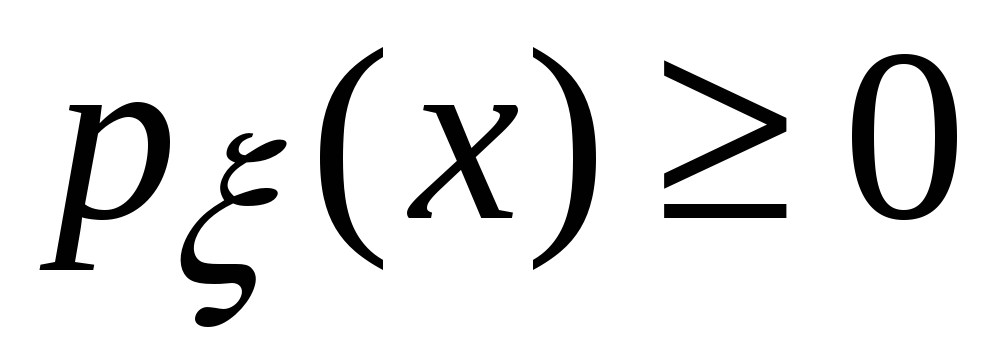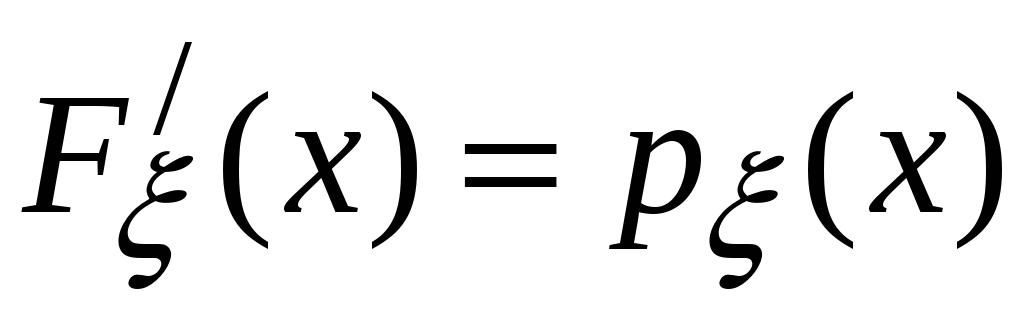2. Закон розподілу н.в.в. задається за допомогою двох функцій: а) щільність розподілу (диференціальна функція розподілу) , яка має наступні властивості: 1) ; 2) ; б) функція розподілу (інтегральна функція розподілу) , що визначається, як та має наступні властивості: 1) ; 2) ; 3) ; 4) ; 5) зростає на .

3. Імовірність потрапляння у проміжок. Зауваження. Для н.в.в. ймовірність отримати конкретне значення дорівнює нулю: Тому для н.в.в. розглядаються тільки вищезазначені інтервальні оцінки. Графічно ймовірність потрапляння у проміжок визначається в наступний спосіб: а) на графіку щільності розподілу б) на графіку функції розподілу

4. Математичне сподівання н.в.в.

5. Дисперсія н.в.в. або

Середнє квадратичне відхилення н.в.в. Властивості математичного сподівання та дисперсії н.в.в. такі самі, як у дискретному випадку. Приклади. 1) Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення н.в.в., щільність розподілу якої має наступний графік: Визначимо щільність розподілу аналітично Звідси .

2) Рівномірний розподіл на відрізку :

Тому

. Остаточно .

3) Показниковий розподіл з параметром :

Тому

за попереднім співвідношенням.

Звідси

.

Таким чином,

,

.

§4. Нормальний розподіл та його властивості

Одним з важливих прикладів н.в.в. є величини, що мають нормальний розподіл. Нормальному розподілу підкоряються багато випадкових величин, наприклад, похибка результатів вимірювань, багато результатів статистичних досліджень, тощо.

1. Щільність нормального розподілу:

.

2. Функція нормального розподілу:

.

3. Обчислимо математичне сподівання та дисперсію нормального розподілу.

де

- відома функція Лапласа,

(Оскільки функція - непарна, то ,

функція парна, тому .)

Аналогічно можна знайти, що

Таким чином, параметри нормального розподілу

,

,

тобто параметр - це математичне сподівання, а - середнє квадратичне відхилення н.в.в., що має нормальний розподіл.

Розглянемо центровану та нормовану величину

.

Вона має параметри . Такий розподіл називається стандартним нормальним розподілом.

Функція стандартного нормального розподілу:

.

Помітимо, що

.

Тоді для довільного нормального розподілу

.

Звідси ймовірність потрапляння у проміжок

Маємо формулу

Зауваження. Як бачимо, остання формула дуже схожа з інтегральною

формулою Муавра-Лапласа. Це не випадково, бо нормальний розподіл

наближає біноміальний, коли кількість випробувань прямує до нескінченості.

Знайдемо ймовірність того, що н.в.в. , яка має нормальний розподіл, відхиляється від мат.сподівання менше, ніж на :

за непарністю функції Лапласа.

Маємо формулу

Помітимо, що ймовірність того, що випадкова величина мало відрізняється від свого мат.сподівання , зростає, якщо зменшується параметр , тобто зменшується дисперсія. Таким чином, дисперсія – це міра розсіювання значень величини навколо середнього значення . Продемонструємо це графічно. Графіком щільності нормального розподілу є наступна крива, яка називається гауссіаною:

Як бачимо, це крива, симетрична відносно прямої , з вершиною у точці з координатами . Таким чином, дійсно, мат.сподівання є у певному розумінні середнім значенням н.в.в., що має нормальний розподіл. Якщо параметр зменшується, то вершина графіка піднімається вгору. Оскільки площа під графіком щільності розподілу завжди дорівнює 1, то гауссіана стає більш вузькою, значення величини більш згрупованими навколо середнього. Це підтверджує зміст дисперсії, як міри розсіювання значень навколо середнього.

Приклад. Обчислимо наступну ймовірність

.

Звідси випливає важливе у застосуваннях «правило трьох сигм»:

Подія, яка полягає у тому, що неперервна випадкова величина, яка має нормальний розподіл, відхиляється від свого математичного сподівання не менше, ніж на три величини середнього квадратичного відхилення, вважається практично неможливою.