§3. Довірчі інтервали

З розглянутих прикладів випливає, що ми не можемо однозначно визначити, чи буде дана функція законом розподілу, що відповідає вибірці, яка розглядається. Це пов’язане з тим, що одна вибірка може відповідати різним випадковим величинам, які мають різні закони розподілу. Єдине, що ми можемо визначити – чи може функція, що розглядається, бути законом розподілу, який відповідає даній вибірці, чи не може. Але й це ми можемо зробити лише з певною ймовірністю. Також і невідомі параметри відомого розподілу не можна визначити точно, а можна лише з певною ймовірністю оцінити їх значення.

Припустимо, що маємо вибірку об’єму . Функція розподілу відповідної випадкової величини залежить від невідомого параметру . Інтервал називається довірчім інтервалом для параметру , якщо ймовірність потрапляння в цей інтервал є сталою:

.

Величина називається довірчою ймовірністю.

Нехай випадкова величина розподілена нормально з невідомими параметрами і . Тоді результати §2 пп.2 и 3 можна інтерпретувати наступним чином:

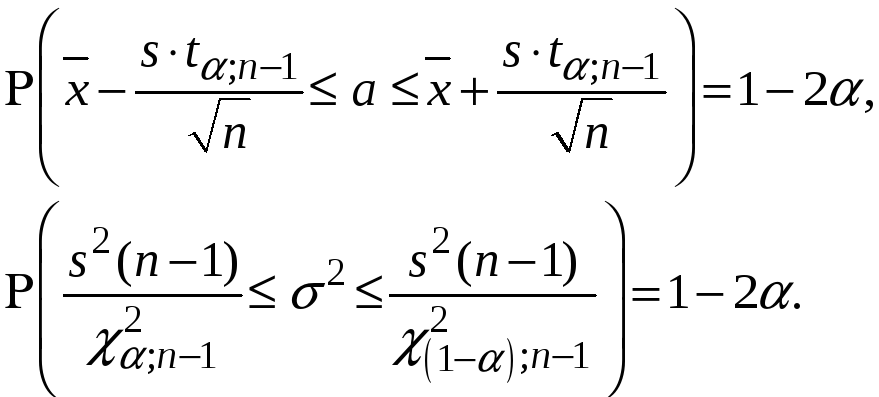
Отримані нерівності визначають довірчі інтервали для мат. сподівання та дисперсії нормально розподіленої випадкової величини за вибіркою. Тут - вибіркове середнє, - незміщена вибіркова дисперсія, - -границя розподілу Стьюдента с степенями вільності. - -границя розподілу Пірсона с степенями вільності. Значення границь можна знайти за таблицями (див. Додаток).

Приклад. Вибірка: . Об’єм .

Вважаємо, що випадкова величина розподілена нормально, знайдемо довірчі інтервали для мат. сподівання та дисперсії і . Довірчу ймовірність виберемо рівною . Тоді . Як обчислено раніше, , , . Знайдёмо за таблицями , , . Тоді з вказаних вище формул випливає, що довірчій інтервал для мат. сподівання:

.

Остаточно

.

Для дисперсії довірчій інтервал:

.

Остаточно

.

Як бачимо, інтервали доволі широкі.

§4. Вибіркова кореляція

І. Кореляційна таблиця

Припустимо, що спостерігаються значення, які набуваються двома випадковими величинами та . Маємо дві вибірки, які складаються

а) для : з , б) для : з , причому кожна пара значень спостерігається разів. Дані записуються у вигляді таблиці

		…
		…
…	…	…	…	…
		…
		…

де сума по рядках: - кількість появ значення у вибірці для ,

сума по стовпчиках: - кількість появ значення у вибірці для . Загальна кількість пар (кількість спостережень)

Тоді вибіркові середні та дисперсії обчислюються за правилами:

(запис скорочений)

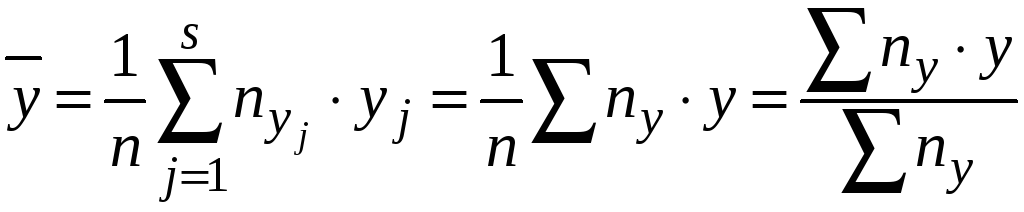
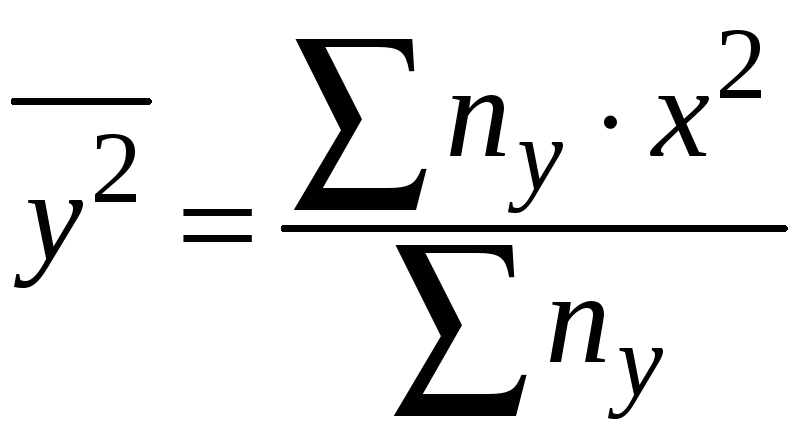
або

, - вибіркові середні квадратичні відхилення.

ІІ. Умовні вибіркові середні. Вибіркова регресія

Умовне вибіркове середнє - середнє арифметичне значень , що відповідають одному конкретному значенню :

- умовне середнє, що відповідає . Або скорочено:

Аналогічно для :

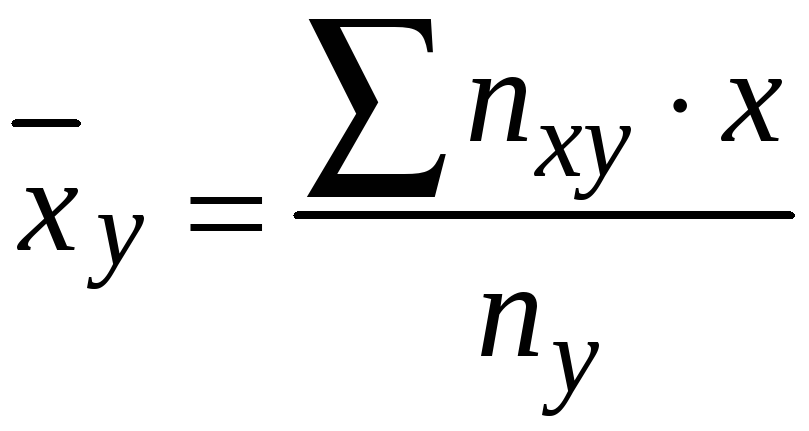
Вибіркова регресія на :

Вибіркова регресія на :

ІІІ. Вибірковий коефіцієнт кореляції

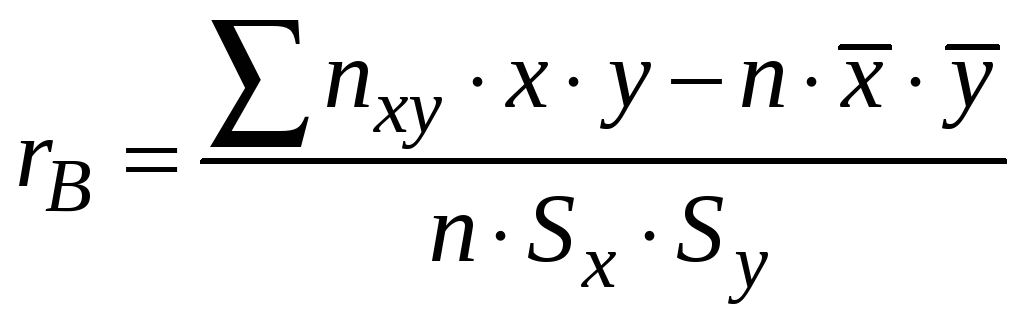
Вибірковий коефіцієнт кореляції є вибірковим аналогом коефіцієнта кореляції двох випадкових величин (див. §5 розд. Елементи теорії ймовірностей).

Зауваження. Вибірковий коефіцієнт кореляції не може бути по модулю більше одиниці.

В даному випадку також будуються лінійні наближення для вибіркової регресії –лінійні рівняння регресії на та на .

а) на

б) на

Помилка наближення оцінюється через вибіркове залишкове відхилення відносно

,

або відносно

.

Приклад. Задано кореляційну таблицю. Знайти вибірковий коефіцієнт кореляції, лінійні рівняння регресії на та на .

	10	3	2	15
	-	18	2	20
	10	21	4	35

Знайдемо суми по рядках та по стовпчиках: та , та загальну кількість спостережень .

Знайдемо вибіркові середні, дисперсії та вибіркові середні квадратичні відхилення за правилами:

,

Обчислимо вибірковий коефіцієнт кореляції за формулою

Для цього знайдемо

Тоді

Лінійне рівняння регресії на :

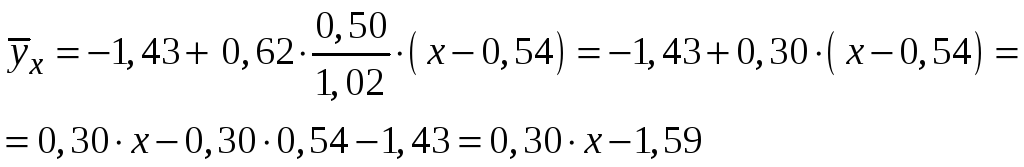
Остаточно

Лінійне рівняння регресії на

Остаточно

Вибіркове залишкове відхилення відносно

,

або відносно

.

Порівняємо значення та наближені значення умовних середніх:

За таблицею

За рівнянням регресії

За таблицею

За рівнянням регресії

Як бачимо, отримані значення непогано узгоджуються між собою та в цілому (крім ) знаходяться у межах залишкових відхилень.