§2 Задача перевірки статистичних гіпотез

1. Постановка задачі

Припустимо, що маємо вибірку об’єму . Закон розподілу відповідної випадкової величини невідомий. Висувається основна гіпотеза : випадкова величина розподілена за вказаним законом , та низка альтернативних гіпотез : випадкова величина розподілена за іншими законами: тощо.

У простішому випадку:

: випадкова величина розподілена за законом ,

: випадкова величина не розподілена за законом .

Припустимо, що ми маємо певний спосіб перевірки гіпотез (критерій). Тоді можливий один з 4 випадків:

1. Гіпотеза вірна, але відхиляється за критерієм (тобто приймається альтернативна гіпотеза );

2. Гіпотеза вірна та приймається;

3. Гіпотеза невірна та відхиляється;

4. Гіпотеза невірна, але приймається.

Як бачимо, у випадках 2) та 3) критерій спрацював правильно, а випадки 1) та 4) треба розглядати, як помилки.

Помилка 1 - гіпотеза вірна, але відхиляється – називається помилкою першого роду. Помилка 4 - гіпотеза невірна, але приймається – називається помилкою другого роду.

Як правило, за помилку першого роду беруть ту помилку, ціна якої більше. Виходячи з цього, відповідна гіпотеза вибирається за основну. Наприклад, нові ліки перевіряються на токсичність. Очевидно, за основну гіпотезу краще прийняти гіпотезу «препарат є токсичним». Дійсно, помилкою першого роду в цьому випадку буде класифікувати токсичний препарат, як нетоксичний. Ціною цього буде погіршення стану хворих, судові процеси, скандал, антиреклама і під кінець - можливе банкрутство. У випадку же помилки другого роду нетоксичний препарат буде прийнятий за токсичний, і в найгіршому випадку прийдеться починати все з початку, а то й лише відправити препарат на доопрацювання. Ціною будуть певні фінансові втрати, значно менші у порівнянні з втратами від помилки 1 роду.

Ймовірність помилки1 роду, тобто прийняття альтернативної гіпотези при тому, що вірною є основна гіпотеза ) позначається . Ймовірність помилки 2 роду - . Ясно, що ймовірність мусить бути малою. Зазвичай розглядають

,

де - рівень значущості критерію. Чим важливішими є наслідки помилки 1 роду – тим меншим беруть . Зазвичай розглядають тощо. Однак не треба зловживати зменшенням . Справа у тому, що у випадку завищеного рівня значущості критерій почне приймати без розбору велику кількість різноманітних нульових гіпотез, серед яких буде багато невірних – тобто зросте ймовірність помилки 2 роду, чого теж треба уникати.

2. Гіпотеза про параметри нормального розподілу : .

Припустимо, що маємо вибірку об’єму . Закон розподілу відповідної випадкової величини вважаємо нормальним, тобто функція розподілу має вигляд

,

де - математичне сподівання, и - дисперсія – невідомі. (Зазвичай в силу так званої центральної граничної теореми припущення про нормальність розподілу наприклад, результатів вимірювання при великій їх кількості, справджуються)

а) Висуваємо основну гіпотезу : математичне сподівання випадкової величини дорівнює даному числу (). Альтернативна гіпотеза : . Застосовуємо критерій Стьюдента. За вибіркою обчислюємо середнє і незміщену дисперсію . Позначимо

.

Виберемо значення . Тоді

при гіпотеза відхиляється на рівні значущості ;

при гіпотеза приймається.

При цьому ймовірність помилки 1 роду не більше :

.

Тут через позначено так звану -границю розподілу Стьюдента з степенями вільності. Значення її можна знайти за таблицею (див. Додаток).

б) Висуваємо : . Нехай : (одностороння альтернатива). Застосовуємо критерій Стьюдента. Позначимо

.

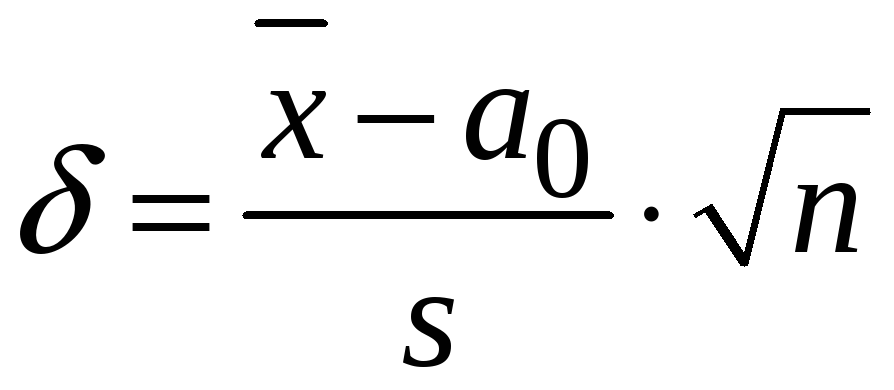Виберемо значення . Тоді

при гіпотеза відхиляється на рівні значущості ;

при гіпотеза приймається.

При цьому

.

Приклад. Вибірка: . Об’єм .

Варіаційний ряд: . Висуваємо гіпотезу , що відповідна випадкова величина розподілена нормально с параметром . За альтернативну гіпотезу візьмемо припущення . Таким чином, . Відомо , що (см. вище) обчислені за вибіркою середнє і незміщена дисперсія Обчислимо

.

Виберемо рівень значущості (двостороння альтернатива) тоді . Порівняємо обчислене відхилення та знайдену за таблицею розподілу Стьюдента величиною . Маємо

.

Гіпотеза приймається.