Елементи теорії ймовірностей

§1. Означення ймовірності

1. Простір елементарних подій Простором елементарних подій будемо називати довільну множину . Її елементи будемо називати елементарними подіями. Приклад. Підкидання гральної кістки один раз. Природно взяти , де за позначено результат випробування, що полягає у випадінні очок. Маємо шість взаємно виключних елементарних подій. Зауваження. Можна розглядати .

2. Випадкова подія 1) Випадковою подією будемо називати певну підмножину множини . Приклад. Підкидання гральної кістки один раз. В цьому випадку можна розглянути, наприклад, такі події: а) випадіння парного числа очок – вона відбудеться, якщо відбудеться елементарна подія або - природно вважати цю подію підмножиною , б) ) випадіння непарного числа очок – вона відбудеться, якщо відбудеться елементарна подія або - природно вважати цю подію підмножиною . 2) Сумою двох подій і називається об’єднання множин и . Дана подія полягає у тому, що відбулася щонайменше одна подія - або . 3) Добутком 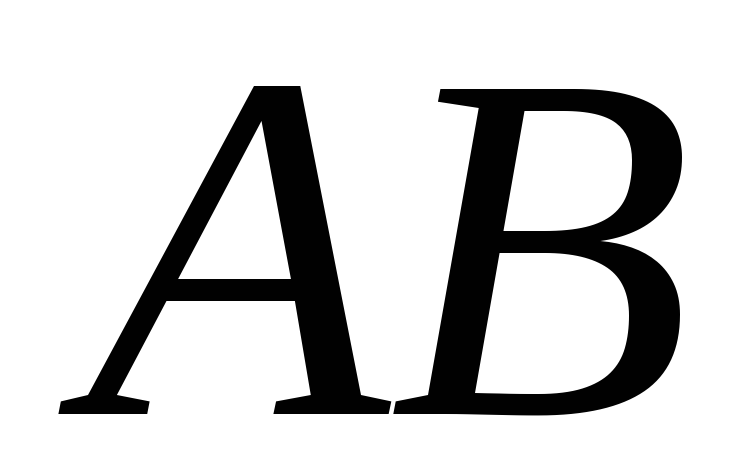двох подій і називається перетин множин і . Дана подія полягає у тому, що відбулися обидві події - і і . 4) Різниця 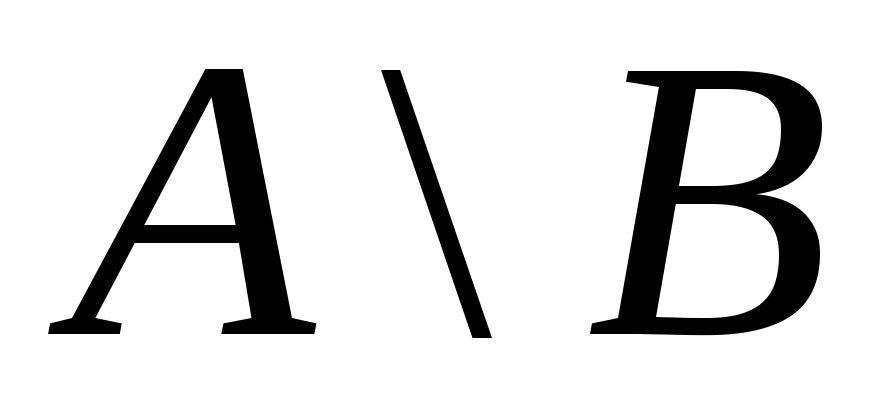двох подій і - це різниця множин і . Дана подія полягає у тому, що відбулася подія , але не відбулася подія . 5) Подія називається вірогідною (достовірною) 6) Порожня множина називається неможливою подією. 7) Подія називається протилежною події. Подія означає, що подія не відбулася. 8) Якщо множина є підмножиною множини (), то з відбування події випливає відбування події . 9) Якщо , то події і називаються несумісними. З відомих властивостей операцій над множинами випливають наступні властивості операцій над подіями: а) , г) , б) , д) , в) , е) . Імовірнісний зміст цих властивостей знайдіть самостійно.

3. Алгебра подій Алгеброю подій називається клас підмножин простору елементарних подій (позначимо його ), який має наступні властивості: 1) події , 2) якщо події , то , , . Приклади. 1) Система всіх підмножин простору є алгеброю подій (так званою максимальною алгеброю подій). Якщо містить елементів, то така алгебра складається з подій. Для простору результатів одного підкидання кістки можна записати всі події максимальної алгебри:

Ця алгебра складається з подій. 2) Система, яка містить тільки множини та також є алгеброю. Це мінімальна алгебра подій. Зазвичай розглядаються випадкові події, що належать деякій алгебрі подій.

4. Аксіоматичне означення ймовірності Числова функція , що визначена на алгебрі подій , називається ймовірністю, якщо вона задовольняє наступні умови (аксіоми ймовірності): А1. для будь-якої події з алгебри ; А2. ; А3. (аксіома скінченої адитивності). Якщо події і несумісні (), то

;

А4. (аксіома неперервності). Для будь-якої спадаючої послідовності подій з алгебри

що

,

має місце рівність

.

Зауваження. Властивість А4 виконується тільки у випадку нескінченної множини .

Простір , в якому вибрано алгебру подій і введено ймовірність , яка задовольняє аксіоми А1 –А4, називається ймовірнісним простором.

Відмітимо, що поняття ймовірнісного простору містить лише загальні вимоги щодо математичної моделі випадкового явища, і не визначають імовірність однозначно. Подальша конкретизація означення проводиться стосовно задачі, що розглядається.

Приклад. Підкидання гральної кістки один раз. Ми взяли , де алгебра подій складається зі всіх підмножин простору . Покладемо ймовірність кожної елементарної події рівною деякому числу , такому, що , тобто визначимо

.

Тоді за аксіомою А3 подія

матиме ймовірність

.

Зрозуміло, що виконується аксіома А1. Оскільки

,

то виконується і аксіома А2. В аксіомі А4 потрібності немає, оскільки множина є скінченою. Таким чином, всі аксіоми виконуються і наша числова функція дійсно є ймовірністю.

Подальша конкретизація моделі за допомогою тільки математичних засобів неможлива. Необхідно ввести додаткові положення, що віддзеркалюють відомі властивості (або властивості, що вважаються відомими) реального об’єкта, що досліджується. В даному прикладі природно вважати (якщо ми впевнені , що гра чесна), що кістка симетрична і випадіння різних її граней рівноймовірно. Тоді ймовірності елементарних подій рівні

і ймовірність визначено однозначно.

Якщо же ми вважаємо, що кістка належить шахраю та зроблена, наприклад, так, що кожного разу випадає тільки шісткою вгору, то треба покласти

.

Остаточний висновок про якість моделі, що вибрана, та ступінь її відповідності реальному процесові може бути зроблено тільки після експериментальної перевірки і стосується вже іншої науки – математичної статистики.