
- •Луганск 2007
- •10. Примеры обработки результатов измерений и варианты заданий для самостоятельной работы
- •10.1. Лабораторная работа №1. Тема: Построение графика линейной функции по результатам эксперимента (с использованием уравнения линейной регрессии). Ход работы
- •Лабораторная работа №2
- •Лабораторная работа №3.
- •Лабораторная работа №4.
- •Лабораторная работа №5.
- •Пример решения:
- •Лабораторная работа №6.
- •Пример решения:
- •Варианты заданий:
- •Лабораторная работа №7
- •Литература
Лабораторная работа №7
Тема: Обработка результатов совместного измерения.
Ход работы:
1. Функция температурной зависимости Rt = f(t) сопротивления катушки имеет вид:
![]() .
.
В результате эксперимента получены следующие результаты (заполнить таблицу согласно варианту):
|
|
t, C |
Rt, Ом |
|
1 |
20 |
|
|
2 |
30 |
|
|
3 |
40 |
|
|
4 |
50 |
|
|
5 |
60 |
|
|
6 |
70 |
|
|
7 |
80 |
|
Определить сопротивление R0 катушки при температуре 0 °С, значение температурного коэффициента расширения α и материала провода, которым намотана катушка.
Для
этого преобразуем формулу для
![]() :
:
![]() .
.
Тогда эту же формулу можно записать в виде:
![]() ,
(7.1)
,
(7.1)
где
![]()
![]() ;
;
![]()
![]()
![]() .
.
Условные уравнения (их количество – m = 7 для рассматриваемого случая по таблице с исходными данными) имеют вид:
![]() (7.2)
(7.2)
то есть:
![]() (7.3)
(7.3)
![]()
. . .
. . .
. . .
![]()
3. Составить систему нормальных уравнений и найти значения ее коэффициентов. Для n = 2 система нормальных уравнений имеет вид:
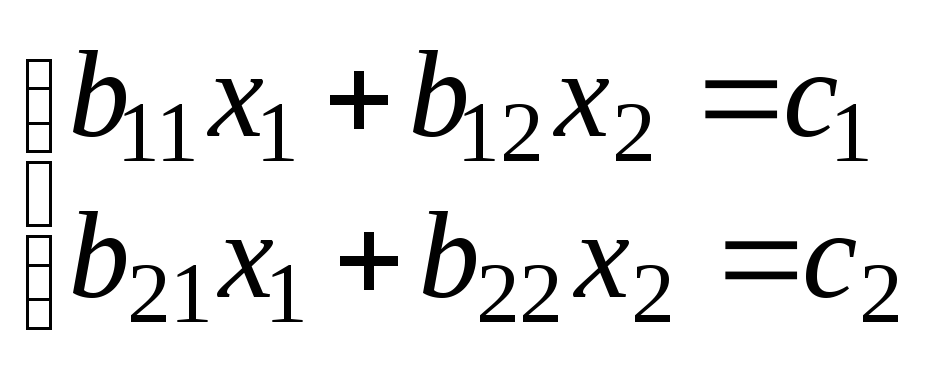 ;
(7.4)
;
(7.4)
где:
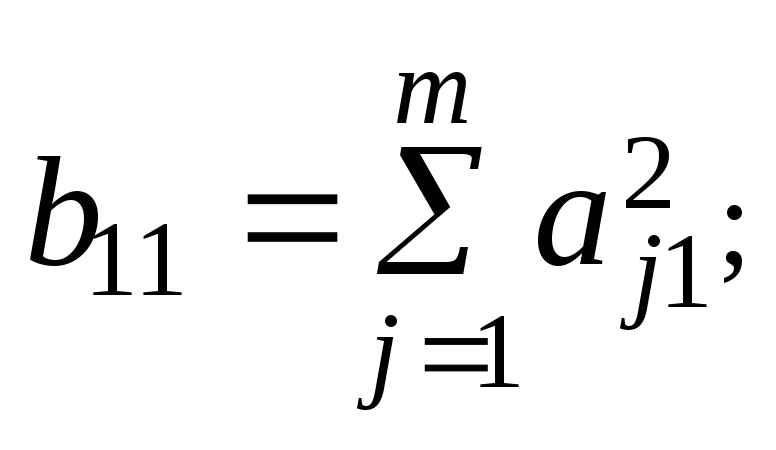 (7.5)
(7.5)
![]() ; (7.6)
; (7.6)
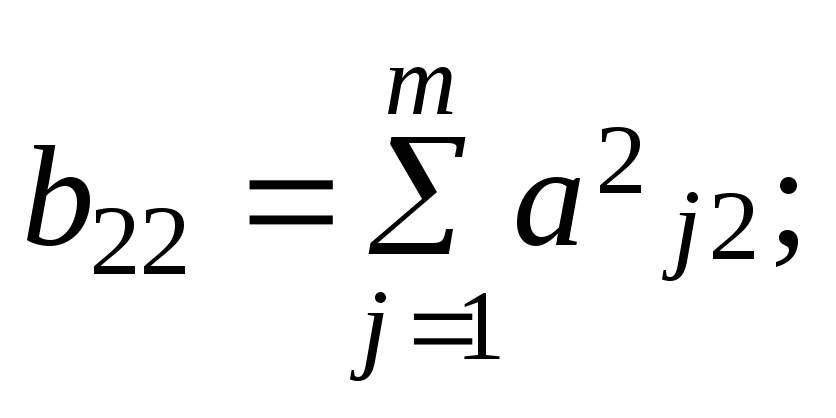 (7.7)
(7.7)
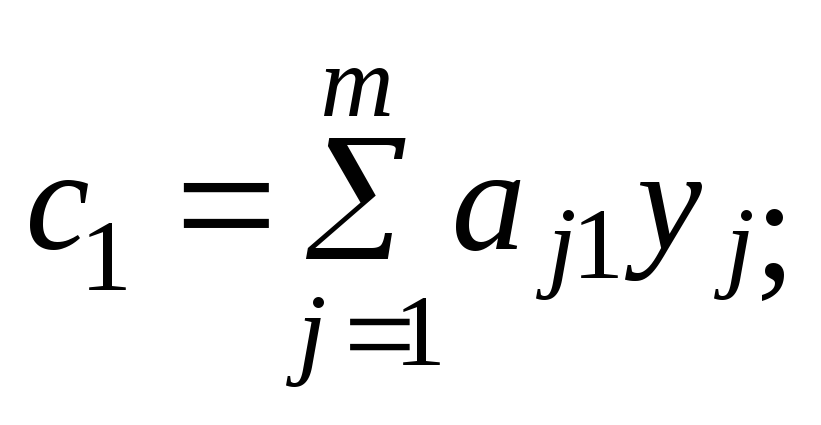 (7.8)
(7.8)
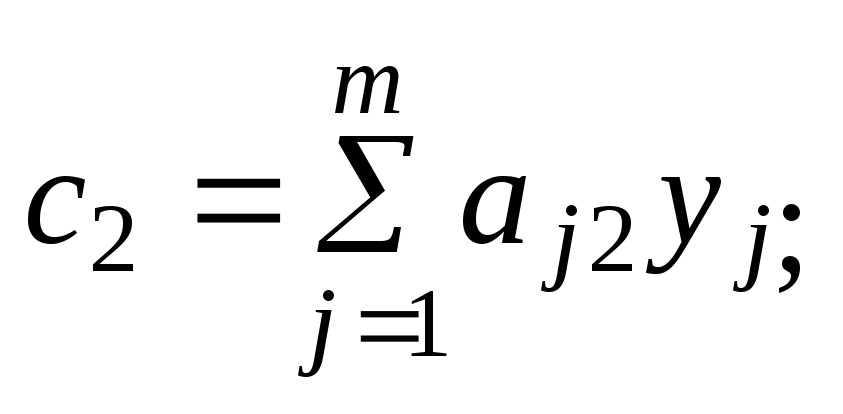 (7.9)
(7.9)
4.
Значения
![]()
![]() и
и
![]() можно определить с помощью определителей.
Главный определитель системы:
можно определить с помощью определителей.
Главный определитель системы:
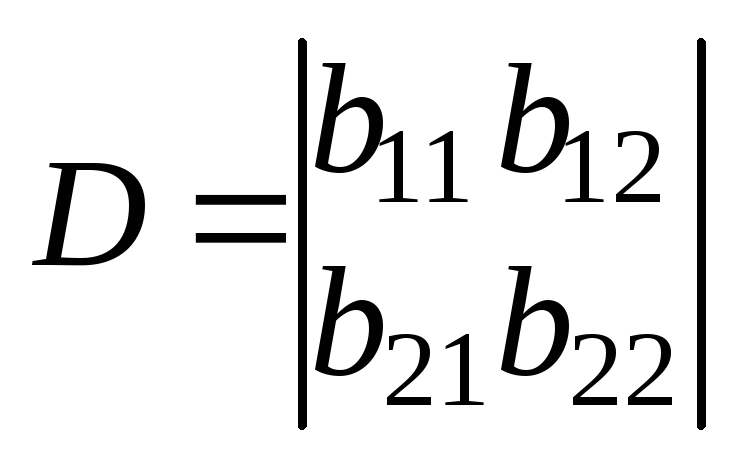 =
=![]() . (7.10)
. (7.10)
Частные определители:
![]()
![]() =
=![]() (7.11)
(7.11)
![]()
![]() =
=![]() (7.12)
(7.12)
Тогда:
![]()
![]() (7.13)
(7.13)
5.
Подставив наиболее вероятные значения
![]() и
и
![]() в условные уравнения, найти остаточные
погрешности j.
в условные уравнения, найти остаточные
погрешности j.
![]()
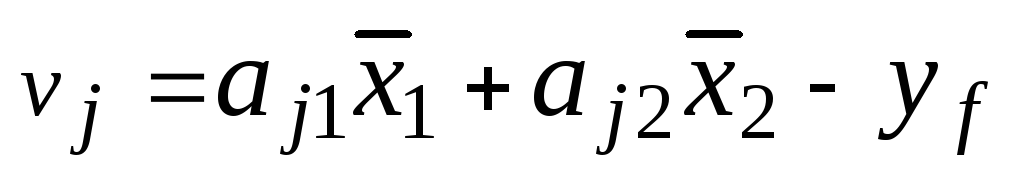 (7.14)
(7.14)
6. Найти среднеквадратические отклонения случайных составляющих погрешностей Sx1 и Sx2.
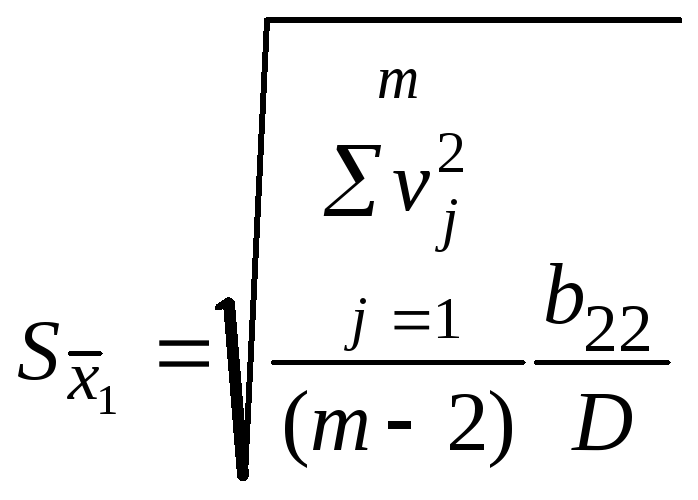 ;
;
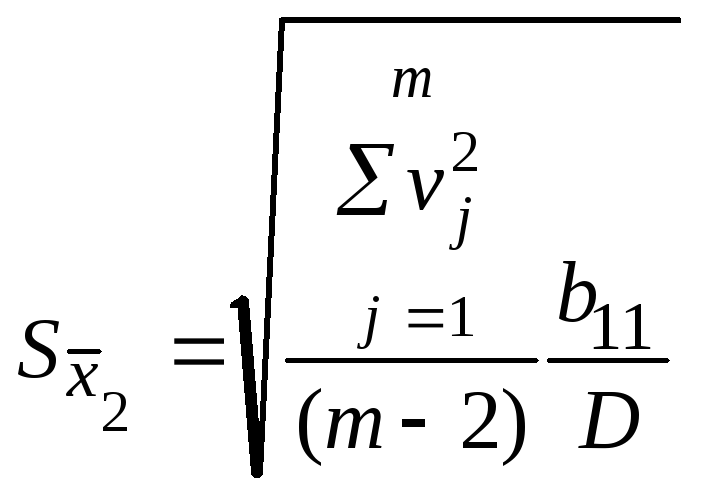 (7.15)
(7.15)
7. Найти надежные границы случайных погрешностей:
![]() ,
,
![]() (7.16)
(7.16)
где: t - табличное значение квантиля распределения Стьюдента для (m – n + 1) степеней свободы. Таблица квантилей распределения Стьюдента приводится в [1], стр.377, таблица №6, а также в конце этой задачи.
8. Найти результат косвенного измерения R0 и , используя формулы связи:
![]() ,
,
![]() (7.13)
(7.13)
В этом случае результат измерения сопротивления равен:
![]()
Результат измерения температурного коэффициента равен:
![]()
Пример решения:
(m=7; n=2):
|
t, °C |
Rt, Ом |
t, °C |
Rt, Ом |
|
20 30 40 50 |
26,06 27,09 28,12 29,17 |
60 70 80 |
30,19 31,23 32,26 |
Тогда для данного примера система условных уравнений по формулам (7.2), (7.3) имеет вид:
R0(1+20α)=26,06
R0(1+30α)=27,09
R0(1+40α)=28,12
R0(1+50α)=29,17
R0(1+60α)=30,19
R0(1+70α)=31,23
R0(1+80α)=32,26
Подставим в эти уравнения данные в соответствии с формулой (7.1) и для данного примера система условных уравнений примет вид:
х1+20х2=26,06
х1+30х2=27,09
х1+40х2=28,12
х1+50х2=29,17
х1+60х2=30,19
х1+70х2=31,23
х1+80х2=32,26
Находим коэффициенты нормальных уравнений:
![]() =
7;
=
7;
![]() =
=![]() =
350;
=
350;
![]() =
20300;
=
20300;
![]() =
204,12;
=
204,12;
![]() =
10495,5.
=
10495,5.
Тогда нормальные уравнения (7.4) имеют вид:
7x1+350x2 =204,12;
350x1+20300x2 =10495,5.
Средние
значения переменных
![]() и
и
![]() можно найти при помощи определителей.
Главный определитель системы по (7.10)
равен:
можно найти при помощи определителей.
Главный определитель системы по (7.10)
равен:
D
=
![]() =
(7 20300) – (350·350)
= 19600;
=
(7 20300) – (350·350)
= 19600;
Частные определители находим по выражениям (7.11), (7.12):
D1
=
![]() =
(204,12·20300)-(10495,5·350)
= 470211
=
(204,12·20300)-(10495,5·350)
= 470211
D2
=
![]() = (7·10495,5)-(350·204,12) =
2026,5
= (7·10495,5)-(350·204,12) =
2026,5
Находим средние значения переменных по формулам (7.13):
![]() =
D1/D
= 470211/19600 = 23,990357;
=
D1/D
= 470211/19600 = 23,990357;
![]() =
D2
/D
= 2026,5 /19600 = 0,10339285.
=
D2
/D
= 2026,5 /19600 = 0,10339285.
Подставляя
значения
![]() и
и
![]() в условные уравнения, вычисляем конечные
ошибки
в условные уравнения, вычисляем конечные
ошибки
![]() по
формуле (7.14):
по
формуле (7.14):
![]()
ν1 = х1 + 20х2-26,06 = -0,001786
ν2 = х1 + 30х2-27,09 = 0,0021425
ν3 = х1 + 40х2-28,12 = 0,006071
ν4 = х1 + 50х2-29,17 = -0,0100005
ν5 = х1 + 60х2-30,19 = 0,003928
ν6 = х1 + 70х2-31,23 = -0,0021435
ν7 = х1 + 80х2-32,26 = 0,001785
Вычисляем сумму:
![]() = 0,00016785714475
= 0,00016785714475
Среднеквадратичные отклонения результатов решения данной системы нормальных уравнений по формулам (7.15) равны:
![]() =
0,0058968195;
=
0,0058968195;
![]() =
0,0001095011
=
0,0001095011
Находим среднеквадратичные отклонения результатов:
![]() ;
;
![]() .
.
Отсюда надежные границы случайных ошибок по формулам (7.16):
![]()
![]() ;
;
![]()
![]() ;
;
где:
- коэффициент надежности
![]() (квантиль распределения Стьюдента) для
Р = 0,95 и (m –
n +1=6) равен
(квантиль распределения Стьюдента) для
Р = 0,95 и (m –
n +1=6) равен
![]() =2,571.
(см.
=2,571.
(см.
Результат измерения номинального сопротивления:
![]()
Результат косвенного измерения температурного коэффициента:
![]() ;
;
![]()
Окончательно,
результаты совместного измерения
номинального сопротивления и температурного
коэффициента при доверительной
вероятности
![]() :
:
R0
= (23,990![]() 0,015)
Ом;
0,015)
Ом;
α
= (0,004310![]() 0,000010)
K-1.
0,000010)
K-1.
По таблице значений температурных коэффициентов (см. приложение
ниже) можно сделать вывод, что катушка намотана медным проводом.
Значение
квантиля распределения Стьюдента для
6 степеней свободы
![]() =2,571.
=2,571.
Пример решения аналогичной задачи рассмотрен в [8], стр. 305 - 309.
Таблица 1.7. Значения температурных коэффициентов.
|
Материал |
, К-1 |
|
Медь |
0.0043 |
|
Железо |
0.0065 |
|
Алюминий |
0.0038 |
|
Константан |
0.0002 |
|
Нихром |
0.0001 |
|
Вольфрам |
0.0048 |
Варианты заданий (Rt, Ом)
|
Номер варианта |
T, °C |
||||||
|
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
110,78 84,76 62,03 129,14 81,46 94,19 146,34 115,25 67,31 102,03 150,60 72,78 79,12 161,41 75,72 102,08 81,16 135,57 70,04 87,95 91,52 137,71 75,03 70,14 106,02 152,80 76,01 |
115,15 89,61 62,04 133,66 84,67 94,29 151,52 121,85 70,00 102,06 155,90 75,63 83,64 167,08 80,05 106,12 81,24 140,35 74,08 91,45 96,76 146,61 75,04 70,21 112,30 158,20 79,04 |
119,54 94,51 62,05 138,21 87,91 94,36 156,65 128,54 72,65 102,08 161,30 78,51 88,21 172,81 84,41 110,18 81,32 145,14 78,13 94,92 102,08 147,42 75,05 70,28 118,40 163,60 82,05 |
123,92 99,37 62,06 142,81 91,11 94,47 161,84 135,16 75,35 102,10 166,70 81,42 92,74 178,51 88,76 114,21 81,41 149,92 82,16 98,45 107,31 152,31 75,07 70,36 124,50 168,90 82,03 |
128,32 104,26 62,07 147,35 94,36 94,97 167,02 141,76 78,00 102,12 171,90 84,28 97,30 184,18 93,12 118,25 81,48 154,75 86,17 101,91 112,57 157,15 75,10 70,40 130,60 174,40 88,06 |
132,71 109,11 62,08 151,93 97,57 94,65 172,15 148,43 80,62 102,14 177,20 87,18 101,84 189,90 97,49 122,28 81,57 159,51 90,22 105,35 107,85 162,01 75,11 70,48 136,70 179,80 91,07 |
137,09 114,00 62,09 156,48 100,80 94,76 177,32 155,01 83,32 102,16 182,60 90,05 106,42 195,01 101,82 126,35 81,65 164,30 94,23 108,84 123,15 166,92 75,12 70,57 142,8 185,2 94,08 |
