Потенциал электростатического поля

Работа консервативных сил осуществляется за счет уменьшения потен­циальной энергии.

Отсюда потенциальная энергия точечного заряда в поле заряда : 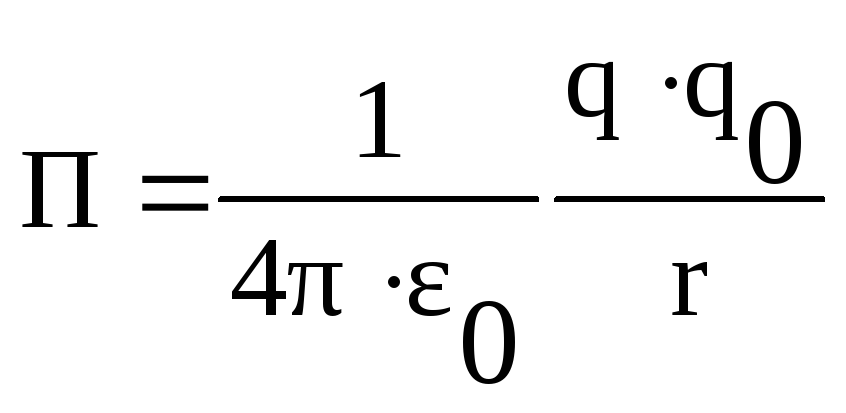, где - расстояние от заряда до заряда .

Потенциальная энергия одноименных зарядов положительна, а разноименных - отрицательна.

Если поле создается системой точечных зарядов , то по­тенциальная энергия заряда , находящегося в этом поле, равна алгебраической сумме потенциальных энергий, созданных каждым из зарядов в отдельности. Отношение не зависит от величины заряда и поэтому является энергетической характеристикой электростатического поля, называемой потен­циалом .

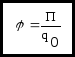
Потенциал поля, созданного точечным зарядом в вакууме:

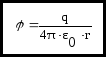
Следовательно, работа ;

Работа может быть также представлена как: . Отсюда . Интегрирование можно производить вдоль любой линии, соединяющей точки 1 и 2, так как работа не зависит от траектории перемещения.

Потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда из данной точки в бесконечность.

Размерность потенциала =1В (вольт)

Если поле создано несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов

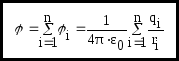
Напряженность как градиент потенциала

Вектор напряженности электрического поля может быть найден как градиент потенциала:

, где

- единичные векторы координатных осей . Знак (-) показывает, что вектор напряженности направлен в сторону убывания потенциала.

Эквипотенциальная поверхность — поверхность во всех точках который потенциал имеет одно и то же значение.

Линии напряженности (и вектор ) всегда нормальны (перпендикулярны) к экви­потенциальным поверхностям.

Вектор всегда направлен в сторону убывания потенциала.

Работа по перемещению заряда вдоль эквипо­тенциальной поверхности равна 0.

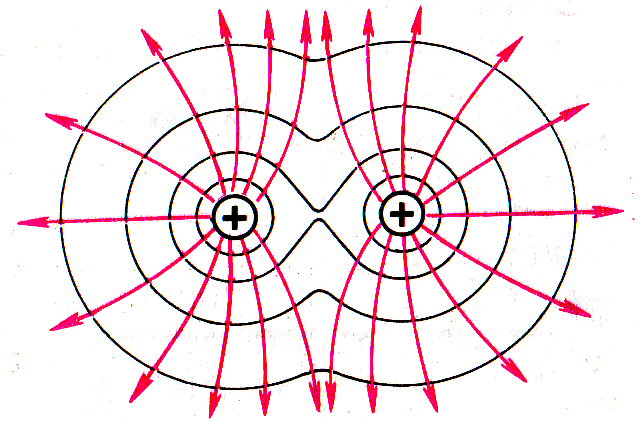
Рисунок 9. Силовые линии (напряженности) и эквипотенциальные поверхности, созданные двумя одноименными точечными зарядами

Н

апряженность электростатического поля Е между двумя эквипотенциальными поверхностями (Рисунок 10):

Рисунок 10. Эквипотенциальные поверхности

Разность потенциалов двух точек 1 и 2 определяется работой, со­вершаемой силами электростатического поля, при перемещении единич­ного положительного заряда из точки 1 в точку 2. .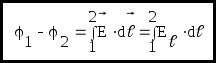

Интегрирование можно производить вдоль любой линии, соеди­няющей начальную и конечную точки, т.к. работа сил электростатическо­го поля не зависит от траектории перемещения.

Разность потенциалов некоторых полей

1) Поле равномерно заряженной бесконечной плоскости

Разность потенциалов между точками, лежащими на расстоянии х₁ и х₂ от плоскости равна:

2) Поле двух бесконечных параллельных разноименно заряженных плоскостей d – расстояние между пластинами

3) Поле равномерно заряженной сферической поверхности

Разность потенциалов между точками, лежащими на расстоянии r₁ и r₂ от центра сферы (r₁R, r₂R):

Внутри сферической поверхности потенциал всюду одинаков и равен:

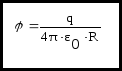
4) Поле объемно заряженного шара радиусом R с общим зарядом q .

Вне шара: , поэтому

Между двумя любыми точками внутри шара на расстоянии r' R от его центра:

5) Поле равномерно заряженного бесконечного цилиндра (нити) радиусом R с линейной плотностью .

Вне цилиндра (r  R) .

Разность потенциалов:

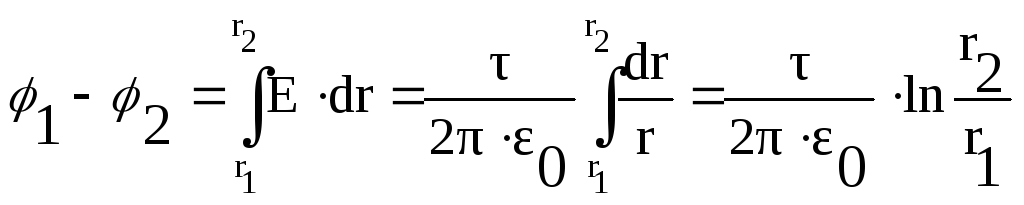
Контрольные вопросы

1. Расскажите о работе по перемещению заряда в электрическом поле?

1. Чему равна потенциальная энергия точечного заряда, помещенного в электрическое поле?

2. Что Вы знаете о потенциале электрического поля?

3. Что такое эквипотенциальная поверхность и как относительно нее направлены векторы напряженности электрического поля?

4. Чему равна работа по перемещению заряда вдоль эквипотенциальной поверхности?