5. Операції над графами

За допомогою різних операцій можна будувати графи з більш простих, переходити від одного графа до іншого, більш простого, розбивати граф на більш прості, у заданому класі графів переходити від одного графа до іншого і т.д.

Найбільш вживаними одномісними операціями є:

1. Операція вилучення вершини з графа , що полягає у вилученні деякої вершини разом з інцидентнимі їй ребрами.

2. Операція вилучення ребра з графа полягає у вилученні відповідної пари з E. При цьому усі вершини зберігаються.

3. Операція додавання вершини до графа . Додану вершину можна з'єднати ребрами з деякими вершинами графа .

4. Операція додавання ребра до графа між двома вершинами.

Вилучаючи ребро і додаючи нову вершину, що з'єднується ребром з кожною вершиною вилученого ребра, робимо операцію підрозділу ребра графа .

Приклад.

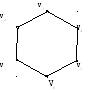
G₁=(V₁, E₁)

G₂=(V₂, E₂)

V₂=V₁ V {V₆}

E₂=(E₁‏\{(V₁,V₅)})U{(V₁,V₆);

(V₆,V₅)}

G₂

Означення.Граф G₂ називається підрозділом графа G₁, якщо він може бути отриманий з G₁ шляхом застосування кінцевого числа операцій підрозділу ребер.

Найбільш уживаними 2-місними операціями над графами є об'єднання і декартовий добуток.

Означення. Нехай G₁=(V₁,E₁); G₂=(V₂,E₂) – два графи таких, що V₁∩V₂=Ø, E₁∩E₂=Ø. Об'єднанням графів і називається граф з множиною вершин V=V₁UV₂ і множиною ребер E₁UE₂

Приклад.

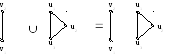
Нехай задані графи і з множинами вершин і .

Означення. Декартовим добутком графів і називається граф , множиною вершин якого є елементи декартового добутку множин і , причому дві з цих вершин і суміжні тоді і тільки тоді, коли або і вершина суміжна з вершиною , або і вершина суміжна з вершиною .

Приклад.

=

6. Види графів

1. Тривіальні і повні графи.

Означення. Граф, що складається з однієї вершини, називається тривіальним.

Означення. Граф, що має максимально можливе число ребер називається повним.

2) Дерево і ліс.

Означення. Деревом називається зв'язний ациклічний неорієнтований граф, Дерево не містить петель і кратних ребер.

Приклад.

Властивості дерев.

1. Щоб простий зв'язний граф був деревом, необхідно й достатньо, щоб число вершин було більше числа ребер на одиницю.

2. Щоб граф був деревом, необхідно й достатньо, щоб будь-які дві його вершини з'єднувалися єдиним маршрутом.

3. Граф буде деревом тоді й тільки тоді, коли додавання будь-якого нового ребра приводить до появи рівно одного циклу.

Означення. Остовним деревом для графа називається остовний підграф, який є деревом.

Означення. Лісом називається незв'язний неорієнтований граф без циклів, в якому кожна зв'язна компонента є деревом.

Будь-яка частина дерева або ліса також є деревом або лісом. Будь-який ланцюг у такому графі простий (інакше він містив би цикл).

3) Дерево з коренем.

Виділимо в дереві вершину . Цю вершину називають коренем дерева , а саме дерево називають деревом з коренем. У дереві з коренем можна природним чином орієнтувати ребра. Вершину ребра можна з'єднати єдиним ланцюгом з коренем . Якщо цей ланцюг не містить ребра , то вводиться орієнтація від к , в противному випадку – від до . Орієнтоване в такий спосіб дерево з коренем називається орієнтованим деревом. У ньому всі ребра мають напрямок від кореня:

У кожну вершину орієнтованого дерева (за винятком ) входить тільки одне ребро, тобто, ця вершина є кінцем одного і тільки одного ребра. У корінь не входить жодне ребро, усі інцидентні кореню ребра зв'язують його зі своїми другими кінцями, виходить, є їхнім початком.

Будь-яке дерево можна орієнтувати, вибравши як корінь будь-яку його вершину.