6. Досяжність і зв’язність. Компоненти зв’язності.

Означення. Граф G називається зв'язним, якщо будь-яка пара його вершин з'єднана маршрутом.

Теорема (про число маршрутів, які з’єднують будь-яку пару вершин графа). Нехай - матриця суміжності графа і . Тоді є число маршрутів довжини від до .

Наслідок 1. Маршрут від вершини до вершини () в графі існує тоді і тільки тоді, коли ()-й елемент матриці не дорівнює нулю.

Наслідок 2. Маршрут від вершини до вершини в графі існує тоді і тільки тоді, коли ()-й елемент матриці не дорівнює нулю.

Означення. Нехай – деяка матриця. Булевим відображенням для матриці називається відображення

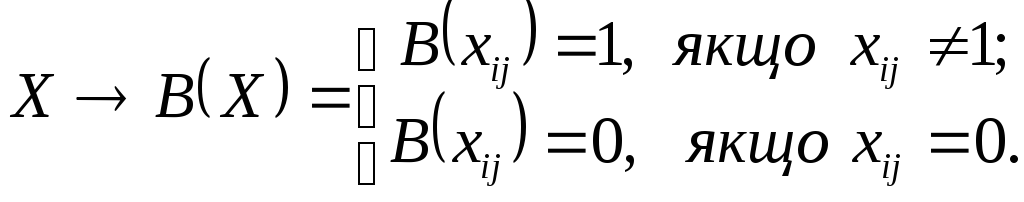
Означення. Матрицею досяжності графа називається матриця

де – число вершин, – одинична матриця, – булево відображення.

Маршрут від вершини до вершини існує в графі тоді й тільки тоді, коли дорівнює 1.

Граф є зв’язним тоді й тільки тоді, коли для всіх (матриця досяжності заповнена одиницями).

Властивість зв'язности можна розглянути як бінарне відношення, яке:

а) рефлексивне: вершина зв'язана сама із собою;

б) симетричне: якщо вершина зв'язана з вершиною , то й вершина зв'язана з вершиною

в) транзитивне: якщо вершина зв'язана з вершиною , і зв'язана з вершиною , то вершина зв'язана з вершиною .

Відношення зв’язності є відношенням еквівалентності, тобто воно розбиває множину вершин графа на класи, які попарно не перерізаються. Оскільки кожна множина - множина зв'язаних вершин, а вершини з різних множин не зв'язані, то маємо розкладання графа G на частини, які не перерізаються і кожна частина - зв'язна.

Означення. Нехай - розбиття графа , обумовлене відношенням зв’язності. Число називається числом зв’язності графа .

Означення. Компонентами зв’язності графа називаються підграфи графа, породжені класами еквівалентності.

Компоненти графа визначаються за його матрицею досяжності: якщо вона має блочно-діагональний вигляд, то кожен блок визначає одну компоненту зв’язності. Якщо піднести матрицю досяжності до квадрату, то елемент визначає число елементів в тій компоненті, в яку входить вершина .

Означення. Орграф називається зв’язним, якщо існують шляхи для всіх пар різних вершин графа.

Матриця досяжності визначається аналогично графам. Але відзначимо, що для орграфів відношення зв’язності не є відношенням еквівалентності на множині вершин і, отже, не здійснює розбиття множини .

Для орграфів поняття зв’язності є більше змістовним, чим для неорієнтованих графів. Розрізняють три важливих типи зв’язності орграфа:

а) орграф сильно зв'язний, якщо для кожної пари різних вершин , з існує шлях (орієнтований ланцюг) з в і з в .

б) орграф односторонньо зв'язний, якщо для кожної пари різних вершин , з існує шлях з в або з в .

в) орграф слабко зв'язний, якщо граф, отриманий з скасуванням орієнтації є зв’язним.

Очевидно, що справедливі наслідки:

G сильно зв'язний G односторонньо зв'язний G слабко зв'язний.

Приклад.

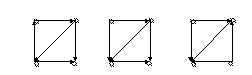
Сильна, одностороння і слаба зв'язність.

У термінах матриці зв’язності орграф G сильно зв'язний тоді і тільки тоді, коли для всіх ; G односторонньо зв'язний тоді й тільки тоді, коли або для всіх .

Твердження. Орграф є сильно зв'язний тоді й тільки тоді, коли в ньому є остовний циклічний маршрут.

Означення. Компонентами сильної зв’язності орграфа називаються його максимальні сильно зв'язні підграфи.

Кожна вершина орграфа належить тільки одній компоненті сильної зв’язності. Якщо вершина не зв’язана з іншими, то вважають, що вона сама утворює компоненту сильної зв’язності.

Означення. Конденсацією орграфа (або фактор-графом) називається орграф, який отриманий стягуванням в одну вершину кожної компоненти сильної зв’язності орграфа .

Приклад орграфа ті його конденсації: