23

Розділ 3

Елементи теорії графів.

Елементи теорії алгоритмів.

Тема 4. Елементи теорії графів

1. Означення графа. Зображення графів

Означення. Графом (скінченим графом) називається сукупність двох множин – скінченої множини і множини пар елементів з . Елементи множини називаються вершинами графа, а елементи множини – його ребрами.

Приклад 1. Нехай ,

. Тоді множини і визначають граф .

Будь-який граф визначається відношенням інцидентності між множинами вершин і ребер . Якщо вершина є кінцем ребра , то кажуть, що інцидентна . Відношення інцидентности є узагальненням відношення належності, воно нерефлексивне і симетричне. Зауважимо, що кожен елемент інцидентний рівно двом елементам і з .

Означення. Два ребра, інцидентні одній вершині, називаються суміжними; дві вершини, інцидентні одному ребру , також називаються суміжними.

Часто розглядають наступні поріднені до графів об’єкти.

Означення. Якщо елементами множини є впорядковані пари, то граф називається орієнтованим (або орграфом). В цьому випадку елементи множини називаються вузлами, а елементи множини - дугами. В орієнтованім графі перша за порядком вершина, інцидентна ребру, називається його початком, друга – його кінцем.

Означення. Якщо елементом множини є пара однакових елементів множини , то такий елемент множини називається петлею, а граф називається графом з петлями (або псевдографом).

Означення. Якщо є не множиною, а набором, який містить декілька однакових елементів, то ці елементи називаються кратними ребрами, а граф називається мультиграфом.

Приклад 2. Нехай ,

. Тоді - граф (мультиграф), - петля, - кратне ребро.

Введене поняття графа є абстрактним.

Розглянемо в евклідовому просторі фігури певного вигляду. Кожна з таких фігур складається з різних вершин і кривих, кожна з яких з'єднує деякі пари вершин (можливе виродження ). Криві можуть бути дугами кіл чи відрізками прямих. Припустимо також, що ніяка внутрішня точка кривої фігури не є вершиною чи внутрішньою точкою іншої кривої.

Означення. Фігура називається геометричним зображенням графа G , якщо існує взаємно однозначна відповідність між вершинами фігури и вершинами графа , а також між кривими фігури и ребрами графа така, що якщо , то (відповідні криві і ребра з'єднують відповідні вершини).

Приклад 3. Наступні фігурі є геометричним зображенням графів з прикладів 1 і 2.

Приклад 1. Приклад 2.

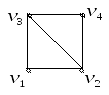
- ізольована вершина; , - кінцеві вершини$

ребро - петля, ребро - кратне ребро.

Теорема. (Про геометричне зображення скінченного графа). Будь-який скінченний граф може бути зображений у 3-вимірному евклідовому просторі.

При зображенні орграфів напрямки ребер зображаються стрілками, які примикають до їх кінців. Орграф може мати петлі, кратні ребра,а також ребра, які з’єднують одні й ті самі вершини, але йдуть в протилежних напрямках.

Приклад 4.

2. Способи завдання графа: матрицею інцидентності, списком ребер, матрицею суміжності.

Граф вважається заданим, якщо визначені множини його вершин і ребер, а також відношення інцидентності. Для визначення вершин і ребер скінченого графа їх достатньо занумерувати. Нехай - вершини графа , - його ребра.

Розглянемо наступні способи завдання графа :

а) Завдання графа матрицею інцидентності.

Означення. Матрицею інцидентності графа називається - матриця , де

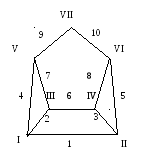
Приклад 5.

вешини ребра	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ	Ⅶ
1	1	1	0	0	0	0	0
2	1	0	1	0	0	0	0
3	0	1	0	1	0	0	0
4	1	0	0	0	1	0	0
5	0	1	0	0	0	1	0
6	0	0	1	1	0	0	0
7	0	0	1	0	1	0	0
8	0	0	0	1	0	1	0
9	0	0	0	0	1	0	1
10	0	0	0	0	0	1	1

Означення. Матрицею іинцидентності орграфа називається - матриця , де

Приклад 6.

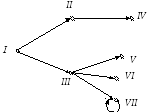
вершини ребра	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ	Ⅶ
1	-1	1	0	0	0	0	0
2	-1	0	1	0	0	0	0
3	0	-1	0	1	0	0	0
4	0	1	0	-1	0	0	0
5	0	0	-1	0	1	0	0
6	0	0	-1	0	0	1	0
7	0	0	-1	0	0	0	1
8	0	0	0	1	0	1	2

³

1 ₄

₅

2 ⁶

₇

⁸

У кожнім рядку матриці інцидентності для неорієнтованого або орієнтованого графа тільки два елементи не дорівнюють 0 (або один, якщо ребро є петлею ). Тому такий спосіб завдання недостатньо ощадливий.

б). Завдання графа списком ребер.

Означення. Списком ребер графа називається таблиця, у кожнім рядку якої, що відповідає ребру, записані номери вершин, інцидентних йому. Для неорієнтованого графа порядок вершин у рядку довільний, для орієнтованого графа першим стоїть номер початку ребра, другим – номер кінця.

Приклад 7. Задамо списком ребер граф із приклада 5.

Ребра	Вершини
1	I, II
2	I, III
3	II, IV
4	I, V
5	II, VI
6	III, IV
7	III, V
8	IV, VI
9	V, VII
10	VI, VII

Приклад 8. Задамо списком ребер граф із приклада 6.

Ребра	Вершини
1	I, II
2	I, III
3	II, IV
4	IV, II
5	III, V
6	III, VI
7	III, VIII
8	VII, VII

За списком ребер графа легко побудувати його матрицю інцидентності. Дійсно, кожен рядок цього списку відповідає рядку матриці з тим же номером. Для неорієнтованого графа в рядку списку зазначені номери елементів рядка матриці інцидентності, які дорівнюють 1, і для орієнтованого графа в цьому рядку першим стоїть номер елемента рядка матриці, який дорівнює –1, а другим - номер елемента рядка,який дорівнює +1.

в) Завдання графа матрицею суміжності.

Означення. Матрицею суміжності графа називається квадратна – матриця , стовпцям і рядкам якої відповідають вершини графа. Для неорієнтованого графа - число ребер, іинцидентних -й і-й вершинам. Для орієнтованого графа - число ребер з початком у-й і кінцем у-й вершині.

Приклад 9. Задамо матрицею суміжності граф із приклада 5.

I II III IV V VI VII

I 0 1 1 0 1 0 0

II 1 0 0 1 0 1 0

III 1 0 0 1 1 0 0

IV 0 1 1 0 0 1 0

V 1 0 1 0 0 0 1

VI 0 1 0 1 0 0 1

VII 0 0 0 0 1 1 0

Приклад 10. Задамо матрицею суміжності граф із приклада 6.

I II III IV V VI VII

I 0 1 1 0 0 0 0

II 0 0 0 1 0 0 0

III 0 0 0 0 1 1 1

IV 0 1 0 0 0 0 0

V 0 0 0 0 0 0 0

VI 0 0 0 0 0 0 0

VII 0 0 0 0 0 0 1

Матриця суміжності неорієнтованого графа симетрична (тобто ), а орієнтованого - не обов'язково.

Для неорієнтованого графа всі його ребра визначаються верхнім правим трикутником матриці, розташованим над головною діагоналлю, включаючи останню. Кількість ребер дорівнює сумі по цьому трикутнику, тобто . Ребра орієнтованого графа визначаються всіма елементами матриці суміжності.