1.Проектировачный расчет.

1.1. Выбираем сечение ремня по рис. 2.57.

Получаем ремень типа Б, у которого размеры сечения в_р=14мм. в_о=17мм. h=9.5мм. А₁=138 мм².

А₁

в_о

h

1.2. По табл. 2.27 для выбранного сечения ремня Б принимаем диаметр меньшего шкива d₁=125 мм.

1.3. Диаметр большого шкива с учётом ε=0.01(к-т скольжения в передаче).

d₂= d₁*U(1- ε) = 125*4.5(1-0.01) = 556.8 мм.

Принимаем d₂₌560мм. из стандартного ряда п. 4.10.

1.4. Фактическое передаточное число U_ф:

U_ф= 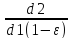= = 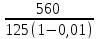4.52

Отклонения ∆U= 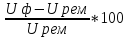≤ 5

∆U=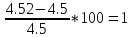

1.5. Ориентировочное межосевое расстояние а, мм.

а ≥ 0.55 (d₁+d₂)+h = 0.55 (125+560) +9.5 = 386.25мм.

Округляем в большую сторону до целого числа.

а=387 мм.

1.6. Определяем длину ремня.

L_p= 2а +0.5 π (d₁+d₂)+ 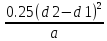=2*387 +0.5*3.14(125+560) + 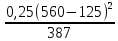= 1971,65мм.

По табл.2.27 принимаем L_p=2000 мм.

1.7. Фактическое межосевое расстояние, а мм.

A=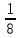[2L_p-π(d₂+d₁)+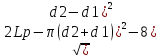]= =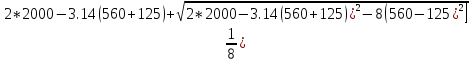403.68 мм.

1.8. Угол обхвата ремнём меньшего шкива.

α₁ =180°-57° 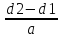= 180°-57° 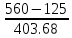=121°

>[α₁] =120

1.9. Скорость ремня, Ѵ

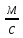
Ѵ= 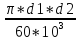= = 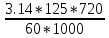4.71

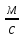
<[Ѵ]= 25

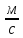
1.10. Частота пробега ремня U

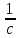
U=

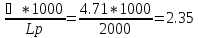
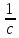
<[U]= 10÷20 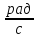, что гарантирует долговечность в пределах 2000÷3000 часов.

1.11. Определяем мощность, передаваемую одним ремнём в условиях эксплуатации Р , кВт.

[P] = 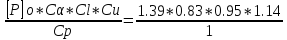= 1.24 кВт.

Где P_o- номинальная мощность, кВт. (т.2.28) P_o= 1.39 кВт.

C_α –к-т. угла обхвата на меньшем шкиве.C_α= 0.83

C_L- к-т., учитывающий влияние длины ремня L к базовой(эталоновой) L_o= 2240

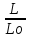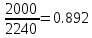=, C_L= 0.95 (т.2.33)

C_u-к-т. передаточного числа C_u= 1.14 при U_рем=4.5 (т.2.31)

C_p- к-т. динамической нагрузки C_p=1 (т.2.30)

1.12. Число ремней в комплекте.

Z=

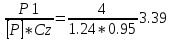
Принимаем Z=3

<[Z]=10

Где Р₁- мощность на I валу = 4 кВт.

С_z – к-т., учитывающий неравномерность нагрузки ремней (стр.128)

С_Z = 0.95.

1.13. Сила предварительного натяжения ремня F_о , Н:

F_o = 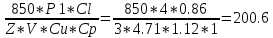Н.

1.14.Окружная сила F_t ,Н:

F_t = 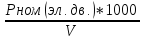= 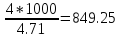Н.

1.15.Сила натяжения вщ. F₁ и вм. F₂ ветвей, Н.

F₁ = F_o+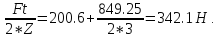

F₂= F_o-

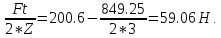
1.16. Cила давления ремня на вал.

F_вал.= F_o*Z*sin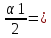200.6*3*sin74° = 523.5 Н.

V этап. Расчет конической передачи.

Дано:1.Вращающий момент

На ведущем валу.

М₁=Т₂=99.7 Н*м.

2.Частота вращения ведущего

Вала.n₂=160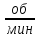

(ω₂=37.68)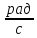

3. Передаточное число редуктора.

U_ред=2.

Решение:

1. Вращающий момент на ведомом валу редуктора:

М₂ = М₁* U = 99.7*2 = 199.4 Н*м

2. Материалы зубчатых колёс. По табл.9.2 для шестерни и колеса принимаем сталь 35ХМ. Вид ТО-улучшение с закалкой ТВЧ до твёрдости поверхности зубьев 49…65 HRC, G_T = 750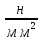 , при предполагаемом диаметре заготовки шестерни D < 200 мм. и ширине заготовки колеса S≤ 125мм.

Принимаем значение твёрдости зубьев 54HRC.

3. Допускаемое контактное напряжение определяем по формуле (9.37)

[G_H] = (δ_HO/[S_H])*K_HL

Для материала зубьев шестерни и колеса принимаем закалку при нагреве ТВЧ по всему контуру зубьев.

δ_HO= 17HRC + 200 (T.9.3)

[S_H]=1.2(при закалке) K_HL=1 (§9,11)

Допускаемый к-т. к-т. долговечности, учит.

Безопасности режим нагрузки передачи.

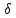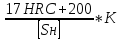[_H]=_HL=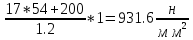

4. Допускаемое напряжение изгиба по формуле 9.42.

[G_F]=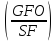*K_FC*K_FL=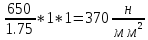

По табл. 9.3. G_FO= 650 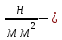предел выносливости зуба при изгибе.

[S_F]- допускаемый к-т. безопасности

[S_F] =1.75 для зубчатых колес, изготовленных из поковок и штамповок.

K_FC =1-к-т., учитывающий влияние приложения нагрузки.

K_FL =1-к-т. долговечности (при длительно работающей передаче).

5. К-т. ширины зубчатого венца (9.77.)

Ψ_d=0.166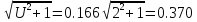

6. По табл. 9.5 принимаем к-т. неравномерности распределения нагрузки по ширине зубчатого венца K_Hβ=1.3 (при симметрич. располож.)

7. Внешний делительный диаметр колеса определяем по ф-ле. 9.73.

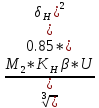d_e2= 165 = 165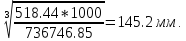

Принимаем стандартное значение и ширину зубчатого венца:

d_e2=160 мм.

b= 25 (т.9.7)

8. Расчётные коэффициенты (т.9.5)

V_F= 0.85 –к-т. вида конических колёс.(для прямозубых =0.85)

при Ψ_d = 0.370 к-т. K_Fβ = 1.6

9. Внешний окружной модуль по ф-ле. 9.79.

m_e ≥ 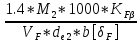= = 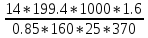3.55мм.

10. Число зубьев колеса и шестерни.

Z₂ = =

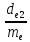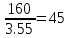
Z₁ = =

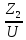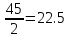
Принимаем:

Z₁ = 23

Z₂ = 45

11. Фактическое передаточное число.

U_ф = =

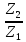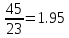
Отклонение _∆U= = =

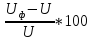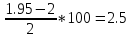
12. Углы делительных конусов по ф-ле.:

tg б₂ =U_ф =1.95 б₂ = 62°54̒

б₁ = 90 - 62°54̒ = 89°60̒ - 62°54̒ = 27˚6̒

13. Основные геометрические размеры (ф.9.50-4.)

d_e1 =m_e*Z₁ = 3.55*23= 80.5

R_e= 0.5 m_e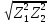 = 0.5*3.55* 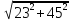= 89.6

R= R_e – 0.5b = 89.6 – 0.5*25 =77.1мм.

m= =

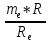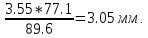
d₁₌ m*Z₁ = 3.05*23 = 70.15мм.

d₂₌ m*Z₂ = 3.05*45 = 137.25мм.

d_ae1= d_e1+ 2m_e cos б1 = 80.5+2*3.55*0.8902 = 86.82

d_ae2= d_e2+ 2m_e cos б2 = 160+2*3.55*0.4555 = 163.23

14. Средняя окружная скорость колёс.

Ѵ = 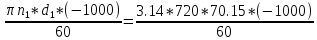= 2.64 м/с.

по т.9.1. принимаем 9 степень точности.

15. Силы в зацеплении.

F_t­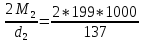 = = 2905 H.

Радиальная на шестерне и осевая на колесе.

F_r1 =F_a2 = F_t * tg a_w * cos б₁ = 2905*tg20˚ * cos 27˚6̒ = 941.23 H.

Осевая на шестерне и радиальная на колесе.

F_a1 =F_r2 = F_t * tg a_w * cos б₁ = 2905*0.36 * 0.45 = 470.61 H.

16. К-т. динамической нагрузки K_HV= 1.1 (см. т.9.6.), К_Нβ =1,3 (не симметрическом расположении колёс.)

17. Расчетное контактное напряжение по ф-ле. 9.74.

G_H = 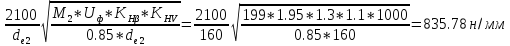².

Контактная прочность зубьев обеспечивается, т.к. 835 н/мм² меньше допускаемого [G_H] = 930 н/мм².

18. Эквивалентное число зубьев шестерни и колеса по ф-ле. 9.46.

Z_v1 =

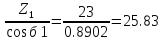
Z_v2=

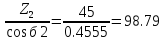
К-т. формы зуба.

Y_F1 =4

Y_F2 = 3.6

19. Принимаем к-ты.

K_FV = 1.2 (т.9.6.)

K_Fβ = 1.5

20. Расчетное напряжение изгиба в основании зубьев шестерни по ф-ле. 9.78.

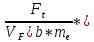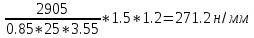G_F1 = Y_{F1 *} K_{Fβ *} K_{FV =} 4².

277.2 < [G_F] = 370н/мм² т.е. прочность обеспечивается.