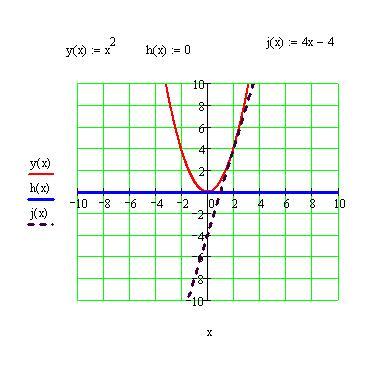
9 Билет: геометрический смысл производной. Уравнение касательной к графику функции.

Уравнение Касательной Касательной к графику функции называется предельное положение секущей при стремлении точки М к точке М₀ вдоль графика.

Геометрический смысл производной.

Пусть L – некоторая кривая, M₀– точка на кривой L .

Любая прямая, пересекающая L не менее чем в двух точках называется секущей.

Касательной к кривой L в точке M₀ называется предельное положение секущей, если точка стремится к, двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке он имеет невертикальную касательную . Ее уравнение: (уравнение прямой, проходящей через точкуи имеющую угловой коэффициент k).По определению углового коэффициента, где – угол наклона прямой к оси. Пусть – угол наклона секущейк оси, где . Так как – касательная, то при . Следовательно,

10 билет: производная суммы и производная частного

11 билет: производная основных элементарных функций

12 билет: производная тригонометрических функций

, , ,

, ,

13 билет: первообразная. неопределенный интеграл. его свойства

Первообразной функции f на промежутке I называется функция F, такая, что

Неопределенный интеграл где F - первообразная функции f (на промежутке); C - произвольная постоянная.

Основные свойства

1. 

2. 

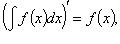
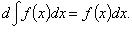
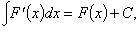
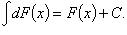
3. Если 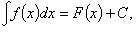то

4. 

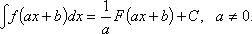
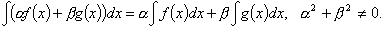
14 билет: определенный интеграл, его свойства

Определенным интегралом функции y=f(x) заданной на отрезке [a;b] называется предел интегральной суммы сигма при лямде, стремящейся к 0, если этот предел существует и конечен.

Свойства определенного интеграла:

1)2)3)4)

5)

15 билет: геометрический смысл определенного интеграла

Площадь криволинейной трапеции

Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции. 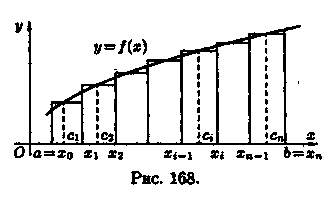Для этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х0<x1<...<xn) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).Умножим значением функции ƒ(ci) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max∆xi →0: Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.