
- •Первообразная. Неопределенный интеграл и его свойства.
- •Интегрирование заменой переменной.
- •Определение рациональной функции. Разложение правильной рациональной дроби на сумму простейших дробей.
- •Интегрирование простейших дробей первого и второго типов.
- •Интегрирование дробей вида и .
- •Интегрирование иррациональных функций вида
- •Интегрирование иррациональных функций. Первая подстановка Эйлера.
- •Интегрирование иррациональных функций. Вторая подстановка Эйлера.
- •Определенный интеграл. Определение. Физический и геометрический смысл.
- •Свойства определенного интеграла. Теорема о среднем.
- •Производная интеграла с переменным верхним пределом.
- •Абсолютно сходящиеся интегралы первого рода. Теоремы о сходимости.
- •Несобственные интегралы второго рода. Теоремы сравнения.
- •Абсолютно сходящиеся интегралы второго рода. Теоремы о сходимости.
- •Непрерывность функции нескольких переменных
- •27. Частные производные. Геометрический смысл частных производных функции двух переменных.
- •28. Дифференцируемость функции нескольких переменных.
- •29. Необходимые условия дифференцируемости функции. Достаточное условие.
- •30. Полные дифференциалы. Частные дифференциалы.
- •31. Производные сложных функций.(правильное)
- •32. Неявные функции. Теорема о существовании неявной функции.
- •33. Касательная плоскость и нормаль к поверхности.
- •34. Производные высших порядков.
- •35. Дифференциалы высших порядков.
- •37. Экстремум функции нескольких переменных. Необходимое условие существования экстремума.
- •38. Достаточное условие экстремума функции двух переменных.
- •39. Условный экстремум.
- •40. Производная поля по направлению. Градиент функции.
- •41. Двойной интеграл. Определение и основные свойства.
- •42. Сведение двойного интеграла к повторному (случай прямоугольника).
- •43. Сведение двойного интеграла к повторному (случай произвольной области).
- •46. Двойной интеграл в полярных координатах.
- •47. Тройной интеграл. Свойства тройных интегралов.
- •48. Вычисление тройного интеграла в декартовых координатах.
- •49. Вычисление тройного интеграла в цилиндрических координатах.
- •50. Вычисление тройного интеграла в сферических координатах.
- •51. Криволинейные интегралы первого рода. Определение. Свойства. Вычисления.
- •52. Криволинейные интегралы второго рода. Вычисления.
- •53. Формула Грина.
- •54. Поток вектора через поверхность. Его свойства.
- •55. Поток вектора через незамкнутую поверхность
- •56. Поток вектора через замкнутую поверхность. Теорема Гауса-Остроградского.
- •57. Дивергенция векторного поля.
- •58. Циркуляция векторного поля. Ротор вектора.
39. Условный экстремум.
40. Производная поля по направлению. Градиент функции.
Производной
функции
![]() в
точке
в
точке
![]() по направлению
по направлению
![]() называется предел
называется предел
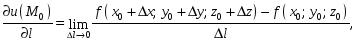
![]()
если предел существует.
Если функция
![]() дифференцируема в точке М0, то производная
по направлению вычисляется по формуле
дифференцируема в точке М0, то производная
по направлению вычисляется по формуле
!!!![]() (18.31)
(18.31)
В частности, если
![]() – функция двух переменных, то формула
(18.31) производной по направлению примет
вид:
– функция двух переменных, то формула
(18.31) производной по направлению примет
вид:
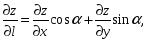 (18.32)
(18.32)
!!!где
![]() – угол между вектором
– угол между вектором
![]() и осью Ох.
и осью Ох.
Градиентом
функции
![]() в точке
в точке
![]() называется вектор, имеющий координаты:
называется вектор, имеющий координаты:
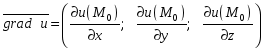 (18.33)
(18.33)
или, то же самое,
!!!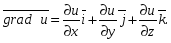
Связь между градиентом функции и производной по направлению устанавливает формула
![]()
где
![]() – угол между векторами
– угол между векторами
![]() и
и
![]()
Градиент функции
указывает направление наибыстрейшего
возрастания функции. Наибольшее значение
производной
![]() достигаемое в направление градиента,
равно
достигаемое в направление градиента,
равно

В
частности, если
![]() – функция двух переменных, то
– функция двух переменных, то

41. Двойной интеграл. Определение и основные свойства.
Пусть в замкнутой
ограниченной области D
плоскости xOy
определена
непрерывная функция
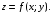 Разобьем указанную область произвольным
образом на элементарные плоские области
Разобьем указанную область произвольным
образом на элементарные плоские области
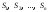 (рис. 24.1), площади которых будем считать
соответственно равными
(рис. 24.1), площади которых будем считать
соответственно равными
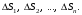 Внутри каждой элементарной области
выберем произвольную точку
Внутри каждой элементарной области
выберем произвольную точку
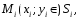
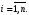
Достаточное условие интегрируемости функции: если определенная в некоторой ограниченной замкнутой области функция непрерывна, то она интегрируема в этой области.
Если функции
f(x; y),
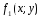 и
и
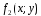 интегрируемы в области D,
то имеют место следующие свойства:
интегрируемы в области D,
то имеют место следующие свойства:
1) линейность:

где

2) аддитивность:
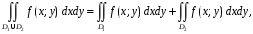
причем области
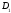 и
и
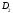 не имеют общих внутренних точек;
не имеют общих внутренних точек;
3) если
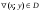 выполняется неравенство
выполняется неравенство
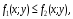 то
то

4) оценка модуля интеграла:
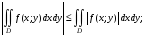
5) если
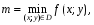
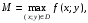 то
то
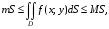
где S – площадь области D.
42. Сведение двойного интеграла к повторному (случай прямоугольника).
D – прямоугольник.
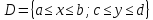
Проведём
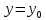 ;
;
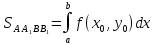 ;
;
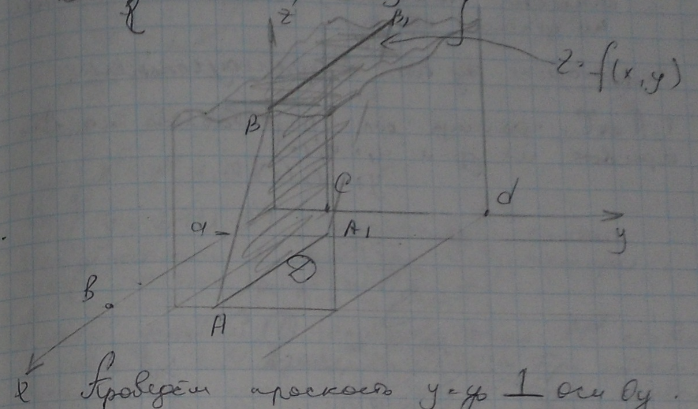
Проведём
плоскость, перпендикулярную оси Oy:
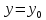 ;
;
Эта
плоскость пересечёт тело по криволинейной
трапеции
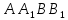 .
Её площадь:
.
Её площадь:
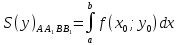 ;
;
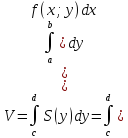 ;
;
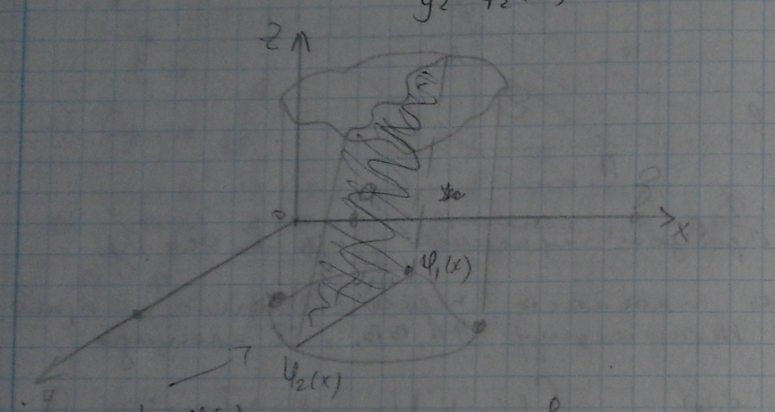
43. Сведение двойного интеграла к повторному (случай произвольной области).
Предположим, что область удовлетворяет условию:
-
Любая прямая || OY пересекает границу области не более, чем в двух точках либо по целому отрезку.
Проведём
плоскость, перпендикулярную оси Oy:
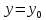 ;
;
Тогда граница области разбивается на две кривые, уравнения которых:
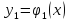 ;
;
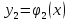 ;
;
Тогда:
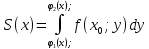 ;
;
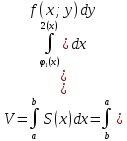 ;
;
 !!!44.
Замена переменных в двойном интеграле.
!!!44.
Замена переменных в двойном интеграле.
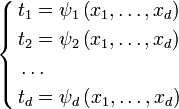
где t — «старые» координаты, а x — «новые» координаты. Пусть также функции, задающие отображение, имеют в области
![]()
![]() непрерывные частные
производные первого порядка и отличный
от нуля Якобиан
непрерывные частные
производные первого порядка и отличный
от нуля Якобиан

!!!45. Якобиан и его геометрический смысл.
Якобиа́н (определитель Яко́би, функциональный определитель) — определитель матрицы Якоби:
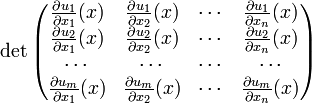
для
векторной функции
![]()
имеющей
в некоторой точке x все частные производные
первого порядка (определитель Якоби
или якобиан системы функций
![]() ).
).
Часто используются следующие обозначения якобиана:
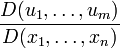 или
или
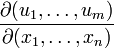
Определитель Якоби обычно определён для случая m = n, то есть для квадратных матриц Якоби; для m ≠ n его можно считать нулём (в простейшей интерпретации матрица Якоби дописывается при этом нулями до квадратной).

