-
Абсолютно сходящиеся интегралы первого рода. Теоремы о сходимости.
Пусть ф-я f(x) определена для всех x>=a, и интегрируема на [a,b].
Несобственный
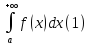наз. абсолютно сходящимся, если сходится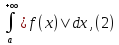
Если (1) сходится, а (2) расходится, то (1) условно сходящийся.
Если (2) сходится, то сходится (1)
Теорема:
Если
существует
,
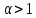что для любого достаточно большого x
ф-я f(x)
удовлетворяет условию:
,
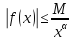то (1) сходится абсолютно.
-
Несобственные интегралы второго рода. Теоремы сравнения.
Пусть
ф-я f(x)
интегрируема на [a,
b-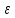
]
при
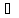сколь угодно малом
,
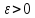но неограничена в интервале (b-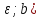
.
Определим, что мы будем понимать под
символом:
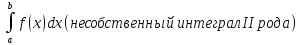
Рассмотрим
ф-ю I(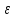
)
=
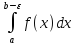
Если
при
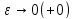ф-я I(
)
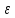имеет конечный предел, то несобственный
интеграл сходится и по определению он
равен:
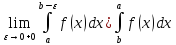
Аналогично
если ф-я f(x)
неограниченна только в интервале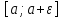
несобственный интеграл 2-го рода
определяется так:
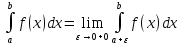
Теоремы сравнения:
-
Пусть f(x) и
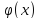интегрируемы на [a,b-
]
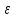и для них выполняется условие
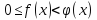, x
.
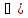Тогда:
-
Если сходится
-
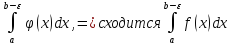
Если расходится
=>
-
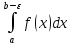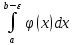
Пусть положительные на [a,b] ф-и f(x) и
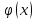– терпят разрыв в т. b,
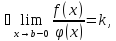тогда:
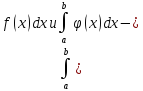сходятся
или расходятся одновременно.
-
Абсолютно сходящиеся интегралы второго рода. Теоремы о сходимости.
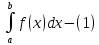называется
Абсолютно сходящимся если сходится
/
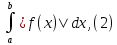Теорема: Если сходится (2), то сх. (1).
Теорема:
Пусть
f(x)
неограниченна только в (b-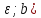
.
Если
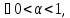для
всех x,
близких и < b
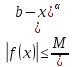
То
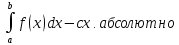
Главное значение интеграла 2-го рода.
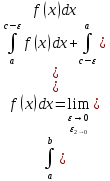
Говорят,
что несобственный
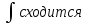в смысле главного значения, если
-
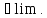
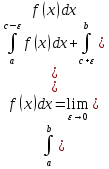
Понятие функции нескольких переменных. Предел функции нескольких переменных.
-
Непрерывность функции нескольких переменных
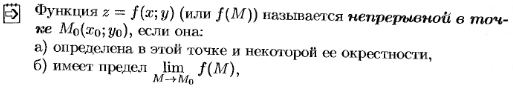
27. Частные производные. Геометрический смысл частных производных функции двух переменных.
Частной
производной по переменной х
функции
в точке
называется предел
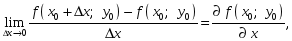(18.1)
если он существует.
Производную (18.1)
обозначают также
Если частные
производные определены на множестве
и
то они являются функциями двух переменных
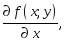
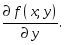
Для функции трех
переменных
в случае их существования, аналогично
определяют три частные производные
Геометрически,
частная производная является производной
по направлению одной из координатных
осей. Частная производная функции f в
точке
по
координате xk равна производной
по направлению
где единица стоит на k-ом месте.
28. Дифференцируемость функции нескольких переменных.
!!!!!!!!!!!!!!!!!!!Функция
дифференцируема, если полное приращение
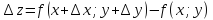можно представить в виде:
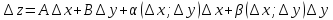
Где
A
и B
не зависят от
.
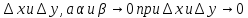Также,
компактно:
;
,
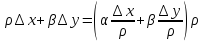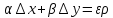где
.
!!!!!!!!!!!!!!!!!
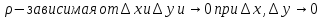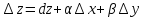
Согласно
общему определению функция
двух переменных x,y является дифференцируемой
в точке (x0,y0) своей области определения
M, если существуют такие константы a,b и
c, что для любой точки (x,y) области M верно
при этом число a неизбежно равно значению функции в точке (x0,y0), а числа b и c являются частными производными функции в той же точке, то есть
При этом всякая дифференцируемая в точке (x0,y0) функция имеет в этой точке обе частные производные, но не всякая функция, имеющая обе частные производные является дифференцируемой. Более того, существование частных производных в некоторой точке не гарантирует даже непрерывность функции в этой точке. Напр., функция
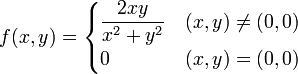
которая имеет в точке O = (0,0) обе частные производные, но не является в этой точке непрерывной. В самом деле,
и если {an} — бесконечно малая последовательность, то
поэтому предел
не существует.
График функции y = f(x,y) представляет собой поверхность в пространстве Oxyz, а график линейной функции доставляет касательную плоскость к этой поверхности, проведенную в точке (x0,y0).