
- •1. Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы.
- •3. Докажите следующее утверждение. Пусть s и s – минимальная и максимальная суммы элементов столбцов матрицы а. Тогда число Фробениуса λА матрицы а удовлетворяет неравенству s
- •5. Сформулируйте и докажите первый критерий продуктивности
- •6. Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1
- •7. Сформулируйте определение запаса продуктивности неотрицательной матрицы. Выведите формулу для вычисления запаса продуктивности через число Фробениуса.
- •9. Приведите примеры задач лп на минимум (задача о диете) и на максимум (задача об использовании ресурсов)
- •10. Приведите общую постановку злп. Дайте определения следующим терминам: целевая ф-ия, допустимое мн-во задачи, оптимальное решение, оптимальное мн-во.
- •26.Приведите пример двух взаимно двойственных задач лп. Сформулируйте правило построения двойственной задачи.
- •27. Сформулируйте и докажите основное неравенство для взаимно двойственных задач лп. Сформулируйте достаточный признак оптимальности.
- •28. Сформулируйте первую и вторую теоремы двойственности. Докажите вторую теорему двойственности (теорему равновесия)
- •29. Приведите пример постановки транспортной задачи. Что такое оптимальный план перевозок? Что такое транспортная задача с правильным балансом? Сформулируйте критерий разрешимости транспортной задачи.
- •30. Опишите методы построения начального опорного плана транспортной задачи (метод северо-западного угла, метод минимального тарифа.
- •38. Опишите модель Самуэльсона-Хикса. Какие экономические предположения лежат в ее основе? Запишите уравнение Хикса. В каком случае решением уравнения Хикса является стационарная последовательность?
- •39. Опишите паутинную модель рынка. Какие экономические предположения лежат в ее основе? Найдите равновесное состояние паутинной модели рынка.
26.Приведите пример двух взаимно двойственных задач лп. Сформулируйте правило построения двойственной задачи.
Пусть дана задача ЛП:
f = 74x1 + 106x2 + 20x3 → min,
− 6x1
+ 10x2 −
4x3
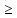 6, (1)
6, (1)
− 4x1 − 2x2 + 6x3
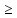 4,
4,
x1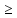 0, x2
0, x2
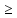 0, x3
0, x3
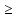 0.
0.
Составим задачу, двойственную (1), следуя обычному правилу:
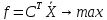
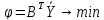
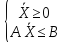
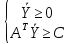
Поскольку в исходной задаче целевая функция исследуется на минимум, двойственная задача представляет собой задачу на максимум. Количество нетривиальных ограничений исходной задачи равно количеству неизвестных двойственной задачи, так что в двойственной задаче будет фигурировать 2 неизвестных z1, z2. Коэффициенты целевой функции ϕ двойственной задачи равны правым частям ограничений исходной задачи:
ϕ = 6z1 + 4z2 → max
Количество неизвестных исходной задачи равно количеству нетривиальных огра ничений двойственной задачи, так что двойственная задача будет содержать 3 нетривиальных ограничения; матрица левых частей ограничений получается из соответствующей матрицы исходной задачи транспонированием, а правые части ограничений в двойственной задаче равны коэффициентам целевой функции исходной задачи:
−6z1 − 4z2
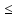 74,
74,
10z1 − 2z2
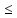 106,
106,
−4z1 + 6z2
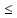 20.
20.
Таким образом, двойственная задача имеет вид:
ϕ = 6z1 + 4z2 → max,
−6z1 − 4z2
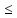 74,
74,
10z1 − 2z2
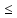 106,
106,
−4z1 + 6z2
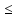 20,
20,
z1
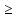 0, z2
0, z2
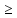 0.
0.
27. Сформулируйте и докажите основное неравенство для взаимно двойственных задач лп. Сформулируйте достаточный признак оптимальности.
I.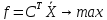 II.
II.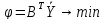
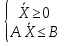
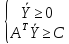
Пусть Х – какое–нибудь допустимое решение задачи 1, а У – какое-нибудь допустимое решение задачи 2. Тогда f(X)≤φ(Y)
Доказательство: Имеем AX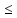 B,
откуда следует (AX)T
B,
откуда следует (AX)T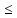 BT.
Умножив обе части этого нер-ва справа
на матрицу Y
BT.
Умножив обе части этого нер-ва справа
на матрицу Y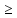 0,
получим (XTAT)Y
0,
получим (XTAT)Y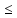 BTY
или, ввиду ассоциативности умножения
матриц, XT(ATY)
BTY
или, ввиду ассоциативности умножения
матриц, XT(ATY)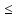 BTY=
BTY=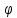 (Y).
Аналогично имеем ATY
(Y).
Аналогично имеем ATY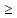 C,
умножив обе части слева на матрицу XT
C,
умножив обе части слева на матрицу XT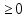 ,
будем иметь XT(ATY)
,
будем иметь XT(ATY)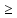 XTC=f(X).
Соединяя два полученных неравенства,
можем записать f(X)
XTC=f(X).
Соединяя два полученных неравенства,
можем записать f(X)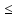 XTATY
XTATY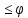 (Y).
Отсюда и следует основное неравенство.
(Y).
Отсюда и следует основное неравенство.
Достаточный признак оптимальности.
Если для каких-то допустимых решений
Х0 Y0 задач I
и II выполняется равенство
f(X0)=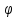 (Y0),
то X0 есть оптимальное
решение задачи I, а Y0
– оптимальное решение задачи II.
(Y0),
то X0 есть оптимальное
решение задачи I, а Y0
– оптимальное решение задачи II.
28. Сформулируйте первую и вторую теоремы двойственности. Докажите вторую теорему двойственности (теорему равновесия)
1 теорема двойственности. Критерий
оптимальности. Если разрешима одна из
двойственных задач I или
II, то разрешима и другая,
причем maxf=min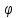 .
.
Пусть X и Y
– допустимые решения задачи I
и II соответственно. Для
того, чтобы X было оптимальным
решением задачи II,
необходимо и достаточно выполнение
равенства f(X)=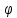 (Y)
(Y)
2 теорема двойственности. Теорема
равновесия. Оптимальные решения
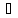 *=(х1*,х2*,…хn*)Т
и ŷ*=(у1*,у2*,…,уn*)
пары двойственных задач связаны следующим
соотношением:
*=(х1*,х2*,…хn*)Т
и ŷ*=(у1*,у2*,…,уn*)
пары двойственных задач связаны следующим
соотношением:
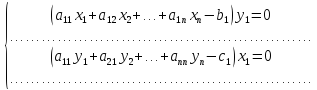 (1)
(1)
Доказательство: Из критерия оптимальности
=>
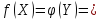
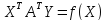
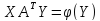
Пусть задача 1 имеет размеры m*n
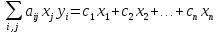
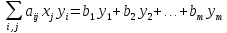
Где i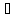 [1;m],
j
[1;m],
j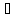 [1;n]
[1;n]
x1(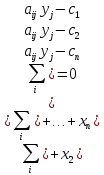
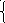
y1(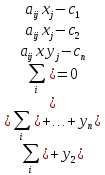
Что и записано в системе (1). ЧТД
29. Приведите пример постановки транспортной задачи. Что такое оптимальный план перевозок? Что такое транспортная задача с правильным балансом? Сформулируйте критерий разрешимости транспортной задачи.
Пусть имеются m поставщиков A1,A2,...,Am и n потребителей B1,B2,...,Bn некоторого однородного продукта. Для i-го поставщика задан объем производства ai ≥ 0 (i= (1;m)), а для j-го потребителя — объем потребления bj ≥0 (j= (1;n)) и известна стоимость доставки единицы продукта cij≥0 из пункта производства i в пункт потребления j. Переменные xij≥0 характеризуют объем первозки между i-м поставщиком и j-м потребителем. Оптимальный план транспортировки соответствует минимуму линейной целевой функции
F(X) = mi=1∑nj=1∑cij xij→min при ограничениях на потребление и поставку mi=1∑xij=bj , nj=1∑xij=ai . Число базисных переменных в системе ограничений равно m+n-1.
Данные обычно представляют в виде транспортной таблицы:
|
Поставщики |
Потребители |
Запасы |
||||
|
B1 |
B2 |
... |
Bn |
|||
|
A1 |
С11 x11 |
С12 x12 |
... |
С1n x1n |
a1 |
|
|
A2 |
С21 x21 |
С22 x22 |
... |
С23 x23 |
a2 |
|
|
... |
... |
... |
... |
... |
... |
|
|
Am |
Сm1 xm1 |
Сm2 xm2 |
... |
Сmn xmn |
an |
|
|
Потребности |
b1 |
b2 |
... |
bn |
|
|
Критерий разрешимости транспортной задачи — транспортная задача разрешима только, если она имеет правильный баланс.
Общее количество товара у поставщиков равно mi=1∑ai , a общая потребность в товаре в пунктах назначения есть nj=1∑bj , . Если mi=1∑ai = nj=1∑bj , т. е. суммарные запасы поставщиков равны суммарным запросам потребителей, то такая задача называется задачей с правильным балансом, а ее модель — закрытой.
