5. Уравнения равновесия твердого тела под действием плоской системы параллельных сил

(начало в билете 4)

В частном случае, если все силы плоской системы параллельны, то условия равновесия таких сил выражаются не тремя, а двумя уравнениями:

Fiy = 0; MO(Fi) = 0

причем ось Ох параллельна данным силам.

6. Центр параллельных сил. Координаты центра параллельных сил

Центр параллельных сил, точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол. Координаты Центр параллельных сил определяются формулами:

где xk, yk, zk - координаты точек приложения сил. Понятием Центр параллельных сил пользуются при отыскании координат центров тяжести

7. Координаты центра тяжести однородного тела

8. Матрица жесткости плоского стержня в местной системе координат

Каждый стержень в конструкции имеет свою ориентацию. Поэтому при расчете вводится понятие местной, или локальной (связанной с осью стержня) и общей для всей конструкции систем координат.

На рис. 1 xi'-yi' - местная, а х -у - общая система координат. Начальный узел конечного элемента обозначен через "н", конечный узел - через "к".

В общем виде матрицу Ri' можно представить следующим образом:

Каждый коэффициент матрицы R'i имеет определенный физический смысл. Произвольный элемент rјi' матрицы Ri' численно равен i-ой составляющей реакции в узловой точке от единичного смещения по j-му направлению.

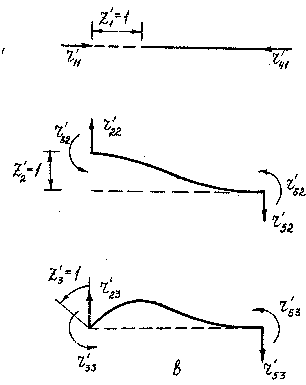
Элементы первого столбца матрицы (1) - реакции на концах стержня от смещения Z1' =1 (см. рис. 2в). Второй и третий столбцы - реакции от смещения Z2' = 1 и от смещения Z 3' =1, показанных на том же рисунке. Элементы трех последних столбцов определяются смещениями правого конца стержня.

Устанавливается следующее правило знаков : положительная реакция совпадает с положительным направлением соответствующего перемещения и наоборот.

Полученная таким образом матрица имеет вид:

Где Е - модуль упругости материала; F и J - площадь и момент инерции поперечного сечения. Длина конечного элемента l в матрице (2) подсчитывается по формуле:

где хн, yн и хк,ук - координаты соответственно начального и конечного узлов конечного элемента.

Матрицу (2) можно записать в сокращенном виде, разделив ее на четыре блока размерностью 3х3:

Каждый блок в (3) представляет собой матрицу реакций, возникающих в начале и конце стержня, что отмечено соответственно буквами "н" и "к". Вторая буква индекса указывает, смещением каких связей - начальных ли конечных - вызваны эти реакции. Например, R 'кн - это блок реакций на конце на конце от смещения связей в начале стержня.